人教版(新)七上-1.4.2 有理数的除法 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-1.4.2 有理数的除法 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:27:48 | ||
图片预览










文档简介
(共34张PPT)
1.4.2 有理数的除法
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
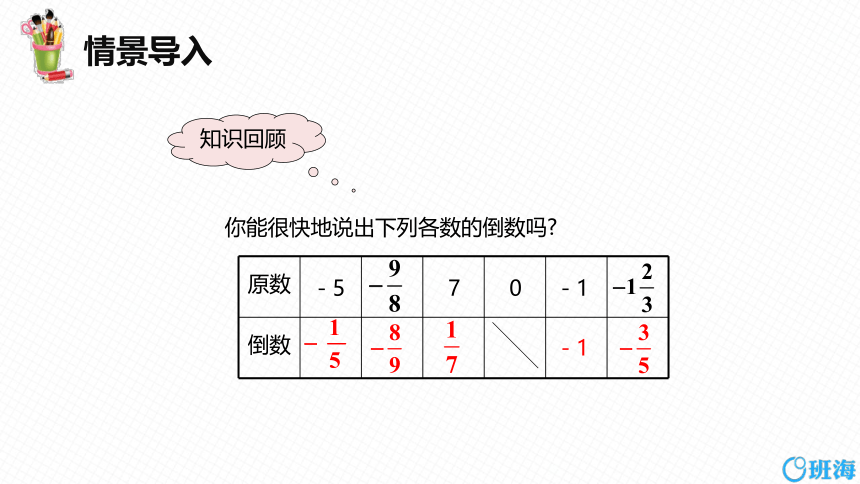
知识回顾
你能很快地说出下列各数的倒数吗
原数
倒数
-1
7
-1
-5
0
新课精讲
探索新知
1
知识点
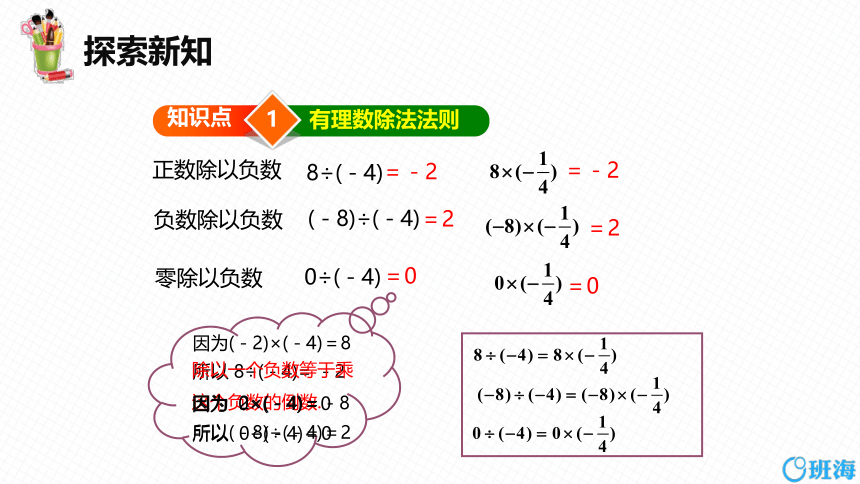
有理数除法法则
正数除以负数
负数除以负数
零除以负数
8÷(-4)
(-8)÷(-4)
0÷(-4)
因为(-2)×(-4)=8
所以 8÷(-4)= -2
除以一个负数等于乘这个负数的倒数.
=-2
=2
=0
=-2
=2
=0
因为 2×(-4)=-8
所以(-8)÷(-4)=2
因为 0×(-4)=0
所以 0÷(-4)=0
探索新知
有理数除法法则:
除以一个不等于0的数,等于乘这个数的倒数.
探索新知
两数相除, 同号得 , 异号得 ,
并把绝对值相 , 0除以任何一个不等于0的数,
都得 .
正
负
除
0
两数相除的符号法则:
探索新知
例1 (1)(-18)÷6;
(2)(-27)÷(-9);
解:(1)原式=(-18)×
(2)原式=(-27)×
探索新知
总 结
有理数除法的一般步骤:
(1)确定商的符号;(2)把除数化为它的倒数;(3)利用乘法计算结果.
1.-2的倒数是( )
A.2 B.-2 C. D.-
2.下列计算中错误的是( )
A. (-5)÷ =(-5)×(-2)
B. ÷(-3)=3×(-3)
C.(-2)÷(-3)=(-2)×
D.
典题精讲
D
B
典题精讲
3.
A. B. C. 2 D.-2
4.下列计算正确的是( )
A
C
探索新知
2
知识点
化简分数
法则①:除以一个不等于0的数,等于乘这个数的倒数.
法则②:两数相除,同号得正,异号得负,并把绝对值相除.
特殊的:0除以任何一个不等于0的数,都得0.
探索新知
例2
若两个有理数的商是正数,和为负数,则这两个数( )
A.一正一负 B.都是正数
C.都是负数 D.不能确定
导引:若商为正数,则这两个数同号,又因为和为负数,所
以这两个数都是负数.
C
探索新知
总 结
有理数的运算法则直接运用进行有理数的运算,逆用时主要是判断符号的规律.特别注意答案的多样性.
探索新知
例3 计算:
(1)(-42)÷(-6) (2)(-12)÷
(3) (4)0÷(-3.72)
(5)1÷(-1.5) (6)(-4.7)÷1
导引:(1)运用法则②,同号得正,先定符号,再算对值. (2)运用法则①,除号变乘号,除数变为它的倒数. (3)带分数化为假分数再相除. (4)0除以任何一个不为0的数都等于0. (5)小数化为分数再相除. (6)任何数除以1都等于它本身.
探索新知
解: (1)(-42)÷(-6)=7.
(2)(-12)÷
(3)
(4)0÷(-3.72)=0.
(5)1÷(-1.5)=1÷
(6)(-4.7)÷1=-4.7.
探索新知
总 结
在进行有理数的除法运算时,要根据题目的特点,恰当地选择有理数除法法则;当能整除时,往往采用法则②直接除;当不能整除,特别是当除数是分数时,往往采用法则①,把除法转化为乘法再计算.
典题精讲
1.下列关系不成立的是( )
A. B.
C. D.
D
2.若两个有理数的商是负数,那么这两个数一定 ( )
A.都是正数 B.都是负数 C.符号相同 D.符号不同
3.两个有理数的商是正数,则( )
A.它们的和为正数 B.它们的和为负数
C.至少有一个数为正数 D.它们的积为正数
C
D
探索新知
3
知识点
有理数的乘除混合运算
有理数的乘除混合运算:
方法①:有理数的乘法、除法是同级运算,在混合运算中,
应该从左向右依次计算,有括号的先算括号里的,
再算括号外的.
方法②:有理数的乘除混合运算,也可以先把除法转化为
乘法,然后根据有理数乘法法则计算.
探索新知
例4 计算:
(1) (2)
解:
探索新知
总 结
因为有理数的除法可以化为乘法,所以可以利用乘法的运算性质简化运算. 乘除混合运算往往先将除法化成乘法,然后确定积的符号,最后求出结果.
典题精讲
1.下列运算正确的是( )
A.
B.
C.
D.
C
2.计算 的结果是( )
A. 1 B.5
C. 25 D.
3.计算 的结果是( )
A. B.
C. D.
典题精讲
C
B
学以致用
小试牛刀
1.有理数除法法则:除以一个不等于0的数,等于乘这个数的
________,即a÷b=a ______(b______).
2.两数相除,同号得________,异号得________,并把绝对值
________.0除以任何一个______________,都得________.
倒数
≠0
正
负
相除
不等于0的数
0
3.分数线具有除号的作用,因此化简分数时可以将分数看成
分子除以分母,利用_________法则进行化简.
4.分数的符号法则:分数的分子、分母及分数本身的符号,
改变其中任意两个,分数值__________.
除法
不变
小试牛刀
5.(-21)÷7的结果是( )
A.3 B.-3 C. D.-
B
6.若x (-3)= ,则x等于( )
A. B.- C. D.-
B
7.根据有理数的除法法则,下列各项不成立的是( )
A. = = B.- = =
C. = D.若a>b, <0,则a<0
D
小试牛刀
8.点A,B在数轴上的位置如图所示,其对应的数分别是a和b.
对于以下结论:
甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ba≥0. 其中
正确的是( )
A.甲、乙 B.丙、丁
C.甲、丙 D.乙、丁
C
小试牛刀
9.计算:
(1) (-3.5)÷ × (2) ÷ ×
解:
解:
小试牛刀
10.有理数a在数轴上对应点的位置如图所示,请比较a,
,-a,- 的大小,并用“<”号连接.
解:小试牛刀
11.若规定:a△b= ÷ ,例如:2△3= ÷ =
- ,试求(2△7)△4的值.
2△7= ÷ = ,
△4= ÷ = ,
所以(2△7)△4的值为 .
解:
课堂小结
课堂小结
做有理数的除法运算要注意三点:
(1)0不能作除数;
(2)无论是直接除还是转化成乘法,都要先确定商的符号;
(3)被除数或除数中的小数一般需化成分数;带分数一定要化成假分数.
有理数的除法的运算方法:
当两数不能整除或除数是分数时,用法则1,把除法运算转化为乘法运算;当两数能整除时用法则2,直接相除,相除时先确定商的符号,再确定商的绝对值.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.4.2 有理数的除法
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
知识回顾
你能很快地说出下列各数的倒数吗
原数
倒数
-1
7
-1
-5
0
新课精讲
探索新知
1
知识点
有理数除法法则
正数除以负数
负数除以负数
零除以负数
8÷(-4)
(-8)÷(-4)
0÷(-4)
因为(-2)×(-4)=8
所以 8÷(-4)= -2
除以一个负数等于乘这个负数的倒数.
=-2
=2
=0
=-2
=2
=0
因为 2×(-4)=-8
所以(-8)÷(-4)=2
因为 0×(-4)=0
所以 0÷(-4)=0
探索新知
有理数除法法则:
除以一个不等于0的数,等于乘这个数的倒数.
探索新知
两数相除, 同号得 , 异号得 ,
并把绝对值相 , 0除以任何一个不等于0的数,
都得 .
正
负
除
0
两数相除的符号法则:
探索新知
例1 (1)(-18)÷6;
(2)(-27)÷(-9);
解:(1)原式=(-18)×
(2)原式=(-27)×
探索新知
总 结
有理数除法的一般步骤:
(1)确定商的符号;(2)把除数化为它的倒数;(3)利用乘法计算结果.
1.-2的倒数是( )
A.2 B.-2 C. D.-
2.下列计算中错误的是( )
A. (-5)÷ =(-5)×(-2)
B. ÷(-3)=3×(-3)
C.(-2)÷(-3)=(-2)×
D.
典题精讲
D
B
典题精讲
3.
A. B. C. 2 D.-2
4.下列计算正确的是( )
A
C
探索新知
2
知识点
化简分数
法则①:除以一个不等于0的数,等于乘这个数的倒数.
法则②:两数相除,同号得正,异号得负,并把绝对值相除.
特殊的:0除以任何一个不等于0的数,都得0.
探索新知
例2
若两个有理数的商是正数,和为负数,则这两个数( )
A.一正一负 B.都是正数
C.都是负数 D.不能确定
导引:若商为正数,则这两个数同号,又因为和为负数,所
以这两个数都是负数.
C
探索新知
总 结
有理数的运算法则直接运用进行有理数的运算,逆用时主要是判断符号的规律.特别注意答案的多样性.
探索新知
例3 计算:
(1)(-42)÷(-6) (2)(-12)÷
(3) (4)0÷(-3.72)
(5)1÷(-1.5) (6)(-4.7)÷1
导引:(1)运用法则②,同号得正,先定符号,再算对值. (2)运用法则①,除号变乘号,除数变为它的倒数. (3)带分数化为假分数再相除. (4)0除以任何一个不为0的数都等于0. (5)小数化为分数再相除. (6)任何数除以1都等于它本身.
探索新知
解: (1)(-42)÷(-6)=7.
(2)(-12)÷
(3)
(4)0÷(-3.72)=0.
(5)1÷(-1.5)=1÷
(6)(-4.7)÷1=-4.7.
探索新知
总 结
在进行有理数的除法运算时,要根据题目的特点,恰当地选择有理数除法法则;当能整除时,往往采用法则②直接除;当不能整除,特别是当除数是分数时,往往采用法则①,把除法转化为乘法再计算.
典题精讲
1.下列关系不成立的是( )
A. B.
C. D.
D
2.若两个有理数的商是负数,那么这两个数一定 ( )
A.都是正数 B.都是负数 C.符号相同 D.符号不同
3.两个有理数的商是正数,则( )
A.它们的和为正数 B.它们的和为负数
C.至少有一个数为正数 D.它们的积为正数
C
D
探索新知
3
知识点
有理数的乘除混合运算
有理数的乘除混合运算:
方法①:有理数的乘法、除法是同级运算,在混合运算中,
应该从左向右依次计算,有括号的先算括号里的,
再算括号外的.
方法②:有理数的乘除混合运算,也可以先把除法转化为
乘法,然后根据有理数乘法法则计算.
探索新知
例4 计算:
(1) (2)
解:
探索新知
总 结
因为有理数的除法可以化为乘法,所以可以利用乘法的运算性质简化运算. 乘除混合运算往往先将除法化成乘法,然后确定积的符号,最后求出结果.
典题精讲
1.下列运算正确的是( )
A.
B.
C.
D.
C
2.计算 的结果是( )
A. 1 B.5
C. 25 D.
3.计算 的结果是( )
A. B.
C. D.
典题精讲
C
B
学以致用
小试牛刀
1.有理数除法法则:除以一个不等于0的数,等于乘这个数的
________,即a÷b=a ______(b______).
2.两数相除,同号得________,异号得________,并把绝对值
________.0除以任何一个______________,都得________.
倒数
≠0
正
负
相除
不等于0的数
0
3.分数线具有除号的作用,因此化简分数时可以将分数看成
分子除以分母,利用_________法则进行化简.
4.分数的符号法则:分数的分子、分母及分数本身的符号,
改变其中任意两个,分数值__________.
除法
不变
小试牛刀
5.(-21)÷7的结果是( )
A.3 B.-3 C. D.-
B
6.若x (-3)= ,则x等于( )
A. B.- C. D.-
B
7.根据有理数的除法法则,下列各项不成立的是( )
A. = = B.- = =
C. = D.若a>b, <0,则a<0
D
小试牛刀
8.点A,B在数轴上的位置如图所示,其对应的数分别是a和b.
对于以下结论:
甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:ba≥0. 其中
正确的是( )
A.甲、乙 B.丙、丁
C.甲、丙 D.乙、丁
C
小试牛刀
9.计算:
(1) (-3.5)÷ × (2) ÷ ×
解:
解:
小试牛刀
10.有理数a在数轴上对应点的位置如图所示,请比较a,
,-a,- 的大小,并用“<”号连接.
解:
11.若规定:a△b= ÷ ,例如:2△3= ÷ =
- ,试求(2△7)△4的值.
2△7= ÷ = ,
△4= ÷ = ,
所以(2△7)△4的值为 .
解:
课堂小结
课堂小结
做有理数的除法运算要注意三点:
(1)0不能作除数;
(2)无论是直接除还是转化成乘法,都要先确定商的符号;
(3)被除数或除数中的小数一般需化成分数;带分数一定要化成假分数.
有理数的除法的运算方法:
当两数不能整除或除数是分数时,用法则1,把除法运算转化为乘法运算;当两数能整除时用法则2,直接相除,相除时先确定商的符号,再确定商的绝对值.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
