人教版(新)七上-1.5.2 科学计数法【优质课件】
文档属性
| 名称 | 人教版(新)七上-1.5.2 科学计数法【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:27:48 | ||
图片预览











文档简介
(共33张PPT)
1.5.2 科学计数法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
有一个故事,说的是一个财主的孩子不爱学习,财主把他送到学堂,说学会计帐就行了,于是老师只教他写数字,第一天教个“一”,第二天是“二”,第三天是“三”. 第四天这个孩子不上学了,财主问他儿子怎么不去了,他儿子说他学会了. 于是财主叫他记帐,第一天就忙坏他了,因为两个欠帐人的名字是“千百万”和“万百千”,于是那个笨孩子就用梳子按着写.
如果要你书写生活中的大数,你会怎么办?
新课精讲
1
知识点
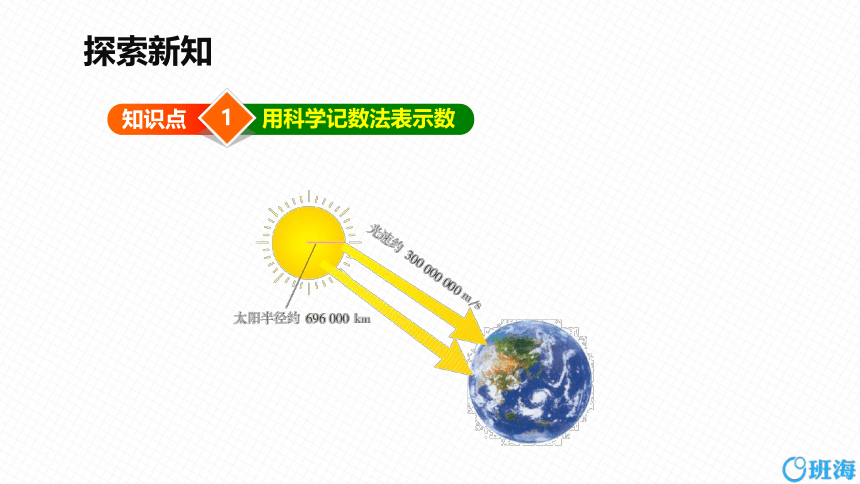
用科学记数法表示数
探索新知
探索新知
世界总人口数约为
7 000 000 000人.
探索新知
696 000
300 000 000
700 000 000
有简单的表示方法吗?
探索新知
10的乘方有如下的特点:
一般地,10的n次幂等于10···0(在1的后面有n个0),所以就可以用10的乘方表示一些大数.
你知道
分别等于多少吗?
的意义和规律是什么?
探索新知
书写简短,便于读数.
读作:5.67乘10的8次方(幂)
例如:567 000 000
22 600 000 000 = 2.26×10 000 000 000 = 2.26×
6 100 000 000= 6.1×1 000 000 000
=6.1×109
= 5.67×100 000 000
= 5.67×
探索新知
1.科学记数法:把一个大于10的数表示成a×10n的形式(其中a大于
或等于1且小于10,n是正整数),对于小于-10的数也可以类似
表示.
2.科学记数法中a与n的确定:
(1)a就是把原数的小数点移动到左边第1个不是0的数字后面所
得到的数;
(2)n的值比原数的整数位数少1.
探索新知
1 000 000=106,
57 000 000 = 5. 7 ×107,
-123 000 000 000 = -1.23×1011.
例1 用科学记数法表示下列各数:
1 000 000,
57 000 000,
-123 000 000 000.
探索新知
导引:根据科学记数法的概念:先把1.62亿写成162 000 000,
再确定a的值和n的值.1.62亿=162 000 000=1.62×108,
故选C.
例2 移动互联网已经全面进入人们的日常生活.截止2015年3月,
全国4G用户总数为1.62亿,其中1.62亿用科学记数法表示为
( )
A.1.62×104 B.162×106
C.1.62×108 D.0.162×109
C
探索新知
总 结
把一个数写成a×10n的形式(其中,1≤|a| <10,n为整数),这种记数的方法叫做科学记数法.其方法是:(1)确定a,a是只有一位整数的数;(2)确定n,当原数的绝对值≥10时,n为正整数,且等于原数的整数位数减1.
典题精讲
1.将一个数用科学记数法表示为a×10n的形式中,n是整数,|a|的
取值范围是( )
A.1<|a|<10 B.1<|a|≤10
C.1≤|a|<10 D.1≤|a|≤10
2.数361 000 000用科学记数法表示,以下正确的是( )
A.0.361×108 B.3.61×108
C.3.61×107 D.36.1×107
C
B
典题精讲
3.截至2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力
达到140 000 立方米,将140 000用科学记数法表示应为( )
A.14×104 B.1.4×105
C.1.4×106 D.0.14×106
B
4.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,
根据规划“一带一路”地区覆盖总人口约为4 400 000 000人,这
个数用科学记数法表示为( )
A.44×108 B.4.4×109
C.4.4×108 D.4.4×1010
B
探索新知
2
知识点
写出用科学记数法表示的数的原数
还原方法:
把科学记数法表示的数a×10n还原成原数时,只需把a中的
小数点向右移动n位,并去掉乘号和10n即可,若向右移动的位
数不够,应用0补足.
探索新知
例3 下列求原数不正确的是( )
A.3.56×104=35 600
B.-4.67×106=-4 670 000
C.2×102=200
D.3×105=30 000
导引:用科学记数法表示为a×10n的数,其原数等于把a的小数
点向右移动n位后得到的数,若向右移动的位数不够,应
用0补足,显然3×105=300 000.
D
探索新知
总 结
将绝对值较大的数用科学记数法表示成a×10n时,其中1≤|a|<10, n等于这个数的整数位数减1.
探索新知
例4 比较大小:9.523×1010与1.002×1011.
导引:可先写出原数,再比较大小.
解:9.523×1010=95 230 000 000,
1.002×1011=100 200 000 000,
因为95 230 000 000<100 200 000 000,
所以9.523×1010<1.002×1011.
探索新知
总 结
比较用科学记数法表示的两个正数的大小时,常用的方法:先看n,n大的原数就大;若n相同,则a越大,原数越大.类似地,比较用科学记数法表示的两个负数的大小时,常用的方法:先看n,n大的原数就小;若n相同,|a|大的原数反而小.
典题精讲
1.用科学记数法表示一个六位整数,则a×10n中n= ;若一个数用科学记数法表示为a×107,则这个数是 位数.
2.把下列用科学记数法表示的数写成原来的形式:
105= ; 6.32×103= ;
-7.254×102= ;
-2.1×104= .
5
八
100000
6320
-725.4
-21000
典题精讲
3.5.17×10n+1是用科学记数法表示的数,则它的原数是
( )位整数.
A. n-1
B. n
C. n+1
D. n+2
D
学以致用
小试牛刀
1.一般地,一个绝对值大于10的数可以表示成_______的形式(其中
a的绝对值大于或等于_____且小于____,n是正整数),这种记数
方法叫做__________________.
a×10n
1
10
科学记数法
2.把用科学记数法表示的数a×10n(n是正整数)还原成原数时,只
需把a中的小数点向______移动______位,并去掉乘号和10n即
可;若向右移动的位数不够,应用0补足.
右
n
小试牛刀
3.随着“一带一路”建设的不断发展,我国已与多个国家建立了
经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达
8200000 t.将8200000用科学记数法表示为( )
A.8.2×105 B.82×105
C.8.2×106 D.82×107
C
小试牛刀
4.下列各式不正确的是( )
A.3.56×104=35600 B.-4.67×106=-4670000
C.2×102=200 D.3×105=30 000
D
5.为了实现街巷硬化工程高质量“全覆盖”,某省2018年1~4
月公路建设累计投资9.27×109元,也就是投资了( )
A.92.7亿元 B.9.27亿元
C.927亿元 D.0.927亿元
A
小试牛刀
6.先计算,然后根据计算结果回答问题:
(1)计算:
①(1×102)×(2×104)=________;
②(2×104)×(3×107)=________;
③(3×107)×(4×104)=__________;
④(4×105)×(5×1010)=________.
2×106
6×1011
1.2×1012
2×1016
小试牛刀
(2)已知式子(a×10n)×(b×10m)=c×10p成立,其中a,b,c均
为大于或等于1而小于10的数,m,n,p均为正整数.你能
写出m,n,p之间存在的等量关系吗?
若ab<10,则p=m+n;
若ab≥10,则p=m+n+1.
小试牛刀
7.如果规定:0.1= =10-1,0.01= =10-2,0.001
= =10-3.
(1) 你能用10的指数的形式表示0.000 1,0.000 01吗?
(2) 你能将0.001 768表示成a×10n的形式吗(其中1≤|a|<10,
n为负整数)
解:(1) 0.000 1= =10-4,0.000 01= =10-5.
(2) 0.001 768=1.768×10-3.
课堂小结
课堂小结
1.用科学记数法表示绝对值较大的数:
把一个绝对值大于10的数表示成a×10n(1≤|a|<10,n是正整数)的形式,其中a的整数位数为1,数的正负符号不变,n为原数的整数位数减1.
说明:科学记数法只改变数的书写形式,不改变数的大小.
2.将用科学记数法表示的数还原的方法:
把一个用科学记数法表示的数还原为原数时,只需将小数点向右移动n位(不足的数位用0补齐),并把10n去掉即可.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.5.2 科学计数法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
有一个故事,说的是一个财主的孩子不爱学习,财主把他送到学堂,说学会计帐就行了,于是老师只教他写数字,第一天教个“一”,第二天是“二”,第三天是“三”. 第四天这个孩子不上学了,财主问他儿子怎么不去了,他儿子说他学会了. 于是财主叫他记帐,第一天就忙坏他了,因为两个欠帐人的名字是“千百万”和“万百千”,于是那个笨孩子就用梳子按着写.
如果要你书写生活中的大数,你会怎么办?
新课精讲
1
知识点
用科学记数法表示数
探索新知
探索新知
世界总人口数约为
7 000 000 000人.
探索新知
696 000
300 000 000
700 000 000
有简单的表示方法吗?
探索新知
10的乘方有如下的特点:
一般地,10的n次幂等于10···0(在1的后面有n个0),所以就可以用10的乘方表示一些大数.
你知道
分别等于多少吗?
的意义和规律是什么?
探索新知
书写简短,便于读数.
读作:5.67乘10的8次方(幂)
例如:567 000 000
22 600 000 000 = 2.26×10 000 000 000 = 2.26×
6 100 000 000= 6.1×1 000 000 000
=6.1×109
= 5.67×100 000 000
= 5.67×
探索新知
1.科学记数法:把一个大于10的数表示成a×10n的形式(其中a大于
或等于1且小于10,n是正整数),对于小于-10的数也可以类似
表示.
2.科学记数法中a与n的确定:
(1)a就是把原数的小数点移动到左边第1个不是0的数字后面所
得到的数;
(2)n的值比原数的整数位数少1.
探索新知
1 000 000=106,
57 000 000 = 5. 7 ×107,
-123 000 000 000 = -1.23×1011.
例1 用科学记数法表示下列各数:
1 000 000,
57 000 000,
-123 000 000 000.
探索新知
导引:根据科学记数法的概念:先把1.62亿写成162 000 000,
再确定a的值和n的值.1.62亿=162 000 000=1.62×108,
故选C.
例2 移动互联网已经全面进入人们的日常生活.截止2015年3月,
全国4G用户总数为1.62亿,其中1.62亿用科学记数法表示为
( )
A.1.62×104 B.162×106
C.1.62×108 D.0.162×109
C
探索新知
总 结
把一个数写成a×10n的形式(其中,1≤|a| <10,n为整数),这种记数的方法叫做科学记数法.其方法是:(1)确定a,a是只有一位整数的数;(2)确定n,当原数的绝对值≥10时,n为正整数,且等于原数的整数位数减1.
典题精讲
1.将一个数用科学记数法表示为a×10n的形式中,n是整数,|a|的
取值范围是( )
A.1<|a|<10 B.1<|a|≤10
C.1≤|a|<10 D.1≤|a|≤10
2.数361 000 000用科学记数法表示,以下正确的是( )
A.0.361×108 B.3.61×108
C.3.61×107 D.36.1×107
C
B
典题精讲
3.截至2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力
达到140 000 立方米,将140 000用科学记数法表示应为( )
A.14×104 B.1.4×105
C.1.4×106 D.0.14×106
B
4.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,
根据规划“一带一路”地区覆盖总人口约为4 400 000 000人,这
个数用科学记数法表示为( )
A.44×108 B.4.4×109
C.4.4×108 D.4.4×1010
B
探索新知
2
知识点
写出用科学记数法表示的数的原数
还原方法:
把科学记数法表示的数a×10n还原成原数时,只需把a中的
小数点向右移动n位,并去掉乘号和10n即可,若向右移动的位
数不够,应用0补足.
探索新知
例3 下列求原数不正确的是( )
A.3.56×104=35 600
B.-4.67×106=-4 670 000
C.2×102=200
D.3×105=30 000
导引:用科学记数法表示为a×10n的数,其原数等于把a的小数
点向右移动n位后得到的数,若向右移动的位数不够,应
用0补足,显然3×105=300 000.
D
探索新知
总 结
将绝对值较大的数用科学记数法表示成a×10n时,其中1≤|a|<10, n等于这个数的整数位数减1.
探索新知
例4 比较大小:9.523×1010与1.002×1011.
导引:可先写出原数,再比较大小.
解:9.523×1010=95 230 000 000,
1.002×1011=100 200 000 000,
因为95 230 000 000<100 200 000 000,
所以9.523×1010<1.002×1011.
探索新知
总 结
比较用科学记数法表示的两个正数的大小时,常用的方法:先看n,n大的原数就大;若n相同,则a越大,原数越大.类似地,比较用科学记数法表示的两个负数的大小时,常用的方法:先看n,n大的原数就小;若n相同,|a|大的原数反而小.
典题精讲
1.用科学记数法表示一个六位整数,则a×10n中n= ;若一个数用科学记数法表示为a×107,则这个数是 位数.
2.把下列用科学记数法表示的数写成原来的形式:
105= ; 6.32×103= ;
-7.254×102= ;
-2.1×104= .
5
八
100000
6320
-725.4
-21000
典题精讲
3.5.17×10n+1是用科学记数法表示的数,则它的原数是
( )位整数.
A. n-1
B. n
C. n+1
D. n+2
D
学以致用
小试牛刀
1.一般地,一个绝对值大于10的数可以表示成_______的形式(其中
a的绝对值大于或等于_____且小于____,n是正整数),这种记数
方法叫做__________________.
a×10n
1
10
科学记数法
2.把用科学记数法表示的数a×10n(n是正整数)还原成原数时,只
需把a中的小数点向______移动______位,并去掉乘号和10n即
可;若向右移动的位数不够,应用0补足.
右
n
小试牛刀
3.随着“一带一路”建设的不断发展,我国已与多个国家建立了
经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达
8200000 t.将8200000用科学记数法表示为( )
A.8.2×105 B.82×105
C.8.2×106 D.82×107
C
小试牛刀
4.下列各式不正确的是( )
A.3.56×104=35600 B.-4.67×106=-4670000
C.2×102=200 D.3×105=30 000
D
5.为了实现街巷硬化工程高质量“全覆盖”,某省2018年1~4
月公路建设累计投资9.27×109元,也就是投资了( )
A.92.7亿元 B.9.27亿元
C.927亿元 D.0.927亿元
A
小试牛刀
6.先计算,然后根据计算结果回答问题:
(1)计算:
①(1×102)×(2×104)=________;
②(2×104)×(3×107)=________;
③(3×107)×(4×104)=__________;
④(4×105)×(5×1010)=________.
2×106
6×1011
1.2×1012
2×1016
小试牛刀
(2)已知式子(a×10n)×(b×10m)=c×10p成立,其中a,b,c均
为大于或等于1而小于10的数,m,n,p均为正整数.你能
写出m,n,p之间存在的等量关系吗?
若ab<10,则p=m+n;
若ab≥10,则p=m+n+1.
小试牛刀
7.如果规定:0.1= =10-1,0.01= =10-2,0.001
= =10-3.
(1) 你能用10的指数的形式表示0.000 1,0.000 01吗?
(2) 你能将0.001 768表示成a×10n的形式吗(其中1≤|a|<10,
n为负整数)
解:(1) 0.000 1= =10-4,0.000 01= =10-5.
(2) 0.001 768=1.768×10-3.
课堂小结
课堂小结
1.用科学记数法表示绝对值较大的数:
把一个绝对值大于10的数表示成a×10n(1≤|a|<10,n是正整数)的形式,其中a的整数位数为1,数的正负符号不变,n为原数的整数位数减1.
说明:科学记数法只改变数的书写形式,不改变数的大小.
2.将用科学记数法表示的数还原的方法:
把一个用科学记数法表示的数还原为原数时,只需将小数点向右移动n位(不足的数位用0补齐),并把10n去掉即可.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
