人教版(新)七上-2.2 整式的加减 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-2.2 整式的加减 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
2.2 整式的加减
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
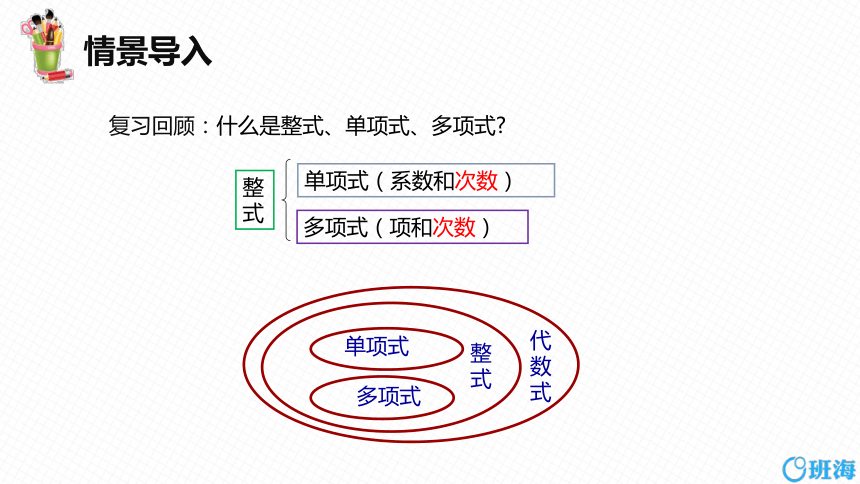
整式
单项式(系数和次数)
多项式(项和次数)
代数式
整式
单项式
多项式
复习回顾:什么是整式、单项式、多项式
新课精讲
探索新知
1
知识点
整式的加减
1. 都是整式,整式之间可以进行加减运
算,这就是整式的加减。
由于进行加减运算的整式是一个整体,所以每一个整式都
要用括号括起来。进行整式加减的一般步骤是:去括号、合并
同类项。
探索新知
例1 计算:
(1)(2x-3y)+(5x+4y) ; (2)(8a-7b)-(4a-5b).
分析:第(1)题是计算多项式2x -3y和5x+4y的和;第(2)题 是计算多项式8a-7b和4a-5b的差.
解:= 2x-3y +5x+4y
= 7x+y;
解: = 8a-7b-4a+5b
=4a-2b.
探索新知
总 结
整式的加减实质是去括号、合并同类项这两个知
识的综合.
探索新知
例2 已知A=3x2y+3xy2+y4,B=-8xy2-2x2y-2y4
求:(1)A-B;(2)A+ B.
导引:将A,B代表的多项式代入,然后去括号、合并
同类项.
解:(1)A-B=(3x2y+3xy2+y4)-(-8xy2-2x2y-2y4)
=3x2y+3xy2+y4+8xy2+2x2y+2y4
=5x2y+11xy2+3y4.
探索新知
总 结
本题的解题步骤:
(1)将A,B代表的多项式代入,特别要注意代入时将每个多项式用括号括起来;
(2)去括号;
(3)找同类项;
(4)合并同类项.
探索新知
例3 笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔
记本,2 支圆珠笔;小明买4本笔记本,3支圆珠笔.买这
些笔记本和圆珠笔,小红和小明一共花费多少钱?
解法1: 小红买笔记本和圆珠笔共花费(3x+2y)元,小明笔记本和
圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y) + (4x+3y)
= 3x+2y+4x+3y
= 7x+5y.
解法2: 小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花
费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x) + (2y+3y)
= 7x+5y.
探索新知
总 结
审清题意,在具体情境中用代数式表示数量关系,根据整式的加减的运算法则进行化简.
探索新知
例4 做大小两个长方体纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1) 做这两个纸盒共用料多少平方厘米?
(2) 做大纸盒比做小纸盒多用料多少平方厘米?
探索新知
解:小纸盒的表面积是(2ab+2bc+2ca)cm2,大纸盒的表面积是(6ab+8bc+6ca) cm2.
(1)做这两个纸盒共用料(单位:cm2)
(2ab+2bc+2ca)+ (6ab+8bc+6ca)
=2ab+2bc+2ca+ 6ab+8bc+6ca
=8ab +10bc+8ca.
(2)做大纸盒比做小纸盒多用料(单位: cm2)
(6ab+8bc+6ca)-(2ab+2bc+2ca)
= 6ab+8bc+6ca-2ab -2bc-2ca
=4ab+6bc+4ca.
探索新知
例5 某小区有一块长为40 m,宽为30 m的长方形空地现要
美化这块空地,在上面修建如图所示的十字形花圃,在
花圃内种花,其余部分种草.
(1)求花圃的面积;
(2)若建造花圃及种花的费用为每平方米100元,种草的
费用为每平方米50元,则美化这块空地共需多少元?
导引:(1)花圃面积应是两个空白长方形的面积和减去中间重合部分的正方形的面积;(2)中总费用等于建造花圃并种花的费用与种草的费用之和.
解:(1)花圃的面积为:40x+30x-x2=70x-x2(m2).
(2)美化这块空地共需:
100(70x-x2)+50[30×40-(70x-x2)]
=7 000x-100x2+60 000-3 500x+50x2
=-50x2+3 500x+60 000(元).
探索新知
总 结
在复杂的实际问题中,有的数量关系表示的整式也很复杂,需要对整式进行化简,才能求出简易的结果.
典题精讲
1.化简x+y-(x-y)的结果是( )
A.2x+2y B.2y C.2x D.0
2. 多项式3a-a2与单项式2a2的和等于( )
A.3a B.3a+a2 C.3a+2a2 D.4a2
3.化简5(2x-3)+4(3-2x)的结果为( )
A.2x-3 B.2x+9 C.8x-3 D.18x-3
B
B
A
典题精讲
5.一个单项式减去x2-y2等于x2+y2,则这个单项式是( )
A.2y2 B.-2y2 C.2x2 D.-2x2
4.若一个多项式减去-4a等于3a2-2a-1,则这个多项式是( )
A.3a2-6a-1 B.5a2-1
C.3a2+2a-1 D.3a2+6a-1
A
C
典题精讲
7.若M=3x2-5x+2,N=3x2-5x-1,则( )
A.M<N B.M=N
C.M>N D.无法确定
6.已知A=5a-3b,B=-6a+4b,则A-B等于( )
A.-a+b B.11a+b
C.11a-7b D.-a-7b
C
C
探索新知
2
知识点
求整式的值
例6
探索新知
先将式子化简,
再代入数值进行
计算比较简便.
探索新知
总 结
求整式的值时,一般是先化简(去括号、合并同类项),再把字母的值代入化简后的式子求值.
典题精讲
3.已知a2+2a=1,则整式2a2+4a-1的值是( )
A.0 B.1 C.-1 D.-2
2.已知3a-2b=2,则9a-6b=_______.
1.若多项式3x3-2x2+3x+1与多项式x2-2mx3+2x+3的
和为二次三项式,则m=________.
6
B
学以致用
小试牛刀
1.一般地,几个整式相加减,如果有括号就先__________,然
后再______________.整式加减的最后结果中不能含有同类
项,即要合并到不能再合并为止.
去括号
合并同类项
2.已知x2+2x-1=0,则3x2+6x-2=________.
1
小试牛刀
3.多项式3a2-6a+4与4a2+5a-3的差是( )
A.-a2-11a+7 B.-a2-a+1
C.a2+11a-7 D.a2-a+1
A
4.若A=x2-2xy+y2,B=x2+2xy+y2,则4xy=( )
A.A+B B.B-A
C.A-B D.2A-2B
B
小试牛刀
5.多项式(xyz2+4xy-1)+(-3xy+2z2yx-3)-(3xyz2+
xy)的值( )
A.与x,y,z的大小无关
B.与x,y的大小有关,而与z的大小无关
C.与x的大小有关,而与y,z的大小无关
D.与x,y,z的大小都有关
A
小试牛刀
6.若(A+1)2+|b-2|=0,则化简A(x2y+xy2)-b(x2y-xy2)的
结果为( )
A.3x2y B.-3x2y+xy2
C.-3x2y+3xy2 D.3x2y-xy2
B
7.若A-b=2,b-c=-3,则A-c等于( )
A.1 B.-1
C.5 D.-5
A
小试牛刀
8.先化简,再求值:2(A2b+2b3-Ab3)+3A3-(2bA2-3Ab2
+3A3)-4b3,其中A=-3,b=2.
解:原式=2a2b+4b3-2ab3+3a3-2a2b+3ab2-3a3-4b3=-2ab3+3ab2.
当a=-3,b=2时,
原式=-2×(-3)×23+3×(-3)×22=48-36=12.
小试牛刀
9.已知A+b=7,Ab=10,求(5Ab+4A+7b)+(6A-
3Ab)-(4Ab-3b)的值.
解:原式=5ab+4a+7b+6a-3ab-4ab+3b
=10(a+b)-2ab.
当a+b=7,ab=10时,
原式=10×7-2×10=50.
小试牛刀
10.当式子(2x+4)2+5取得最小值时,求式子5x-[-2x2-
(-5x+2)]的值.
解:因为当(2x+4)2+5取得最小值时,(2x+4)2=0,
所以2x+4=0,解得x=-2.
原式=5x-(-2x2+5x-2)=5x+2x2-5x+2=2x2+2.
当x=-2时,原式=2×(-2)2+2=10.
课堂小结
课堂小结
整式加减的一般步骤是:先去括号,再合并同类项.
注意:
(1)整式加减运算的过程中,一般把多项式用括号括起来;
(2)整式加减的最后结果中不能含有同类项,即要合并到不
能再合并为止.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.2 整式的加减
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
整式
单项式(系数和次数)
多项式(项和次数)
代数式
整式
单项式
多项式
复习回顾:什么是整式、单项式、多项式
新课精讲
探索新知
1
知识点
整式的加减
1. 都是整式,整式之间可以进行加减运
算,这就是整式的加减。
由于进行加减运算的整式是一个整体,所以每一个整式都
要用括号括起来。进行整式加减的一般步骤是:去括号、合并
同类项。
探索新知
例1 计算:
(1)(2x-3y)+(5x+4y) ; (2)(8a-7b)-(4a-5b).
分析:第(1)题是计算多项式2x -3y和5x+4y的和;第(2)题 是计算多项式8a-7b和4a-5b的差.
解:= 2x-3y +5x+4y
= 7x+y;
解: = 8a-7b-4a+5b
=4a-2b.
探索新知
总 结
整式的加减实质是去括号、合并同类项这两个知
识的综合.
探索新知
例2 已知A=3x2y+3xy2+y4,B=-8xy2-2x2y-2y4
求:(1)A-B;(2)A+ B.
导引:将A,B代表的多项式代入,然后去括号、合并
同类项.
解:(1)A-B=(3x2y+3xy2+y4)-(-8xy2-2x2y-2y4)
=3x2y+3xy2+y4+8xy2+2x2y+2y4
=5x2y+11xy2+3y4.
探索新知
总 结
本题的解题步骤:
(1)将A,B代表的多项式代入,特别要注意代入时将每个多项式用括号括起来;
(2)去括号;
(3)找同类项;
(4)合并同类项.
探索新知
例3 笔记本的单价是x元,圆珠笔的单价是y元.小红买3本笔
记本,2 支圆珠笔;小明买4本笔记本,3支圆珠笔.买这
些笔记本和圆珠笔,小红和小明一共花费多少钱?
解法1: 小红买笔记本和圆珠笔共花费(3x+2y)元,小明笔记本和
圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y) + (4x+3y)
= 3x+2y+4x+3y
= 7x+5y.
解法2: 小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花
费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x) + (2y+3y)
= 7x+5y.
探索新知
总 结
审清题意,在具体情境中用代数式表示数量关系,根据整式的加减的运算法则进行化简.
探索新知
例4 做大小两个长方体纸盒,尺寸如下(单位:cm):
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
(1) 做这两个纸盒共用料多少平方厘米?
(2) 做大纸盒比做小纸盒多用料多少平方厘米?
探索新知
解:小纸盒的表面积是(2ab+2bc+2ca)cm2,大纸盒的表面积是(6ab+8bc+6ca) cm2.
(1)做这两个纸盒共用料(单位:cm2)
(2ab+2bc+2ca)+ (6ab+8bc+6ca)
=2ab+2bc+2ca+ 6ab+8bc+6ca
=8ab +10bc+8ca.
(2)做大纸盒比做小纸盒多用料(单位: cm2)
(6ab+8bc+6ca)-(2ab+2bc+2ca)
= 6ab+8bc+6ca-2ab -2bc-2ca
=4ab+6bc+4ca.
探索新知
例5 某小区有一块长为40 m,宽为30 m的长方形空地现要
美化这块空地,在上面修建如图所示的十字形花圃,在
花圃内种花,其余部分种草.
(1)求花圃的面积;
(2)若建造花圃及种花的费用为每平方米100元,种草的
费用为每平方米50元,则美化这块空地共需多少元?
导引:(1)花圃面积应是两个空白长方形的面积和减去中间重合部分的正方形的面积;(2)中总费用等于建造花圃并种花的费用与种草的费用之和.
解:(1)花圃的面积为:40x+30x-x2=70x-x2(m2).
(2)美化这块空地共需:
100(70x-x2)+50[30×40-(70x-x2)]
=7 000x-100x2+60 000-3 500x+50x2
=-50x2+3 500x+60 000(元).
探索新知
总 结
在复杂的实际问题中,有的数量关系表示的整式也很复杂,需要对整式进行化简,才能求出简易的结果.
典题精讲
1.化简x+y-(x-y)的结果是( )
A.2x+2y B.2y C.2x D.0
2. 多项式3a-a2与单项式2a2的和等于( )
A.3a B.3a+a2 C.3a+2a2 D.4a2
3.化简5(2x-3)+4(3-2x)的结果为( )
A.2x-3 B.2x+9 C.8x-3 D.18x-3
B
B
A
典题精讲
5.一个单项式减去x2-y2等于x2+y2,则这个单项式是( )
A.2y2 B.-2y2 C.2x2 D.-2x2
4.若一个多项式减去-4a等于3a2-2a-1,则这个多项式是( )
A.3a2-6a-1 B.5a2-1
C.3a2+2a-1 D.3a2+6a-1
A
C
典题精讲
7.若M=3x2-5x+2,N=3x2-5x-1,则( )
A.M<N B.M=N
C.M>N D.无法确定
6.已知A=5a-3b,B=-6a+4b,则A-B等于( )
A.-a+b B.11a+b
C.11a-7b D.-a-7b
C
C
探索新知
2
知识点
求整式的值
例6
探索新知
先将式子化简,
再代入数值进行
计算比较简便.
探索新知
总 结
求整式的值时,一般是先化简(去括号、合并同类项),再把字母的值代入化简后的式子求值.
典题精讲
3.已知a2+2a=1,则整式2a2+4a-1的值是( )
A.0 B.1 C.-1 D.-2
2.已知3a-2b=2,则9a-6b=_______.
1.若多项式3x3-2x2+3x+1与多项式x2-2mx3+2x+3的
和为二次三项式,则m=________.
6
B
学以致用
小试牛刀
1.一般地,几个整式相加减,如果有括号就先__________,然
后再______________.整式加减的最后结果中不能含有同类
项,即要合并到不能再合并为止.
去括号
合并同类项
2.已知x2+2x-1=0,则3x2+6x-2=________.
1
小试牛刀
3.多项式3a2-6a+4与4a2+5a-3的差是( )
A.-a2-11a+7 B.-a2-a+1
C.a2+11a-7 D.a2-a+1
A
4.若A=x2-2xy+y2,B=x2+2xy+y2,则4xy=( )
A.A+B B.B-A
C.A-B D.2A-2B
B
小试牛刀
5.多项式(xyz2+4xy-1)+(-3xy+2z2yx-3)-(3xyz2+
xy)的值( )
A.与x,y,z的大小无关
B.与x,y的大小有关,而与z的大小无关
C.与x的大小有关,而与y,z的大小无关
D.与x,y,z的大小都有关
A
小试牛刀
6.若(A+1)2+|b-2|=0,则化简A(x2y+xy2)-b(x2y-xy2)的
结果为( )
A.3x2y B.-3x2y+xy2
C.-3x2y+3xy2 D.3x2y-xy2
B
7.若A-b=2,b-c=-3,则A-c等于( )
A.1 B.-1
C.5 D.-5
A
小试牛刀
8.先化简,再求值:2(A2b+2b3-Ab3)+3A3-(2bA2-3Ab2
+3A3)-4b3,其中A=-3,b=2.
解:原式=2a2b+4b3-2ab3+3a3-2a2b+3ab2-3a3-4b3=-2ab3+3ab2.
当a=-3,b=2时,
原式=-2×(-3)×23+3×(-3)×22=48-36=12.
小试牛刀
9.已知A+b=7,Ab=10,求(5Ab+4A+7b)+(6A-
3Ab)-(4Ab-3b)的值.
解:原式=5ab+4a+7b+6a-3ab-4ab+3b
=10(a+b)-2ab.
当a+b=7,ab=10时,
原式=10×7-2×10=50.
小试牛刀
10.当式子(2x+4)2+5取得最小值时,求式子5x-[-2x2-
(-5x+2)]的值.
解:因为当(2x+4)2+5取得最小值时,(2x+4)2=0,
所以2x+4=0,解得x=-2.
原式=5x-(-2x2+5x-2)=5x+2x2-5x+2=2x2+2.
当x=-2时,原式=2×(-2)2+2=10.
课堂小结
课堂小结
整式加减的一般步骤是:先去括号,再合并同类项.
注意:
(1)整式加减运算的过程中,一般把多项式用括号括起来;
(2)整式加减的最后结果中不能含有同类项,即要合并到不
能再合并为止.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
