人教版(新)七上-3.1.2 等式的性质【优质课件】
文档属性
| 名称 | 人教版(新)七上-3.1.2 等式的性质【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
3.1.2 等式的性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习提问 引出问题。
(1)什么叫做方程?
(2)什么叫做一元一次方程?
(3)一元一次方程有哪几个特征?
①只含有一个未知数;
②未知数的次数都是1;
③整式方程.
(4)请你举出一个一元一次方程的例子.
新课精讲
探索新知
1
知识点
等式的性质1
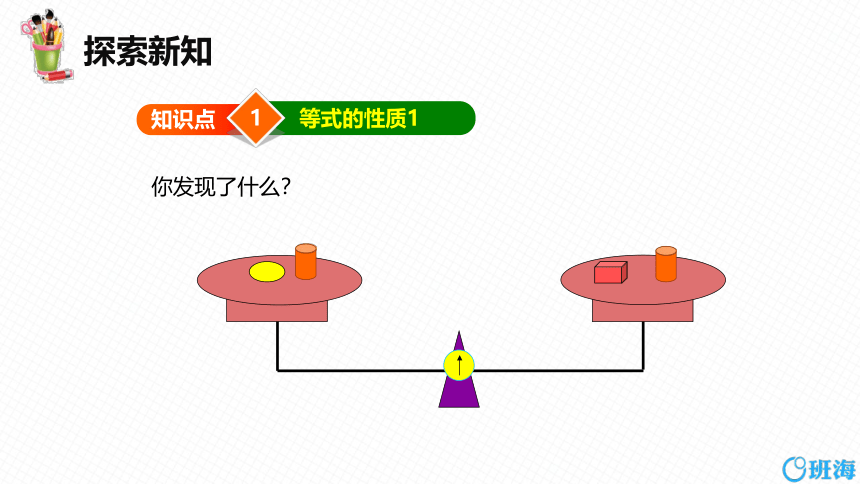
你发现了什么?
探索新知
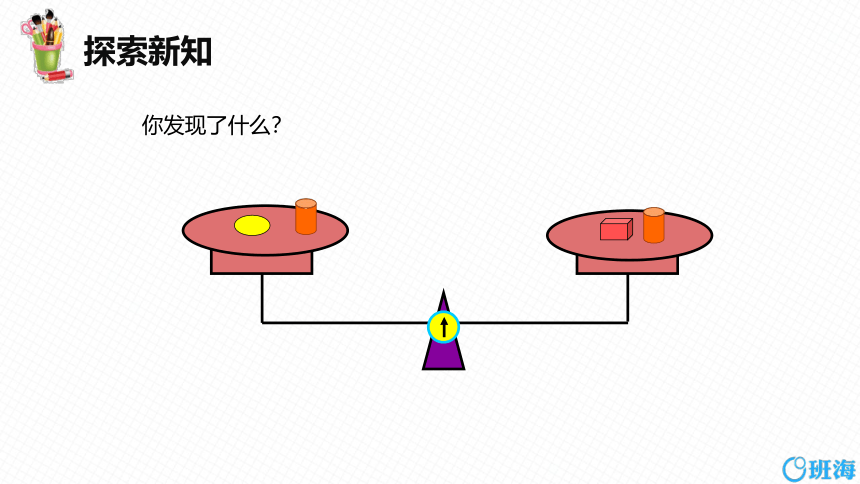
你发现了什么?
探索新知
归 纳
我们可以发现,如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡.
探索新知
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等,用公式表示:如果a=b,那么a±c=b±c;这里的a,b,c可以是具体的一个数,也可以是一个代数式.
探索新知
例1 根据等式的性质填空,并在后面的括号内填上变形的根据.
(1)如果4x=x-2,那么4x-____=-2( );
(2)如果2x+9=1,那么2x=1-____( );
x
9
等式的性质1
等式的性质1
导引:(1)中方程的右边由x-2到-2,减了x,所以左边也要减x;(2)中方程的左边由2x+9到2x,减了9,所以右边也要减9.
典题精讲
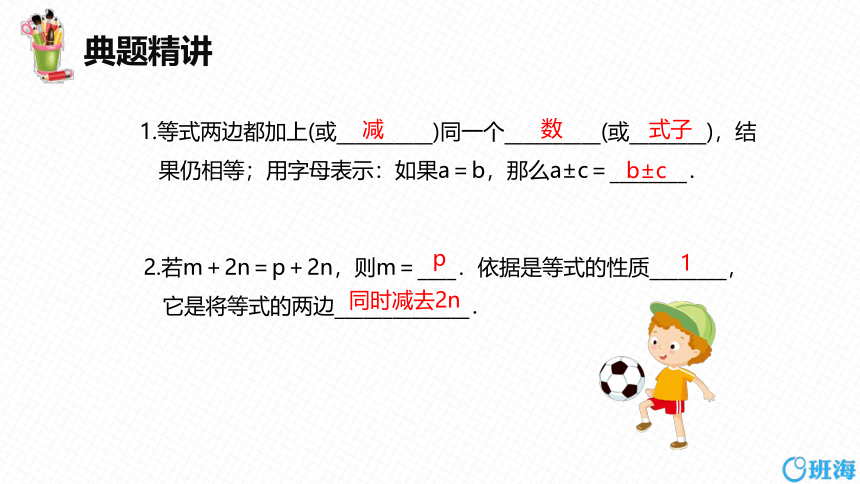
1.等式两边都加上(或__________)同一个__________(或________),结
果仍相等;用字母表示:如果a=b,那么a±c=________.
2.若m+2n=p+2n,则m=____.依据是等式的性质________,
它是将等式的两边______________.
减
数
式子
b±c
p
1
同时减去2n
典题精讲
3.下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
C
探索新知
2
知识点
等式的性质2
×3
÷ 3
如:2=2 那么2× 3=2×3
如:6=6 那么6÷2=6÷2
探索新知
等式的性质2:等式两边乘同一个数,或除以同一个不为0的
数,结果仍相等,用公式表示:如果a=b,那么ac=bc,
(c≠0).等式的性质2中,除以的同一个数不能为0.
探索新知
例2 根据等式的性质填空,并在后面的括号内填 上变形的根据.
(1)如果- = ,那么x=____( );
(2)如果0.4a=3b,那么a=____( ).
等式的性质2
等式的性质2
导引: (1)中方程的左边由- 到x,乘了-3,所以右边也要乘-3;(2)中方程的左边由0.4a到a除以了0.4,所以右边也要除以0.4,即乘 .
典题精讲
1.等式2x-y=10变形为-4x+2y=-20的依据为( )
A.等式基本性质1 B.等式基本性质2
C.分数的基本性质 D.乘法分配律
B
2.已知x=y,下列各式:3x=3y,-2x=-2y, =1,
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
C
典题精讲
3.下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 -1=x,那么2x+1-1=3x
B
探索新知
3
知识点
利用等式的性质变形
例3 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
分析:要使方程x+7 = 26转化为x=a (常数)的形式,需去掉方程左边 的7,利用等式的性质1,方程两边减7就得出x的值.你可以类似地考虑另两 个方程如何转化为x=a的形式.
探索新知
解:(1)两边减7,得x+7-7=26-7.
于是x=19.
(2)两边除以-5,得
于是x= - 4.
(3)两边加5,得
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
探索新知
例4 若x=1是关于x的方程ax+b=c的解,求:
(1)(a+b-c)2的值;
(2) 的值;
(3)|c-a-b-1|的值.
解:因为x=1是关于x的方程ax+b=c的解,
所以a+b=c. (a+b-c)2=[(a+b)-c]2=(c-c)2=0.
解:
解:c-a-b-1|=|c-(a+b)-1|=|c-c-1|=1.
探索新知
总 结
本例中a,b,c的值无法求出,表面上看似无法求出相关式子的值,而运用整体思想就能达到求解的目的.
探索新知
例5 已知2x2+3x=5,求多项式-4x2-6x+6的值.
导引:要求多项式-4x2-6x+6的值,求出x的值或-4x2-6x
的值即可.而x的值目前我们无法求出,所以我们需求出
-4x2-6x的值.
解:因为2x2+3x=5,
所以-4x2-6x=-10(等式两边同时乘-2),
所以-4x2-6x+6=-4(等式两边同时加6).
探索新知
总 结
利用等式的性质可以将等式作很多变形,求某个多项式的值时,可以巧借等式的性质将已知的条件进行变形,使之与要求的多项式相同.
典题精讲
1.在横线上填上适当的数或式子:
(1)如果a+3=b-1,那么a+4=________;
(2)如果 x=3,那么x=________.
2.利用等式的性质解下列方程并检验:
(1)x-5=6; (2)5x+4=0.
b
12
X=11
检验略。
学以致用
小试牛刀
1.小李在解方程5a-x=13(x为未知数)时,误将-x看作+x,解得方程
的解x=-2,则原方程的解为 .
x=2
2.将等式5a-3b=4a-3b变形,过程如下:
因为5a-3b=4a-3b,
5a=4a(第一步),
5=4(第二步).
上述过程中,第一步的依据是 ,第二步得出错误的结论,其原因 .
等式的性质1
等式的两边同除以了一个可能等于0的数a
小试牛刀
3.(1)如果-3(x+3)=6,那么x+3= ,根据
是 .
(2)如果3a+7b=4b-3,那么a+b= ,变形根据
是 .
-2
等式的性质2
-1
等式的性质1和等式的性质2
2
4.当x= 时,式子 的值是1.
小试牛刀
5.下列等式的变形正确的是( )
A.若 =2x,则3x-2=4x B.若 =2x,则3x-1=2x
C.若 =2x,则5x-1=0 D.若 =2x,则3x-1=4x
D
6.如果不为0的四条线段的长度分别为a,b,c,d,且满足ab=cd,
那么( )
A. B.
C. D.
C
小试牛刀
7.如果式子5x-4的值与- 互为倒数,那么x的值是( )
A. B. C. D.
D
8.如图所示,天平上放有苹果、香蕉、砝码,且两个天平都平衡,
则一个苹果的质量是一个香蕉的质量的( )
A.
B.
C. 2倍
D. 3倍
B
小试牛刀
9.已知等式(a-2)x2+ax+1=0是关于x的一元一次方程,求这个方程的解.
解:因为(a-2)x2+ax+1=0是关于x的一元一次方程,
所以a-2=0,即a=2.所以原方程变为2x+1=0,
根据等式的性质,得x=
小试牛刀
10.某旅客携带了30 kg的行李从南京禄口国际机场乘飞机去天津.按
民航的规定,旅客最多可免费携带20 kg的行李,超重部分每千
克按飞机票价格的1.5%购买行李票,现该旅客购买了120元的
行李票,求他的飞机票价格是多少元
解:设他的飞机票价格是x元.由题意,得
(30-20)×1.5%x=120,即0.15x=120.
根据等式的性质,得x=800.
答:他的飞机票价格是800元.
11.能否找到一个x值,使式子4x+5与6x+9的值相等 若能,请找
出x的值;若不能,请说明理由.
解:若存在使4x+5=6x+9的x的值,
则可根据等式的性质,两边都减去6x,得
4x+5-6x=6x+9-6x,即-2x+5=9,
两边都减去5,得-2x=4, 两边都除以-2,得x=-2.
所以当x=-2时,4x+5与6x+9的值相等.
小试牛刀
课堂小结
课堂小结
等式的性质:
1. 等式两边加(或减) 同一个数(或式子),结果仍相等.
如果 a=b 那么a ± c=b ± c
2. 等式两边乘同一个数或除以同一个不为0的 数,结果仍相等.
如果 a=b 那么 ac = bc如果 a=b 那么
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.1.2 等式的性质
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
复习提问 引出问题。
(1)什么叫做方程?
(2)什么叫做一元一次方程?
(3)一元一次方程有哪几个特征?
①只含有一个未知数;
②未知数的次数都是1;
③整式方程.
(4)请你举出一个一元一次方程的例子.
新课精讲
探索新知
1
知识点
等式的性质1
你发现了什么?
探索新知
你发现了什么?
探索新知
归 纳
我们可以发现,如果在平衡的天平的两边都加(或减)同样的量,天平还保持平衡.
探索新知
等式的性质1:
等式两边加(或减)同一个数(或式子),结果仍相等,用公式表示:如果a=b,那么a±c=b±c;这里的a,b,c可以是具体的一个数,也可以是一个代数式.
探索新知
例1 根据等式的性质填空,并在后面的括号内填上变形的根据.
(1)如果4x=x-2,那么4x-____=-2( );
(2)如果2x+9=1,那么2x=1-____( );
x
9
等式的性质1
等式的性质1
导引:(1)中方程的右边由x-2到-2,减了x,所以左边也要减x;(2)中方程的左边由2x+9到2x,减了9,所以右边也要减9.
典题精讲
1.等式两边都加上(或__________)同一个__________(或________),结
果仍相等;用字母表示:如果a=b,那么a±c=________.
2.若m+2n=p+2n,则m=____.依据是等式的性质________,
它是将等式的两边______________.
减
数
式子
b±c
p
1
同时减去2n
典题精讲
3.下列各种变形中,不正确的是( )
A.由2+x=5可得到x=5-2
B.由3x=2x-1可得到3x-2x=-1
C.由5x=4x+1可得到4x-5x=1
D.由6x-2x=-3可得到6x=2x-3
C
探索新知
2
知识点
等式的性质2
×3
÷ 3
如:2=2 那么2× 3=2×3
如:6=6 那么6÷2=6÷2
探索新知
等式的性质2:等式两边乘同一个数,或除以同一个不为0的
数,结果仍相等,用公式表示:如果a=b,那么ac=bc,
(c≠0).等式的性质2中,除以的同一个数不能为0.
探索新知
例2 根据等式的性质填空,并在后面的括号内填 上变形的根据.
(1)如果- = ,那么x=____( );
(2)如果0.4a=3b,那么a=____( ).
等式的性质2
等式的性质2
导引: (1)中方程的左边由- 到x,乘了-3,所以右边也要乘-3;(2)中方程的左边由0.4a到a除以了0.4,所以右边也要除以0.4,即乘 .
典题精讲
1.等式2x-y=10变形为-4x+2y=-20的依据为( )
A.等式基本性质1 B.等式基本性质2
C.分数的基本性质 D.乘法分配律
B
2.已知x=y,下列各式:3x=3y,-2x=-2y, =1,
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
C
典题精讲
3.下列变形,正确的是( )
A.如果a=b,那么
B.如果 ,那么a=b
C.如果a2=3a,那么a=3
D.如果 -1=x,那么2x+1-1=3x
B
探索新知
3
知识点
利用等式的性质变形
例3 利用等式的性质解下列方程:
(1) x+7 = 26; (2) -5x=20; (3) -5=4.
分析:要使方程x+7 = 26转化为x=a (常数)的形式,需去掉方程左边 的7,利用等式的性质1,方程两边减7就得出x的值.你可以类似地考虑另两 个方程如何转化为x=a的形式.
探索新知
解:(1)两边减7,得x+7-7=26-7.
于是x=19.
(2)两边除以-5,得
于是x= - 4.
(3)两边加5,得
解以x为未知数的方程,就是把方程逐步转化为x= a (常 数)的形式,等式的性质是转化的重要依据.
探索新知
例4 若x=1是关于x的方程ax+b=c的解,求:
(1)(a+b-c)2的值;
(2) 的值;
(3)|c-a-b-1|的值.
解:因为x=1是关于x的方程ax+b=c的解,
所以a+b=c. (a+b-c)2=[(a+b)-c]2=(c-c)2=0.
解:
解:c-a-b-1|=|c-(a+b)-1|=|c-c-1|=1.
探索新知
总 结
本例中a,b,c的值无法求出,表面上看似无法求出相关式子的值,而运用整体思想就能达到求解的目的.
探索新知
例5 已知2x2+3x=5,求多项式-4x2-6x+6的值.
导引:要求多项式-4x2-6x+6的值,求出x的值或-4x2-6x
的值即可.而x的值目前我们无法求出,所以我们需求出
-4x2-6x的值.
解:因为2x2+3x=5,
所以-4x2-6x=-10(等式两边同时乘-2),
所以-4x2-6x+6=-4(等式两边同时加6).
探索新知
总 结
利用等式的性质可以将等式作很多变形,求某个多项式的值时,可以巧借等式的性质将已知的条件进行变形,使之与要求的多项式相同.
典题精讲
1.在横线上填上适当的数或式子:
(1)如果a+3=b-1,那么a+4=________;
(2)如果 x=3,那么x=________.
2.利用等式的性质解下列方程并检验:
(1)x-5=6; (2)5x+4=0.
b
12
X=11
检验略。
学以致用
小试牛刀
1.小李在解方程5a-x=13(x为未知数)时,误将-x看作+x,解得方程
的解x=-2,则原方程的解为 .
x=2
2.将等式5a-3b=4a-3b变形,过程如下:
因为5a-3b=4a-3b,
5a=4a(第一步),
5=4(第二步).
上述过程中,第一步的依据是 ,第二步得出错误的结论,其原因 .
等式的性质1
等式的两边同除以了一个可能等于0的数a
小试牛刀
3.(1)如果-3(x+3)=6,那么x+3= ,根据
是 .
(2)如果3a+7b=4b-3,那么a+b= ,变形根据
是 .
-2
等式的性质2
-1
等式的性质1和等式的性质2
2
4.当x= 时,式子 的值是1.
小试牛刀
5.下列等式的变形正确的是( )
A.若 =2x,则3x-2=4x B.若 =2x,则3x-1=2x
C.若 =2x,则5x-1=0 D.若 =2x,则3x-1=4x
D
6.如果不为0的四条线段的长度分别为a,b,c,d,且满足ab=cd,
那么( )
A. B.
C. D.
C
小试牛刀
7.如果式子5x-4的值与- 互为倒数,那么x的值是( )
A. B. C. D.
D
8.如图所示,天平上放有苹果、香蕉、砝码,且两个天平都平衡,
则一个苹果的质量是一个香蕉的质量的( )
A.
B.
C. 2倍
D. 3倍
B
小试牛刀
9.已知等式(a-2)x2+ax+1=0是关于x的一元一次方程,求这个方程的解.
解:因为(a-2)x2+ax+1=0是关于x的一元一次方程,
所以a-2=0,即a=2.所以原方程变为2x+1=0,
根据等式的性质,得x=
小试牛刀
10.某旅客携带了30 kg的行李从南京禄口国际机场乘飞机去天津.按
民航的规定,旅客最多可免费携带20 kg的行李,超重部分每千
克按飞机票价格的1.5%购买行李票,现该旅客购买了120元的
行李票,求他的飞机票价格是多少元
解:设他的飞机票价格是x元.由题意,得
(30-20)×1.5%x=120,即0.15x=120.
根据等式的性质,得x=800.
答:他的飞机票价格是800元.
11.能否找到一个x值,使式子4x+5与6x+9的值相等 若能,请找
出x的值;若不能,请说明理由.
解:若存在使4x+5=6x+9的x的值,
则可根据等式的性质,两边都减去6x,得
4x+5-6x=6x+9-6x,即-2x+5=9,
两边都减去5,得-2x=4, 两边都除以-2,得x=-2.
所以当x=-2时,4x+5与6x+9的值相等.
小试牛刀
课堂小结
课堂小结
等式的性质:
1. 等式两边加(或减) 同一个数(或式子),结果仍相等.
如果 a=b 那么a ± c=b ± c
2. 等式两边乘同一个数或除以同一个不为0的 数,结果仍相等.
如果 a=b 那么 ac = bc如果 a=b 那么
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
