人教版(新)七上-3.2 解一元一次方程(一)——合并同类项与移项 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-3.2 解一元一次方程(一)——合并同类项与移项 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:27:48 | ||
图片预览











文档简介
(共36张PPT)
3.2 解一元一次方程(一)——合并同类项与移项
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
等式两边都加上(或减去)同一个代数式,所得结果仍是等式.
等式的基本性质2:
等式两边都乘以(或除以)同一个不等于0的数,所得结果仍是等式.
等式的基本性质1:
新课精讲
探索新知
1
知识点
移 项
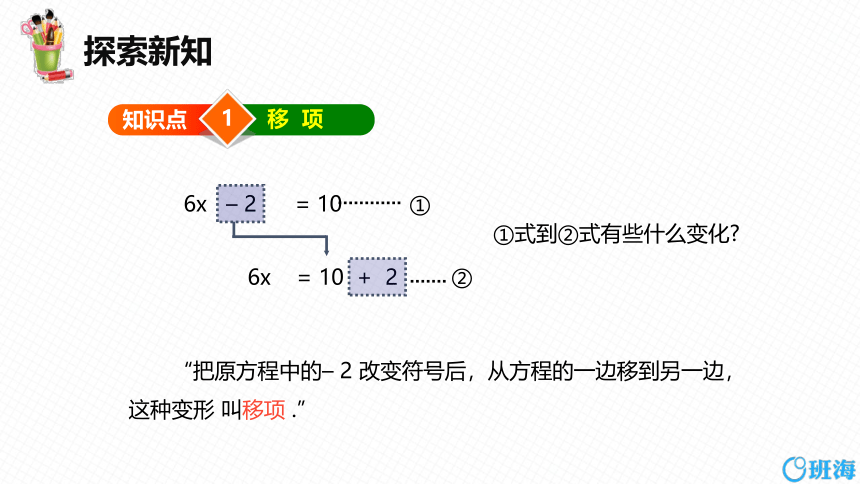
6x – 2 = 10
6x = 10 + 2
①
②
①式到②式有些什么变化
“把原方程中的– 2 改变符号后,从方程的一边移到另一边,这种变形 叫移项 .”
探索新知
1.定义:把等式一边的某项变号后移到另一边做移项.
2.方法:把方程右边含有未知数的项改变符号后移到方程左边,把方
程左边不含未知数的项改变符号后移到方程右边,即“常数
右边凑热闹,未知左边来报到”.
探索新知
例1 将方程5x+1=2x-3移项后,可得( )
A.5x-2x=-3+1
B.5x-2x=-3-1
C.5x+2x=-3-1
D.5x+2x=1-3
导引:A.常数项1移项时没有变号;C.2x移项时没有变号;D.2x和常数
项1移项时均未变号,故选B.
B
探索新知
总 结
移项与交换律的根本区别是移项时移动的项要跨越等号,并且一定要记住移项要变号.
典题精讲
1.把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做________,依
据是__________________________.
2.解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
移项
等式的性质1
C
典题精讲
3.解下列方程时,既要移含未知数的项,又要移常数项的是( )
A.2x=6-3x B.2x-4=3x+1
C.2x-2-x=1 D.x-5=7
B
4.下列各式中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
D
探索新知
2
知识点
用移项法解一元一次方程
下面的框图表示了解这个方程的流程.
3x+20=4x-25
3x -4x= -25-20
- x= -45
x=45
移项
系数化为1
合并同类项
由上可知,这个班有45名学生.
探索新知
归 纳
移项解一元一次方程一般步骤:
①移项
②合并同类项
③系数化为1
探索新知
例2 解下列方程:
解: 移项,得3x+2x=32 -7.
合并同类项,得5x=25.
系数化为1,得x=5.
解: 移项,得
合并同类项,得
系数化为1,得x= - 8.
探索新知
总 结
移项法是解简易方程的最基本的方法,其目的是便于合并同类项,要把移项与多项式项的移动区别开来;解题的关键是要记住“移项要变号”这一要诀;其步骤为“一移二并三化”.
典题精讲
1.解下列方程:
2.方程3x-4=3-2x的解答过程的正确顺序是( )
①合并同类项,得5x=7; ②移项,得3x+2x=3+4;
③系数化为1,得x= .
A.①②③ B.③②① C.②①③ D.③①②
x=1
C
x=24
典题精讲
3.关于x的方程4x-6=3m与x-1=2有相同的解,则m等于( )
A.-2
B.2
C.-3
D.3
B
探索新知
例3 某制药厂制造一批药品,如用旧工艺,则排量要比环保限制
的最大量还多200 t;如用新工艺,则废水排量比环保限制的
最大量少100 t新、旧工艺的废水排量之比为2: 5,两种工艺
的废水排量各是多少?
分析:因为新、旧工艺的废水排量之比为2: 5,所以可设它们分别为
2xt和5xt,再根据它们与环保限制的最大量之间的关系列方程.
探索新知
解:设新、旧工艺的废水排量分别为2xt 和5xt .
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100.
移项,得5x-2x=100+200.
合并同类项,得3x=300 .
系数化为1,得x= 100.
所以2x=200,5x=500.
答:新、旧工艺产生的废水排量分别为200 t和500 t.
等号两边代表哪个数量?
探索新知
总 结
解决比例问题,一般设每份为未知数,用含
未知数的式子表示相关的量,再根据等量关系列出
方程.
探索新知
例4 已知|3x-6|+(2y-8)2=0,求2x-y的值.
解: 由题意,得|3x-6|=0,(2y-8)2=0.
所以3x-6=0,2y-8=0.
解得x=2,y=4.
所以2x-y=2×2-4=0.
探索新知
例5 单项式7x2m-1yn+2与-9x3y-n+4的和仍是单项式,求m-n的值.
解:由题意,得2m-1=3,n+2=-n+4,
解得m=2,n=1.
则m-n=2-1=1.
典题精讲
1.王芳和李丽同时采摘樱桃,王芳平均每小时采摘8 kg,李丽平均每小时采摘 7 kg.采摘结束后王芳从她采摘的樱桃中取出0.25 kg给了李丽,这时两人的 樱桃一样多.她们采摘用了多少时间?
解:设采摘了x h.
8x-0.25=7x+0.25,
x =0.5.
典题精讲
2.若-2x2m+1y6与 x3m-1y10+4n是同类项,则m,n的值分别为( )
A.2,-1 B.-2,1 C.-1,2 D.-2,-1
A
3.若“☆”是新规定的某种运算符号,x☆y=xy+x+y,则2☆m=-16
中,m的值为( )
A.8 B.-8 C.6 D.-6
4.某商品的标价为200元,8折销售仍赚40元,则该商品的进价为( )元.
A.140 B.120 C.160 D.100
D
B
学以致用
小试牛刀
1.移项:方程中的任何一项,都可以在______________后,从方程的一边
移到另一边,这类变形叫做移项.这个法则叫做移项法则,移项的根
据是__________________.
2.解较简单的一元一次方程的步骤:
(1)移项.将常数项放在_____________,未知项放在_____________;
(2)合并.将同类项进行_____________,一般要逆用_____________;
(3)系数化为1.利用等式的性质________,化成x=a(a是常数)的形式.
改变符号
等式的性质1
方程的右边
方程的左边
合并
分配律
2
小试牛刀
3.(1)若3x+5=2,则3x=________;
(2)若x-6=2009-y,则x+y=________.
4.若单项式3a b与 是同类项,则x的值为________.
5.若x=-2是方程mx-6=15+m的解,则m的值为________.
6.已知关于x的方程3x-7=2x+a的解与方程4x+2=7-x的解相同,则
a的值为________.
7.某地甲、乙两站间的距离为365km,一列慢车从甲站开往乙站,每小时
行驶65km,慢车行驶1h后,另有一列快车从乙站开往甲站,每小时行
驶85km,快车行驶________h后与慢车相遇.
-3
3x+1
2015
3
-7
-6
2
小试牛刀
8.下列变形中,属于移项的是( )
A.由3x=-1,得 B .由 ,得x=4
C.由3x+5=0,得3x=-5 D.由-3x+3=0,得3-3x=0
C
9.方程4x-2=3-x有下列解答过程:①合并同类项,得5x=5;②移项,
得4x+x=3+2;③系数化为1,得x=1.正确的解题顺序是( )
A.①②③ B .③②①
C.②①③ D.③①②
C
小试牛刀
10.在某地区2014年“地球停电一小时”活动的烛光晚餐中,设有x排座
位,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则
下列方程正确的是( )
A.30x-8=31x+26
B.30x+8=31x+26
C.30x-8=31x-26
D.30x+8=31x-26
D
小试牛刀
11.解下列方程:
(1) (2)61-2x=64+x
(3)12t+6=-3t -7 (4)
(5)9x+8-7x=3x (6)
(7)2x-5+4x=5x-3 (8)
x=2
x=-1
n=24
x=8
x=2
小试牛刀
12.当x取何值时,2x+3与-5x+6满足下列条件:
(1)相等;
(2)互为相反数;
(3)2x+3比-5x+6小10?
x=3
x=-1
小试牛刀
13.把一些图书分给某班学生阅读,如果每人分3本,那么剩余20本;如果
每人分4本,那么还缺25本.请根据以上信息,提出一个用一元一次方
程解决的问题,并写出解答过程.
答案不唯一.如这个班有多少名学生?
设这个班有x名学生.
根据题意,列方程得3x+20=4x-25
解得x=45
小试牛刀
14.某人承包了一项零件加工任务,限期完成,若他每天生产13个,则到期
时还差20个零件;若他每天生产16个,则到期时还能多做16个零件.
生产期限是多少天?承包加工的零件有多少个?
设生产期限是x天.
根据题意,列方程得13x+20=16x-16,
解得x=12.
所以生产期限是12天,承包加工的零件有13×12+20=176(个)
课堂小结
课堂小结
用移项法解一元一次方程的一般步骤:
移项→合并同类项→系数化为1.
移项的原则:
未知项左边来报到,常数项右边凑热闹.
移项的方法:
把方程中的某些项改变符号后,从方程的一边移到另一边,即移项要变号.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.2 解一元一次方程(一)——合并同类项与移项
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
等式两边都加上(或减去)同一个代数式,所得结果仍是等式.
等式的基本性质2:
等式两边都乘以(或除以)同一个不等于0的数,所得结果仍是等式.
等式的基本性质1:
新课精讲
探索新知
1
知识点
移 项
6x – 2 = 10
6x = 10 + 2
①
②
①式到②式有些什么变化
“把原方程中的– 2 改变符号后,从方程的一边移到另一边,这种变形 叫移项 .”
探索新知
1.定义:把等式一边的某项变号后移到另一边做移项.
2.方法:把方程右边含有未知数的项改变符号后移到方程左边,把方
程左边不含未知数的项改变符号后移到方程右边,即“常数
右边凑热闹,未知左边来报到”.
探索新知
例1 将方程5x+1=2x-3移项后,可得( )
A.5x-2x=-3+1
B.5x-2x=-3-1
C.5x+2x=-3-1
D.5x+2x=1-3
导引:A.常数项1移项时没有变号;C.2x移项时没有变号;D.2x和常数
项1移项时均未变号,故选B.
B
探索新知
总 结
移项与交换律的根本区别是移项时移动的项要跨越等号,并且一定要记住移项要变号.
典题精讲
1.把方程3y-6=y+8变形为3y-y=8+6,这种变形叫做________,依
据是__________________________.
2.解方程时,移项法则的依据是( )
A.加法交换律 B.加法结合律
C.等式的性质1 D.等式的性质2
移项
等式的性质1
C
典题精讲
3.解下列方程时,既要移含未知数的项,又要移常数项的是( )
A.2x=6-3x B.2x-4=3x+1
C.2x-2-x=1 D.x-5=7
B
4.下列各式中的变形,属于移项的是( )
A.由3x-2y-1得-1-2y+3x
B.由9x-3=x+5得9x-3=5+x
C.由4-x=5x-2得5x-2=4-x
D.由2-x=x-2得2+2=x+x
D
探索新知
2
知识点
用移项法解一元一次方程
下面的框图表示了解这个方程的流程.
3x+20=4x-25
3x -4x= -25-20
- x= -45
x=45
移项
系数化为1
合并同类项
由上可知,这个班有45名学生.
探索新知
归 纳
移项解一元一次方程一般步骤:
①移项
②合并同类项
③系数化为1
探索新知
例2 解下列方程:
解: 移项,得3x+2x=32 -7.
合并同类项,得5x=25.
系数化为1,得x=5.
解: 移项,得
合并同类项,得
系数化为1,得x= - 8.
探索新知
总 结
移项法是解简易方程的最基本的方法,其目的是便于合并同类项,要把移项与多项式项的移动区别开来;解题的关键是要记住“移项要变号”这一要诀;其步骤为“一移二并三化”.
典题精讲
1.解下列方程:
2.方程3x-4=3-2x的解答过程的正确顺序是( )
①合并同类项,得5x=7; ②移项,得3x+2x=3+4;
③系数化为1,得x= .
A.①②③ B.③②① C.②①③ D.③①②
x=1
C
x=24
典题精讲
3.关于x的方程4x-6=3m与x-1=2有相同的解,则m等于( )
A.-2
B.2
C.-3
D.3
B
探索新知
例3 某制药厂制造一批药品,如用旧工艺,则排量要比环保限制
的最大量还多200 t;如用新工艺,则废水排量比环保限制的
最大量少100 t新、旧工艺的废水排量之比为2: 5,两种工艺
的废水排量各是多少?
分析:因为新、旧工艺的废水排量之比为2: 5,所以可设它们分别为
2xt和5xt,再根据它们与环保限制的最大量之间的关系列方程.
探索新知
解:设新、旧工艺的废水排量分别为2xt 和5xt .
根据废水排量与环保限制最大量之间的关系,得
5x-200=2x+100.
移项,得5x-2x=100+200.
合并同类项,得3x=300 .
系数化为1,得x= 100.
所以2x=200,5x=500.
答:新、旧工艺产生的废水排量分别为200 t和500 t.
等号两边代表哪个数量?
探索新知
总 结
解决比例问题,一般设每份为未知数,用含
未知数的式子表示相关的量,再根据等量关系列出
方程.
探索新知
例4 已知|3x-6|+(2y-8)2=0,求2x-y的值.
解: 由题意,得|3x-6|=0,(2y-8)2=0.
所以3x-6=0,2y-8=0.
解得x=2,y=4.
所以2x-y=2×2-4=0.
探索新知
例5 单项式7x2m-1yn+2与-9x3y-n+4的和仍是单项式,求m-n的值.
解:由题意,得2m-1=3,n+2=-n+4,
解得m=2,n=1.
则m-n=2-1=1.
典题精讲
1.王芳和李丽同时采摘樱桃,王芳平均每小时采摘8 kg,李丽平均每小时采摘 7 kg.采摘结束后王芳从她采摘的樱桃中取出0.25 kg给了李丽,这时两人的 樱桃一样多.她们采摘用了多少时间?
解:设采摘了x h.
8x-0.25=7x+0.25,
x =0.5.
典题精讲
2.若-2x2m+1y6与 x3m-1y10+4n是同类项,则m,n的值分别为( )
A.2,-1 B.-2,1 C.-1,2 D.-2,-1
A
3.若“☆”是新规定的某种运算符号,x☆y=xy+x+y,则2☆m=-16
中,m的值为( )
A.8 B.-8 C.6 D.-6
4.某商品的标价为200元,8折销售仍赚40元,则该商品的进价为( )元.
A.140 B.120 C.160 D.100
D
B
学以致用
小试牛刀
1.移项:方程中的任何一项,都可以在______________后,从方程的一边
移到另一边,这类变形叫做移项.这个法则叫做移项法则,移项的根
据是__________________.
2.解较简单的一元一次方程的步骤:
(1)移项.将常数项放在_____________,未知项放在_____________;
(2)合并.将同类项进行_____________,一般要逆用_____________;
(3)系数化为1.利用等式的性质________,化成x=a(a是常数)的形式.
改变符号
等式的性质1
方程的右边
方程的左边
合并
分配律
2
小试牛刀
3.(1)若3x+5=2,则3x=________;
(2)若x-6=2009-y,则x+y=________.
4.若单项式3a b与 是同类项,则x的值为________.
5.若x=-2是方程mx-6=15+m的解,则m的值为________.
6.已知关于x的方程3x-7=2x+a的解与方程4x+2=7-x的解相同,则
a的值为________.
7.某地甲、乙两站间的距离为365km,一列慢车从甲站开往乙站,每小时
行驶65km,慢车行驶1h后,另有一列快车从乙站开往甲站,每小时行
驶85km,快车行驶________h后与慢车相遇.
-3
3x+1
2015
3
-7
-6
2
小试牛刀
8.下列变形中,属于移项的是( )
A.由3x=-1,得 B .由 ,得x=4
C.由3x+5=0,得3x=-5 D.由-3x+3=0,得3-3x=0
C
9.方程4x-2=3-x有下列解答过程:①合并同类项,得5x=5;②移项,
得4x+x=3+2;③系数化为1,得x=1.正确的解题顺序是( )
A.①②③ B .③②①
C.②①③ D.③①②
C
小试牛刀
10.在某地区2014年“地球停电一小时”活动的烛光晚餐中,设有x排座
位,每排坐30人,则有8人无座位;每排坐31人,则空26个座位,则
下列方程正确的是( )
A.30x-8=31x+26
B.30x+8=31x+26
C.30x-8=31x-26
D.30x+8=31x-26
D
小试牛刀
11.解下列方程:
(1) (2)61-2x=64+x
(3)12t+6=-3t -7 (4)
(5)9x+8-7x=3x (6)
(7)2x-5+4x=5x-3 (8)
x=2
x=-1
n=24
x=8
x=2
小试牛刀
12.当x取何值时,2x+3与-5x+6满足下列条件:
(1)相等;
(2)互为相反数;
(3)2x+3比-5x+6小10?
x=3
x=-1
小试牛刀
13.把一些图书分给某班学生阅读,如果每人分3本,那么剩余20本;如果
每人分4本,那么还缺25本.请根据以上信息,提出一个用一元一次方
程解决的问题,并写出解答过程.
答案不唯一.如这个班有多少名学生?
设这个班有x名学生.
根据题意,列方程得3x+20=4x-25
解得x=45
小试牛刀
14.某人承包了一项零件加工任务,限期完成,若他每天生产13个,则到期
时还差20个零件;若他每天生产16个,则到期时还能多做16个零件.
生产期限是多少天?承包加工的零件有多少个?
设生产期限是x天.
根据题意,列方程得13x+20=16x-16,
解得x=12.
所以生产期限是12天,承包加工的零件有13×12+20=176(个)
课堂小结
课堂小结
用移项法解一元一次方程的一般步骤:
移项→合并同类项→系数化为1.
移项的原则:
未知项左边来报到,常数项右边凑热闹.
移项的方法:
把方程中的某些项改变符号后,从方程的一边移到另一边,即移项要变号.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
