人教版(新)七上-3.3 解一元一次方程(二)——去括号与去分母 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-3.3 解一元一次方程(二)——去括号与去分母 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览









文档简介
(共41张PPT)
3.3 解一元一次方程(二)
—去括号与去分母
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
解方程:
新课精讲
探索新知
1
知识点
一般行程问题
1. 行程问题中的基本关系式:
路程=速度×时间,
时间=路程÷速度,
速度=路程÷时间.
探索新知
2. 行程问题中的相等关系:
(1)相遇问题中的相等关系:
①若甲、乙相向而行,甲走的路程+乙走的路程=甲、乙出发点之
间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
(2)追及问题中的相等关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间.
探索新知
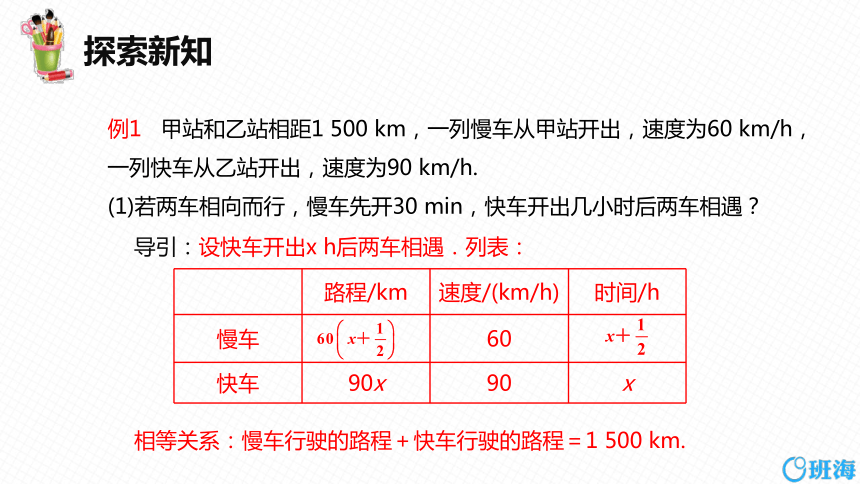
例1 甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
导引:设快车开出x h后两车相遇.列表:
相等关系:慢车行驶的路程+快车行驶的路程=1 500 km.
路程/km 速度/(km/h) 时间/h
慢车 60
快车 90x 90 x
探索新知
解:设快车开出x h后两车相遇.
由题意,得
解得x=9.8.
答:快车开出9.8 h后两车相遇.
探索新知
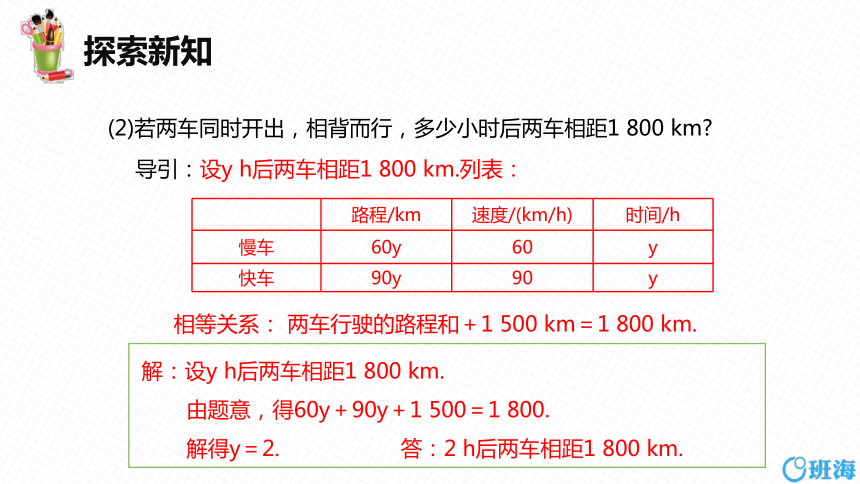
(2)若两车同时开出,相背而行,多少小时后两车相距1 800 km
导引:设y h后两车相距1 800 km.列表:
相等关系: 两车行驶的路程和+1 500 km=1 800 km.
路程/km 速度/(km/h) 时间/h
慢车 60y 60 y
快车 90y 90 y
解:设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800.
解得y=2. 答:2 h后两车相距1 800 km.
探索新知
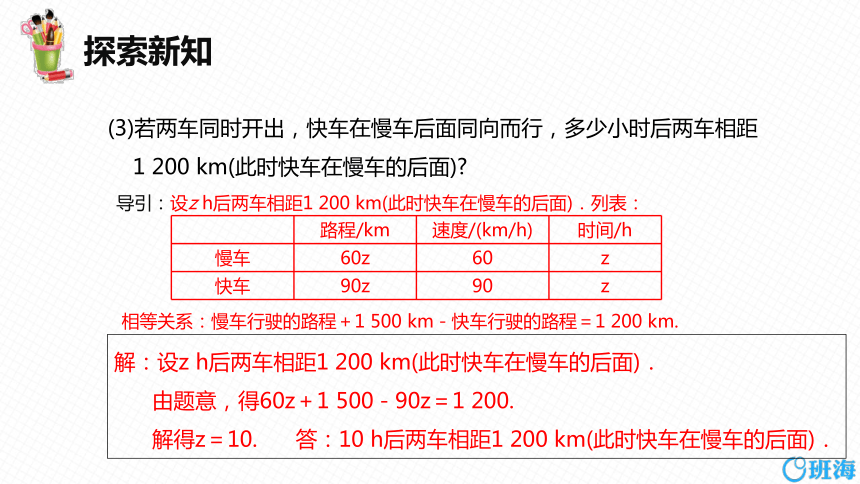
(3)若两车同时开出,快车在慢车后面同向而行,多少小时后两车相距
1 200 km(此时快车在慢车的后面)
导引:设z h后两车相距1 200 km(此时快车在慢车的后面).列表:
相等关系:慢车行驶的路程+1 500 km-快车行驶的路程=1 200 km.
路程/km 速度/(km/h) 时间/h
慢车 60z 60 z
快车 90z 90 z
解:设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200.
解得z=10. 答:10 h后两车相距1 200 km(此时快车在慢车的后面).
探索新知
(1)分析行程问题时,可借助图示、列表来分析数量关系,图示可直观找出路程的
相等关系,列表可将路程、速度、时间的关系清晰地展示出来.
(2)本例是求时间,我们可设时间为未知数,从表中求路程;如果要求的是路程,
那么我们可设路程为未知数,从表中求时间,其依据是路程、速度.和时间三者
间的关系式.如(1)小题若将“几小时后两车相遇?”改为“相遇时快车走了多
少千米?”如间接设未知数,则原解析及解不变,将x求出后,再求出90x的值
即可,如直接设未知数,则解析改为:设相遇时快车走了x km.
总 结
探索新知
路程/km 速度/(km/h) 时间/h
慢车 1 500-x 60
快车 x 90
列表:
相等关系:
方程为
(3)一般规律:在路程、速度、时间这三个量中,甲量已知,从乙量
设元,则从丙量中找相等关系列方程;在所有行程问题中,一般
都已知一个量,另两个量相互之间都存在相等关系.
探索新知
例2 小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步,
小明跑2圈用的时间和他的哥哥跑3圈用的时间相等,两人同时
同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们
两人同时同地反向出发,则经过几秒他们第一次相遇?
导引:设小明的速度为x m/s.列表:
相等关系:小明走的路程=哥哥走的路程-400 m.
路程/m 速度/(m/s) 时间/s
小明 160x x 160
哥哥 160
探索新知
解: 设小明的速度为x m/s,
则他的哥哥的速度为
由题意得
则小明的哥哥的速度为
设经过y s他们第一次相遇.
由题意,得(5+7.5)y=400.解得y=32.
答:经过32 s他们第一次相遇.
解得x=5.
探索新知
(1)本例在求小明及哥哥的速度时,也可设他们两人的速度分别
为2x m/s和3x m/s.
(2)环形运动问题中的相等关系(同 时同地出发):
①同向相遇:第一次相遇快者的路程-第一次相遇慢者的路程=
跑道一圈的长度;
②反向相遇:第一次相遇快者的路程+第一次相遇慢者的路程=
跑道一圈的长度.
总 结
典题精讲
1.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员摁一
下喇叭,4秒后听到回声,这时汽车离山谷多远?已知空气中声音的传
播速度约为340米/秒,设听到回声时,汽车离山谷x米,根据题意,列
出方程为( )
A.2x+4×20=4×340 B.2x-4×72=4×340
C.2x+4×72=4×340 D.2x-4×20=4×340
A
典题精讲
2.张昆早晨去学校共用时15分钟,他跑了一段,走了一段,他跑步的平
均速度是250米/分,步行的平均速度是80米/分,他家与学校的距离
是2 900米,若他跑步的时间为x分钟,则列出的方程是( )
A.
B.80x+250(15-x)=2 900
C.
D.250x+80(15-x)=2 900
D
探索新知
2
知识点
顺流(风)、逆流(风)问题
航行问题中的基本关系式:
顺水(风)速度=静水(风)速度+水(风)速度.
逆水(风)速度=静水(风)速度-水(风)速度.
探索新知
例3 一艘船从甲码头到乙码头顺流而行,用了 2 h; 从乙码头返回甲码
头逆流而行,用了 2.5 h.已知水流的速度是3 km/h,求船在静
水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,
由此填空:
顺流速度________顺流时间________逆流速度 ________逆流时间.
×
=
×
探索新知
解:设船在静水中的平均速度为x km/h,则顺流速度为(x+3)km/h,
逆流 速度为(x-3)km/k.
根据往返路程相等,列得 2(x+3) =2. 5(x-3).
去括号,得2x+6=2.5x-7. 5.
移项及合并同类项,得0. 5x=13. 5.
系数化为1,得x=27. 答:船在静水中的平均速度为27 km/h.
探索新知
例4 一架飞机飞行在两个城市之间,风速为24 km/h,顺风飞行需要
2 h 50 min,逆风飞行需要3 h,求飞机在无风时的平均速度及两
城市之间的距离.
方法一:设速度为未知数.
导引:设飞机在无风时的平均速度为x km/h,
2 h 50 min=
探索新知
相等关系:顺风行驶路程=逆风行驶路程.
路程/km 平均速度/(km/h) 时间/h
顺风飞行 x+24
逆风飞行 3(x-24) x-24 3
列表:
探索新知
解: 2 h 50 min=
设飞机在无风时的平均速度为x km/h,
则顺风速度为(x+24) km/h,
逆风速度为(x-24) km/h.
根据题意,得
解得x=840. 3(x-24)=2 448 .
答:飞机无风时平均速度为840 km/h,两城之间距离为2 448 km.
探索新知
方法二:设路程为未知数.
导引:设两城市之间的距离为x km.列表:
路程/km 平均速度/(km/h) 时间/h
顺风飞行 x
逆风飞行 x 3
相等关系:顺风行驶平均速度-风速=逆风行驶平均速度+风速,
即无风时平均速度相等.
探索新知
解:设两城市之间的距离为x km,则顺风行驶的速度为:
根据题意,得
所以
答:飞机无风时平均速度为840 km/h,两城之间距离为2 448 km.
解得x=2 448.
探索新知
(1)行程问题:虽然不同的问题有不同的关系式,但列表格分析的方式是一致的,在路程、速度、时间这三个量中,已知量相同,设的未知量不同,所列方程也不同.
(2)解有关行程问题时,我们始终要记住一句话:在行程问题三个基本量(路程、速度、时间)中:
总 结
①如果速度已知,若从时间设元,则从路程找相等关系列方程;若从路程设元,则从时间找相等关系列方程;②如果时间已知,若从速度设元,则从路程找相等关系列方程;若从路程设元,则从速度找相等关系列方程;③如果路程已知,若从时间设元,则从速度找相等关系列方程;若从速度设元,则从时间找相等关系列方程.
典题精讲
一架战斗机的贮油量最多够它在空中飞行4.6 h,飞机出航时顺风飞行,在无风时的速度是575 km/h,风速为25 km/h,这架飞机最远能飞出多少千米就应返回?
解: 设飞机顺风飞行的时间为t h.
依题意,有(575+25)t=(575-25)(4.6-t).
解得t=2.2. 则(575+25)t=600×2.2=1 320.
答:这架飞机最远能飞出1 320 km就应返回.
探索新知
3
知识点
上坡、下坡问题
例5 从甲地到乙地的路有一段平路与一段上坡路. 如果骑自行车保持
平路每小时行15 km,上坡路每小时行10 km,下坡路每小时行
18 km,那么从甲地到乙地需29 min,从乙地到甲地需25 min.
从甲地到乙地的路程是多少?
解:设在平路段所用的时间为x小时,
则依题意得: 解得 :
则从甲地到乙地的路程是
答:从甲地到乙地的路程是6.5 km.
典题精讲
家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每小时快1千米;
(2)他上山2小时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1小时.
典题精讲
根据上面信息,他做出如下计划:
(1)在山顶游览1小时;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
典题精讲
解:设上山的速度为v千米/小时,则下山的速度为(v+1)千米/小时,
则2v+1=v+1+2,解得v=2.
即上山的速度是2千米/小时.
则下山的速度是3千米/小时,山高为5千米.
故计划上山的时间为5÷2=2.5(小时),
计划下山的时间为1小时,
则共用时间为2.5+1+1=4.5(小时),
所以出发时间为12:00-4小时30分钟=7:30.
答:孔明同学应该在7点30分从家出发.
学以致用
小试牛刀
1.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员摁
一下喇叭,4秒后听到回声,这时汽车离山谷多远?已知空气中声音
的传播速度约为340米/秒,设听到回声时,汽车离山谷x米,根据题
意,列出方程为( )
A.2x+4×20=4×340 B.2x-4×72=4×340
C.2x+4×72=4×340 D.2x-4×20=4×340
A
小试牛刀
2.一艘船从甲码头到乙码头顺流而行,用了4 h;从乙码头返回甲码头逆
流而行,用了6h.已知水流的速度是2km/h,求船在静水中的平均速度.
解:设船在静水中的速度x千米/小时,
根据往返路程相等,列得4(x+2)=6(x-2),
去括号,得4x+8=6x-12,
移项、合并同类项,得x=10.
答:在静水中的速度10千米/小时.
小试牛刀
3.一架战斗机的贮油量最多够它在空中飞行4.6h,飞机出航时顺风飞行,在无
风时的速度是575Km/h,风速为25Km/h,这架飞机最多飞出多远就应返回
设可顺风飞行X小时
则逆风返回时间为4.6-X小时
X× (575+25)=(4.6-X)×(575-25)
600X=2530-550X
1150X=2530
X=2.2 答:顺风飞行2.2小时后就要返航了.
解:
小试牛刀
4. A、B两地间的距离为360km,甲车从A地出发开往B地,每小时行驶
72km;甲车出发25分钟后,乙车从B地出发开往A地,每小时行驶48
km,两车相遇后,各自仍按原速度、原方向继续行驶,求相遇以后
两车相距100km时,甲车共行驶了多少小时?
设甲车共行驶了x小时,
则:48(x- )+72x=360+100
解得:x=4
答:甲车共行驶了4小时.
解:
小试牛刀
5.甲、乙两列火车的长为144m和180m,甲车比乙车每秒多行4m.两列
火车相向而行,从相遇到全部错开需9s,问两车的速度各是多少?
设乙车每秒行驶xm,则甲车每秒行驶(x+4)m,
根据题意得:9(x+x+4)=144+180,
整理得:2x=32,
解得:x=16,
则甲车每秒行驶20m,乙车每秒行驶16m.
解:
课堂小结
课堂小结
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡应注意运动方向.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.3 解一元一次方程(二)
—去括号与去分母
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
解方程:
新课精讲
探索新知
1
知识点
一般行程问题
1. 行程问题中的基本关系式:
路程=速度×时间,
时间=路程÷速度,
速度=路程÷时间.
探索新知
2. 行程问题中的相等关系:
(1)相遇问题中的相等关系:
①若甲、乙相向而行,甲走的路程+乙走的路程=甲、乙出发点之
间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
(2)追及问题中的相等关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间.
探索新知
例1 甲站和乙站相距1 500 km,一列慢车从甲站开出,速度为60 km/h,一列快车从乙站开出,速度为90 km/h.
(1)若两车相向而行,慢车先开30 min,快车开出几小时后两车相遇?
导引:设快车开出x h后两车相遇.列表:
相等关系:慢车行驶的路程+快车行驶的路程=1 500 km.
路程/km 速度/(km/h) 时间/h
慢车 60
快车 90x 90 x
探索新知
解:设快车开出x h后两车相遇.
由题意,得
解得x=9.8.
答:快车开出9.8 h后两车相遇.
探索新知
(2)若两车同时开出,相背而行,多少小时后两车相距1 800 km
导引:设y h后两车相距1 800 km.列表:
相等关系: 两车行驶的路程和+1 500 km=1 800 km.
路程/km 速度/(km/h) 时间/h
慢车 60y 60 y
快车 90y 90 y
解:设y h后两车相距1 800 km.
由题意,得60y+90y+1 500=1 800.
解得y=2. 答:2 h后两车相距1 800 km.
探索新知
(3)若两车同时开出,快车在慢车后面同向而行,多少小时后两车相距
1 200 km(此时快车在慢车的后面)
导引:设z h后两车相距1 200 km(此时快车在慢车的后面).列表:
相等关系:慢车行驶的路程+1 500 km-快车行驶的路程=1 200 km.
路程/km 速度/(km/h) 时间/h
慢车 60z 60 z
快车 90z 90 z
解:设z h后两车相距1 200 km(此时快车在慢车的后面).
由题意,得60z+1 500-90z=1 200.
解得z=10. 答:10 h后两车相距1 200 km(此时快车在慢车的后面).
探索新知
(1)分析行程问题时,可借助图示、列表来分析数量关系,图示可直观找出路程的
相等关系,列表可将路程、速度、时间的关系清晰地展示出来.
(2)本例是求时间,我们可设时间为未知数,从表中求路程;如果要求的是路程,
那么我们可设路程为未知数,从表中求时间,其依据是路程、速度.和时间三者
间的关系式.如(1)小题若将“几小时后两车相遇?”改为“相遇时快车走了多
少千米?”如间接设未知数,则原解析及解不变,将x求出后,再求出90x的值
即可,如直接设未知数,则解析改为:设相遇时快车走了x km.
总 结
探索新知
路程/km 速度/(km/h) 时间/h
慢车 1 500-x 60
快车 x 90
列表:
相等关系:
方程为
(3)一般规律:在路程、速度、时间这三个量中,甲量已知,从乙量
设元,则从丙量中找相等关系列方程;在所有行程问题中,一般
都已知一个量,另两个量相互之间都存在相等关系.
探索新知
例2 小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步,
小明跑2圈用的时间和他的哥哥跑3圈用的时间相等,两人同时
同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们
两人同时同地反向出发,则经过几秒他们第一次相遇?
导引:设小明的速度为x m/s.列表:
相等关系:小明走的路程=哥哥走的路程-400 m.
路程/m 速度/(m/s) 时间/s
小明 160x x 160
哥哥 160
探索新知
解: 设小明的速度为x m/s,
则他的哥哥的速度为
由题意得
则小明的哥哥的速度为
设经过y s他们第一次相遇.
由题意,得(5+7.5)y=400.解得y=32.
答:经过32 s他们第一次相遇.
解得x=5.
探索新知
(1)本例在求小明及哥哥的速度时,也可设他们两人的速度分别
为2x m/s和3x m/s.
(2)环形运动问题中的相等关系(同 时同地出发):
①同向相遇:第一次相遇快者的路程-第一次相遇慢者的路程=
跑道一圈的长度;
②反向相遇:第一次相遇快者的路程+第一次相遇慢者的路程=
跑道一圈的长度.
总 结
典题精讲
1.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员摁一
下喇叭,4秒后听到回声,这时汽车离山谷多远?已知空气中声音的传
播速度约为340米/秒,设听到回声时,汽车离山谷x米,根据题意,列
出方程为( )
A.2x+4×20=4×340 B.2x-4×72=4×340
C.2x+4×72=4×340 D.2x-4×20=4×340
A
典题精讲
2.张昆早晨去学校共用时15分钟,他跑了一段,走了一段,他跑步的平
均速度是250米/分,步行的平均速度是80米/分,他家与学校的距离
是2 900米,若他跑步的时间为x分钟,则列出的方程是( )
A.
B.80x+250(15-x)=2 900
C.
D.250x+80(15-x)=2 900
D
探索新知
2
知识点
顺流(风)、逆流(风)问题
航行问题中的基本关系式:
顺水(风)速度=静水(风)速度+水(风)速度.
逆水(风)速度=静水(风)速度-水(风)速度.
探索新知
例3 一艘船从甲码头到乙码头顺流而行,用了 2 h; 从乙码头返回甲码
头逆流而行,用了 2.5 h.已知水流的速度是3 km/h,求船在静
水中的平均速度.
分析:一般情况下可以认为这艘船往返的路程相等,
由此填空:
顺流速度________顺流时间________逆流速度 ________逆流时间.
×
=
×
探索新知
解:设船在静水中的平均速度为x km/h,则顺流速度为(x+3)km/h,
逆流 速度为(x-3)km/k.
根据往返路程相等,列得 2(x+3) =2. 5(x-3).
去括号,得2x+6=2.5x-7. 5.
移项及合并同类项,得0. 5x=13. 5.
系数化为1,得x=27. 答:船在静水中的平均速度为27 km/h.
探索新知
例4 一架飞机飞行在两个城市之间,风速为24 km/h,顺风飞行需要
2 h 50 min,逆风飞行需要3 h,求飞机在无风时的平均速度及两
城市之间的距离.
方法一:设速度为未知数.
导引:设飞机在无风时的平均速度为x km/h,
2 h 50 min=
探索新知
相等关系:顺风行驶路程=逆风行驶路程.
路程/km 平均速度/(km/h) 时间/h
顺风飞行 x+24
逆风飞行 3(x-24) x-24 3
列表:
探索新知
解: 2 h 50 min=
设飞机在无风时的平均速度为x km/h,
则顺风速度为(x+24) km/h,
逆风速度为(x-24) km/h.
根据题意,得
解得x=840. 3(x-24)=2 448 .
答:飞机无风时平均速度为840 km/h,两城之间距离为2 448 km.
探索新知
方法二:设路程为未知数.
导引:设两城市之间的距离为x km.列表:
路程/km 平均速度/(km/h) 时间/h
顺风飞行 x
逆风飞行 x 3
相等关系:顺风行驶平均速度-风速=逆风行驶平均速度+风速,
即无风时平均速度相等.
探索新知
解:设两城市之间的距离为x km,则顺风行驶的速度为:
根据题意,得
所以
答:飞机无风时平均速度为840 km/h,两城之间距离为2 448 km.
解得x=2 448.
探索新知
(1)行程问题:虽然不同的问题有不同的关系式,但列表格分析的方式是一致的,在路程、速度、时间这三个量中,已知量相同,设的未知量不同,所列方程也不同.
(2)解有关行程问题时,我们始终要记住一句话:在行程问题三个基本量(路程、速度、时间)中:
总 结
①如果速度已知,若从时间设元,则从路程找相等关系列方程;若从路程设元,则从时间找相等关系列方程;②如果时间已知,若从速度设元,则从路程找相等关系列方程;若从路程设元,则从速度找相等关系列方程;③如果路程已知,若从时间设元,则从速度找相等关系列方程;若从速度设元,则从时间找相等关系列方程.
典题精讲
一架战斗机的贮油量最多够它在空中飞行4.6 h,飞机出航时顺风飞行,在无风时的速度是575 km/h,风速为25 km/h,这架飞机最远能飞出多少千米就应返回?
解: 设飞机顺风飞行的时间为t h.
依题意,有(575+25)t=(575-25)(4.6-t).
解得t=2.2. 则(575+25)t=600×2.2=1 320.
答:这架飞机最远能飞出1 320 km就应返回.
探索新知
3
知识点
上坡、下坡问题
例5 从甲地到乙地的路有一段平路与一段上坡路. 如果骑自行车保持
平路每小时行15 km,上坡路每小时行10 km,下坡路每小时行
18 km,那么从甲地到乙地需29 min,从乙地到甲地需25 min.
从甲地到乙地的路程是多少?
解:设在平路段所用的时间为x小时,
则依题意得: 解得 :
则从甲地到乙地的路程是
答:从甲地到乙地的路程是6.5 km.
典题精讲
家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每小时快1千米;
(2)他上山2小时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1小时.
典题精讲
根据上面信息,他做出如下计划:
(1)在山顶游览1小时;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
典题精讲
解:设上山的速度为v千米/小时,则下山的速度为(v+1)千米/小时,
则2v+1=v+1+2,解得v=2.
即上山的速度是2千米/小时.
则下山的速度是3千米/小时,山高为5千米.
故计划上山的时间为5÷2=2.5(小时),
计划下山的时间为1小时,
则共用时间为2.5+1+1=4.5(小时),
所以出发时间为12:00-4小时30分钟=7:30.
答:孔明同学应该在7点30分从家出发.
学以致用
小试牛刀
1.汽车以72千米/时的速度在公路上行驶,开向寂静的山谷,驾驶员摁
一下喇叭,4秒后听到回声,这时汽车离山谷多远?已知空气中声音
的传播速度约为340米/秒,设听到回声时,汽车离山谷x米,根据题
意,列出方程为( )
A.2x+4×20=4×340 B.2x-4×72=4×340
C.2x+4×72=4×340 D.2x-4×20=4×340
A
小试牛刀
2.一艘船从甲码头到乙码头顺流而行,用了4 h;从乙码头返回甲码头逆
流而行,用了6h.已知水流的速度是2km/h,求船在静水中的平均速度.
解:设船在静水中的速度x千米/小时,
根据往返路程相等,列得4(x+2)=6(x-2),
去括号,得4x+8=6x-12,
移项、合并同类项,得x=10.
答:在静水中的速度10千米/小时.
小试牛刀
3.一架战斗机的贮油量最多够它在空中飞行4.6h,飞机出航时顺风飞行,在无
风时的速度是575Km/h,风速为25Km/h,这架飞机最多飞出多远就应返回
设可顺风飞行X小时
则逆风返回时间为4.6-X小时
X× (575+25)=(4.6-X)×(575-25)
600X=2530-550X
1150X=2530
X=2.2 答:顺风飞行2.2小时后就要返航了.
解:
小试牛刀
4. A、B两地间的距离为360km,甲车从A地出发开往B地,每小时行驶
72km;甲车出发25分钟后,乙车从B地出发开往A地,每小时行驶48
km,两车相遇后,各自仍按原速度、原方向继续行驶,求相遇以后
两车相距100km时,甲车共行驶了多少小时?
设甲车共行驶了x小时,
则:48(x- )+72x=360+100
解得:x=4
答:甲车共行驶了4小时.
解:
小试牛刀
5.甲、乙两列火车的长为144m和180m,甲车比乙车每秒多行4m.两列
火车相向而行,从相遇到全部错开需9s,问两车的速度各是多少?
设乙车每秒行驶xm,则甲车每秒行驶(x+4)m,
根据题意得:9(x+x+4)=144+180,
整理得:2x=32,
解得:x=16,
则甲车每秒行驶20m,乙车每秒行驶16m.
解:
课堂小结
课堂小结
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡应注意运动方向.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
