人教版(新)七上-3.3 解一元一次方程(二)——去括号与去分母 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)七上-3.3 解一元一次方程(二)——去括号与去分母 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
3.3 解一元一次方程(二)
—去括号与去分母
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
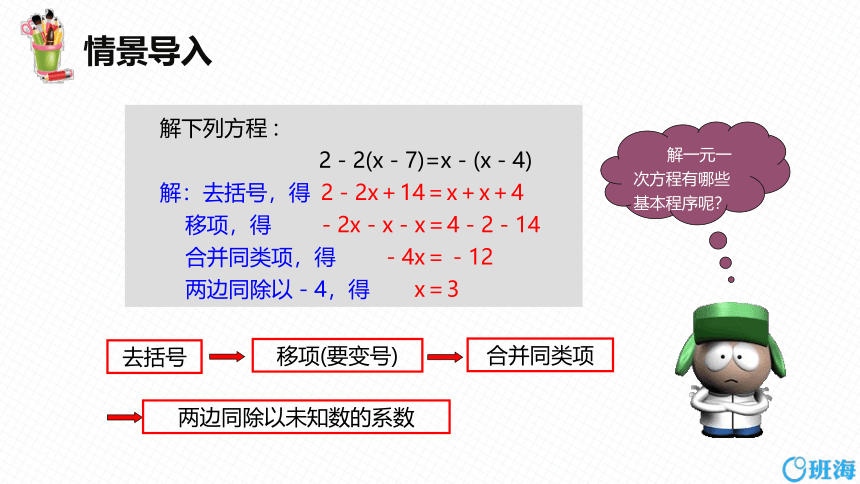
情景导入
解下列方程 :
2-2(x-7)=x-(x-4)
解:去括号,得 2-2x+14=x+x+4
移项,得 -2x-x-x=4-2-14
合并同类项,得 -4x=-12
两边同除以-4,得 x=3
去括号
移项(要变号)
合并同类项
两边同除以未知数的系数
解一元一次方程有哪些基本程序呢?
新课精讲
探索新知
1
知识点
去 分 母
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.
这个问题可以用现在的数学符号表示.设这个数是x,根据题意得方程
当时的埃及人如果采用了这种形式,它一定是“最早”的方程.
问 题
探索新知
思考:如何解上面的方程呢?
解法一:合并同类项(先通分);
解法二:利用等式的基本性质2,两边同乘各分母的最小公倍数.
比较两种解法,哪种更简便?
去分母的方法:方程两边同时乘所有分母的最小公倍数;
去分母的依据:等式的性质2;
去分母的目的:将分数系数转化为整数系数;
去分母的步骤:先找各个分母的最小公倍数,再依据等式的性质2,
将方程两边同时乘这个最小公倍数.
探索新知
例1 把方程 去分母,正确的是( )
A.18x+2(2x-1)=18-3(x+1)
B.3x+2(2x-1)=3-3(x+1)
C.18x+(2x-1)=18-(x+1)
D.18x+4x-1=18-3x+1
导引:此方程所有分母的最小公倍数为6,方程两边都乘6,得
18x+2(2x-1)=18-3(x+1),故选A.
A
探索新知
B选项去分母时漏乘不含分母的项;C选项误认为含分母项的分母恰好都被约去了;D选项忽略了分数线的括号作用; 这三种情况恰是去分母时易出现的错误,因此我们务必高度警惕.
总 结
典题精讲
1.将方程 的两边同乘________可得到3(x+2)=2
(2x+3),这种变形叫________,其依据是__________________.
2.解方程 时,为了去分母应将方程两边同乘( )
A.16 B.12
C.24 D.4
12
去分母
等式的性质2
B
典题精讲
3.在解方程 时,去分母正确的是( )
A.7(1-2x)=3(3x+1)-3
B.1-2x=(3x+1)-3
C.1-2x=(3x+1)-63
D.7(1-2x)=3(3x+1)-63
D
探索新知
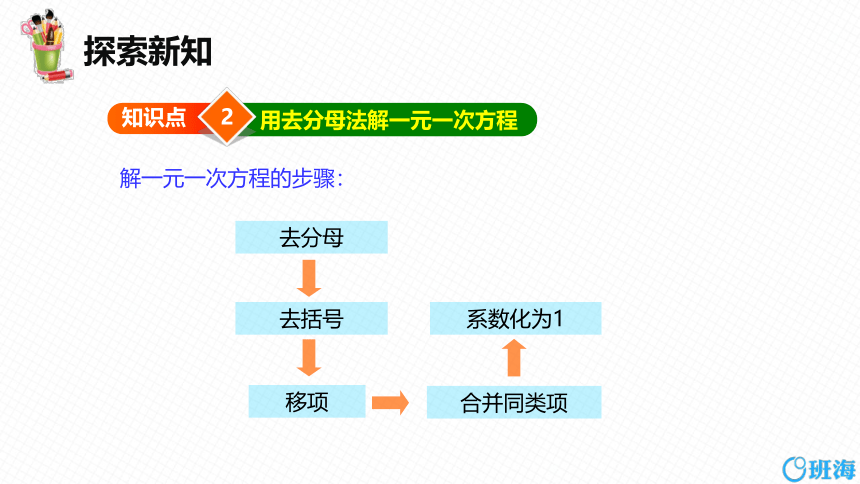
2
知识点
用去分母法解一元一次方程
解一元一次方程的步骤:
移项
合并同类项
系数化为1
去括号
去分母
探索新知
例2 解下列方程:
(1) (2)
解: 去分母(方程两边乘4),得2(x+1)-4=8+(2-x).
去括号,得2x+2-4=8+2-x.
移项,得2x+x=8+2-2+4.
合并同类项,得3x=12.
系数化为1,得x=4.
探索新知
例2 解下列方程:
(2)
解:去分母(方程两边乘6),得18x+3(x-1) =18-2(2x-1).
去括号,得18x+3x-3 =18-4x+2.
移项,得18x+3x+4x = 18+2+3.
合并同类项,得25x=23.
系数化为1,得
探索新知
例3 解方程:
导引:因为3,2,6的最小公倍数是6,所以只需将方程两边同时乘6即可去分母.
解: 去分母,得2(x+5)+24=3(x+3)-(5x-2).
去括号,得2x+10+24=3x+9-5x+2.
移项,得2x-3x+5x=9+2-10-24.
合并同类项,得4x=-23.
系数化为1,得
探索新知
解含分母的一元一次方程的关键是去分母,而去分母的关键是找各个分母的最小公倍数,去分母的方法是将方程两边同时乘这个最小公倍数,解这类方程要经历:去分母→去括号→移项→合并同类项→系数化为1这五步.
总 结
探索新知
例4 解方程:
导引:本例与上例的区别在于分母中含有小数,因此只要将分母的小数转化为整数就可按上例的方法来解了.
解:根据分数的基本性质,得
去分母,得3x-(x-1)=6x-2.
去括号,得3x-x+1=6x-2.
移项,得3x-x-6x=-2-1.
合并同类项,得-4x=-3. 系数化为1,得
探索新知
本例解法体现了转化思想,即将分母中含有小数的方程转化为分母为整数的方程,从而运用分母为整数的方程的解法来解;这里要注意运用分数的基本性质与运用等式的性质2的区别:前者是同一个分数的分子、分母同时乘同一个数;后者是等式两边同时乘同一个数.
总 结
典题精讲
1.下面是解方程 的过程,请在前面的括号内填写变形
步骤,在后面的括号内填写变形依据.
解:原方程可变形为 ( )
去分母,得3(3x+5)=2(2x-1).( )
去括号,得9x+15=4x-2.( )
( ),得9x-4x=-15-2.( )
( ),得5x=-17.
( ),得 ( )
分数的基本性质
等式的性质2
去括号法则
移项
等式的性质1
合并同类项
系数化为1
等式的性质2
典题精讲
2.方程 的解是( )
A.x=1 B.x=2 C.x=4 D.x=6
3.解方程 下面几种解法中,较简便的是( )
A.先两边同乘6 B.先两边同乘5
C.先去括号再移项 D.括号内先通分
B
C
4.解下列方程:
(1) (2)
x=21
x=
学以致用
小试牛刀
1.已知关于x的方程9x-3=kx+14有整数解,那么满足条件的整数
k=___________________.
8,-8,10或26
2.关于x的方程a(x-a)+b(x+b)=0有无穷多个解,则( )
A.a+b=0 B.a-b=0
C.ab=0 D. =0
A
3.关于x的方程(2a+b)x-1=0无解,则ab是( )
A.正数 B.非正数
C.负数 D.非负数
B
小试牛刀
4.已知方程(m-2)x|m|-1+16=0是关于x的一元一次方程,求m的值及
方程的解.
由题意,得
所以m=-2.
将m=-2代入原方程,得-4x+16=0,解得x=4.
解:
小试牛刀
5.已知(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,求式子
199(m+x)(x-2m)+9m+17的值.
由题意,得
所以m=1.
当m=1时,原方程可化为-2x+8=0,解得x=4.
当m=1,x=4时,
199(m+x)(x-2m)+9m+17
=199×5×2+9×1+17=2 016.
解:
小试牛刀
6.解方程:
去分母,得2(4x-1.6)-5(3x-5.4)=10(1.8-x).
去括号、移项、合并同类项,得3x=-5.8.
系数化为1,得x=- .
解:
小试牛刀
化为同分母,得
去分母,得0.1x-0.16+0.5x=0.06.
解得x= .
解:
6.解方程:
小试牛刀
原方程可化为
去分母,得4-6x+0.01=0.01-x.
解得x= .
解:
6.解方程:
小试牛刀
7.小马虎解方程 去分母时,方程右边的-1忘记乘6,
其他步骤都正确,这时方程的解为x=2,试求a的值,并正确解方程.
由题意得4x-2=3x+3a-1,
移项、合并同类项,得x=3a+1.
因为x=2,
所以2=3a+1,则a= .
当a= 时,原方程为
解得x=-3.
解:
课堂小结
课堂小结
步 骤 根 据 注 意 事 项
去分母
去括号
移项
合并同类项
两边同除以未知数的系数
等式性质2
分配率
去括号法则
移项法则
合并同类项法则
等式性质2
1.不要漏乘不含分母的项
2. 分子是多项式应添括号
1.不要漏乘括号中的每一项
2.括号前是“-”号,要变号
移项要变号
系数相加,不漏项
不要把分子、分母搞颠倒
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.3 解一元一次方程(二)
—去括号与去分母
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
解下列方程 :
2-2(x-7)=x-(x-4)
解:去括号,得 2-2x+14=x+x+4
移项,得 -2x-x-x=4-2-14
合并同类项,得 -4x=-12
两边同除以-4,得 x=3
去括号
移项(要变号)
合并同类项
两边同除以未知数的系数
解一元一次方程有哪些基本程序呢?
新课精讲
探索新知
1
知识点
去 分 母
一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.
这个问题可以用现在的数学符号表示.设这个数是x,根据题意得方程
当时的埃及人如果采用了这种形式,它一定是“最早”的方程.
问 题
探索新知
思考:如何解上面的方程呢?
解法一:合并同类项(先通分);
解法二:利用等式的基本性质2,两边同乘各分母的最小公倍数.
比较两种解法,哪种更简便?
去分母的方法:方程两边同时乘所有分母的最小公倍数;
去分母的依据:等式的性质2;
去分母的目的:将分数系数转化为整数系数;
去分母的步骤:先找各个分母的最小公倍数,再依据等式的性质2,
将方程两边同时乘这个最小公倍数.
探索新知
例1 把方程 去分母,正确的是( )
A.18x+2(2x-1)=18-3(x+1)
B.3x+2(2x-1)=3-3(x+1)
C.18x+(2x-1)=18-(x+1)
D.18x+4x-1=18-3x+1
导引:此方程所有分母的最小公倍数为6,方程两边都乘6,得
18x+2(2x-1)=18-3(x+1),故选A.
A
探索新知
B选项去分母时漏乘不含分母的项;C选项误认为含分母项的分母恰好都被约去了;D选项忽略了分数线的括号作用; 这三种情况恰是去分母时易出现的错误,因此我们务必高度警惕.
总 结
典题精讲
1.将方程 的两边同乘________可得到3(x+2)=2
(2x+3),这种变形叫________,其依据是__________________.
2.解方程 时,为了去分母应将方程两边同乘( )
A.16 B.12
C.24 D.4
12
去分母
等式的性质2
B
典题精讲
3.在解方程 时,去分母正确的是( )
A.7(1-2x)=3(3x+1)-3
B.1-2x=(3x+1)-3
C.1-2x=(3x+1)-63
D.7(1-2x)=3(3x+1)-63
D
探索新知
2
知识点
用去分母法解一元一次方程
解一元一次方程的步骤:
移项
合并同类项
系数化为1
去括号
去分母
探索新知
例2 解下列方程:
(1) (2)
解: 去分母(方程两边乘4),得2(x+1)-4=8+(2-x).
去括号,得2x+2-4=8+2-x.
移项,得2x+x=8+2-2+4.
合并同类项,得3x=12.
系数化为1,得x=4.
探索新知
例2 解下列方程:
(2)
解:去分母(方程两边乘6),得18x+3(x-1) =18-2(2x-1).
去括号,得18x+3x-3 =18-4x+2.
移项,得18x+3x+4x = 18+2+3.
合并同类项,得25x=23.
系数化为1,得
探索新知
例3 解方程:
导引:因为3,2,6的最小公倍数是6,所以只需将方程两边同时乘6即可去分母.
解: 去分母,得2(x+5)+24=3(x+3)-(5x-2).
去括号,得2x+10+24=3x+9-5x+2.
移项,得2x-3x+5x=9+2-10-24.
合并同类项,得4x=-23.
系数化为1,得
探索新知
解含分母的一元一次方程的关键是去分母,而去分母的关键是找各个分母的最小公倍数,去分母的方法是将方程两边同时乘这个最小公倍数,解这类方程要经历:去分母→去括号→移项→合并同类项→系数化为1这五步.
总 结
探索新知
例4 解方程:
导引:本例与上例的区别在于分母中含有小数,因此只要将分母的小数转化为整数就可按上例的方法来解了.
解:根据分数的基本性质,得
去分母,得3x-(x-1)=6x-2.
去括号,得3x-x+1=6x-2.
移项,得3x-x-6x=-2-1.
合并同类项,得-4x=-3. 系数化为1,得
探索新知
本例解法体现了转化思想,即将分母中含有小数的方程转化为分母为整数的方程,从而运用分母为整数的方程的解法来解;这里要注意运用分数的基本性质与运用等式的性质2的区别:前者是同一个分数的分子、分母同时乘同一个数;后者是等式两边同时乘同一个数.
总 结
典题精讲
1.下面是解方程 的过程,请在前面的括号内填写变形
步骤,在后面的括号内填写变形依据.
解:原方程可变形为 ( )
去分母,得3(3x+5)=2(2x-1).( )
去括号,得9x+15=4x-2.( )
( ),得9x-4x=-15-2.( )
( ),得5x=-17.
( ),得 ( )
分数的基本性质
等式的性质2
去括号法则
移项
等式的性质1
合并同类项
系数化为1
等式的性质2
典题精讲
2.方程 的解是( )
A.x=1 B.x=2 C.x=4 D.x=6
3.解方程 下面几种解法中,较简便的是( )
A.先两边同乘6 B.先两边同乘5
C.先去括号再移项 D.括号内先通分
B
C
4.解下列方程:
(1) (2)
x=21
x=
学以致用
小试牛刀
1.已知关于x的方程9x-3=kx+14有整数解,那么满足条件的整数
k=___________________.
8,-8,10或26
2.关于x的方程a(x-a)+b(x+b)=0有无穷多个解,则( )
A.a+b=0 B.a-b=0
C.ab=0 D. =0
A
3.关于x的方程(2a+b)x-1=0无解,则ab是( )
A.正数 B.非正数
C.负数 D.非负数
B
小试牛刀
4.已知方程(m-2)x|m|-1+16=0是关于x的一元一次方程,求m的值及
方程的解.
由题意,得
所以m=-2.
将m=-2代入原方程,得-4x+16=0,解得x=4.
解:
小试牛刀
5.已知(m2-1)x2-(m+1)x+8=0是关于x的一元一次方程,求式子
199(m+x)(x-2m)+9m+17的值.
由题意,得
所以m=1.
当m=1时,原方程可化为-2x+8=0,解得x=4.
当m=1,x=4时,
199(m+x)(x-2m)+9m+17
=199×5×2+9×1+17=2 016.
解:
小试牛刀
6.解方程:
去分母,得2(4x-1.6)-5(3x-5.4)=10(1.8-x).
去括号、移项、合并同类项,得3x=-5.8.
系数化为1,得x=- .
解:
小试牛刀
化为同分母,得
去分母,得0.1x-0.16+0.5x=0.06.
解得x= .
解:
6.解方程:
小试牛刀
原方程可化为
去分母,得4-6x+0.01=0.01-x.
解得x= .
解:
6.解方程:
小试牛刀
7.小马虎解方程 去分母时,方程右边的-1忘记乘6,
其他步骤都正确,这时方程的解为x=2,试求a的值,并正确解方程.
由题意得4x-2=3x+3a-1,
移项、合并同类项,得x=3a+1.
因为x=2,
所以2=3a+1,则a= .
当a= 时,原方程为
解得x=-3.
解:
课堂小结
课堂小结
步 骤 根 据 注 意 事 项
去分母
去括号
移项
合并同类项
两边同除以未知数的系数
等式性质2
分配率
去括号法则
移项法则
合并同类项法则
等式性质2
1.不要漏乘不含分母的项
2. 分子是多项式应添括号
1.不要漏乘括号中的每一项
2.括号前是“-”号,要变号
移项要变号
系数相加,不漏项
不要把分子、分母搞颠倒
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
