3.3.2 长方体、正方体体积公式的推导课件 五年级下册数学 人教版(共21张PPT)
文档属性
| 名称 | 3.3.2 长方体、正方体体积公式的推导课件 五年级下册数学 人教版(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 15:49:35 | ||
图片预览




文档简介
(共21张PPT)
长方体、正方体体积公式的推导
长方体和正方体
3
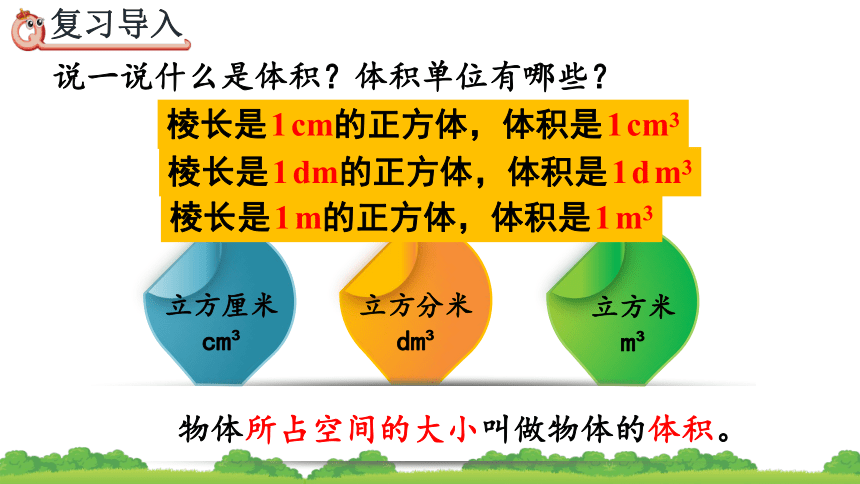
物体所占空间的大小叫做物体的体积。
立方厘米cm
立方分米dm
立方米
m
说一说什么是体积?
体积单位有哪些?
棱长是1cm的正方体,体积是1cm3
棱长是1dm的正方体,体积是1dm3
棱长是1m的正方体,体积是1m3
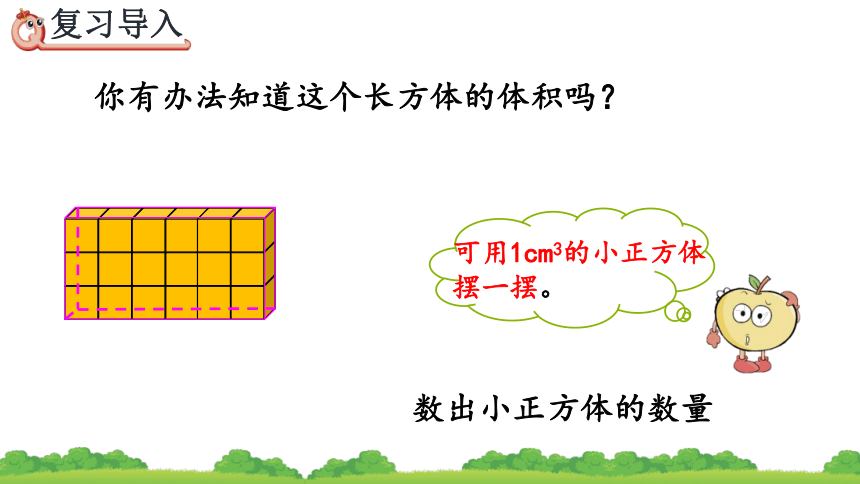
你有办法知道这个长方体的体积吗?
可用1cm3的小正方体摆一摆。
数出小正方体的数量
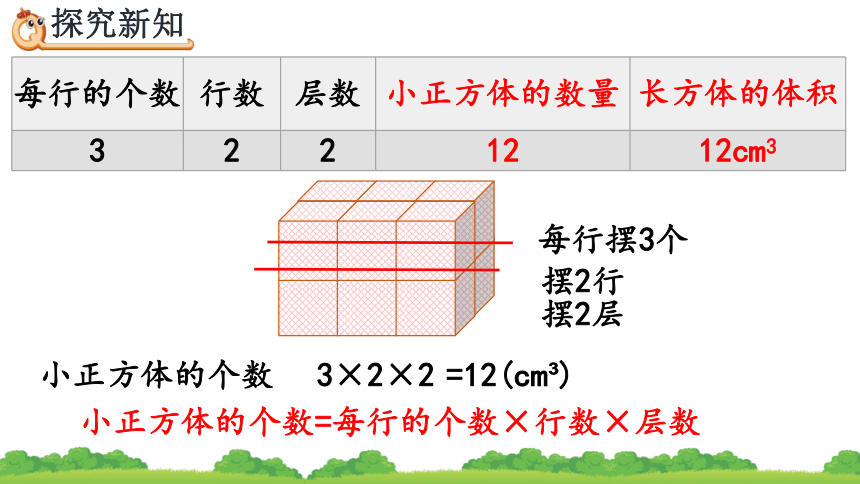
每行的个数 行数 层数 小正方体的数量 长方体的体积
分组实验,验证猜想:用体积为1cm 的小正方体摆长方体,计算小正方体的数量并填写下表。
每行摆3个
用体积为1cm 的小正方体摆长方体,并计算所用小正方体的个数。
摆2行
摆2层
3×2
=12(cm )
×2
小正方体的个数
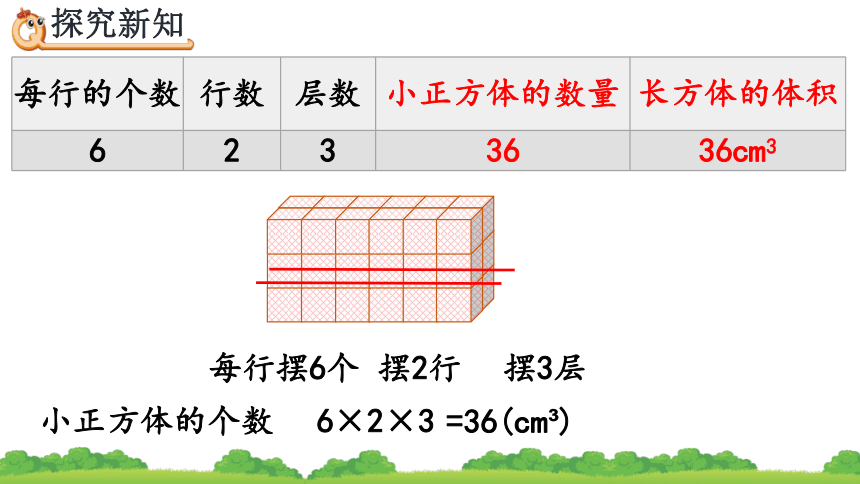
每行的个数 行数 层数 小正方体的数量 长方体的体积
3 2 2 12 12cm3
小正方体的个数=每行的个数×行数×层数
每行摆6个
用体积为1cm 的小正方体摆长方体,并计算所用小正方体的个数。
摆2行
摆3层
6×2
=36(cm )
×3
小正方体的个数
每行的个数 行数 层数 小正方体的数量 长方体的体积
6 2 3 36 36cm3
观察上表,你发现了什么?
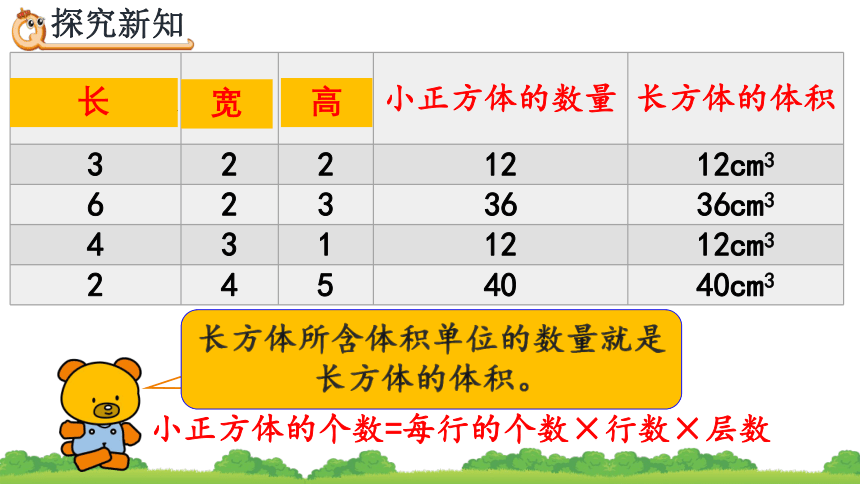
长方体所含体积单位的数量就是长方体的体积。
每行的个数 行数 层数 小正方体的数量 长方体的体积
3 2 2 12 12cm3
6 2 3 36 36cm3
4 3 1 12 12cm3
2 4 5 40 40cm3
长
宽
高
小正方体的个数=每行的个数×行数×层数
小正方体的个数 = 每行的个数×行数×层数
长 宽 高
长方体的体积 = × ×
如果用字母 V 表示长方体的体积,
用 a、b、h 分别表示长方体的长、宽、高。
长方体的体积=长×宽×高
V = abh
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
a
a
a
=a
“a3”
读作“a的立方”,
表示3个a相乘。
正方体是长、宽、高都相等的长方体。
V = a · a · a
“3a”
表示a+a+a,即3个a相加。
64
12
12
64
16
16
计算下面图形的体积。
V=abh
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
判断题:
棱长是6m的正方体的表面积和体积相等。
正方体的表面积=棱长×棱长×6
6×6×6=216(m )
正方体的体积=棱长×棱长×棱长
6×6×6=216(m )
×
表面积和体积是两个不同的概念,单位不一样,不能比较大小。
把一块正方体橡皮泥捏成长方体后,它的形状变了,所以表面积和体积都变了。 ( )
×
形状变了,表面积会变,但体积不变,因为还是那块橡皮泥,所占空间大小没变。
一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的27倍。
1cm
1cm
1cm
假设棱长为1cm,将棱长扩大3倍为:
1×3=3(cm)
正方体的体积=棱长×棱长×棱长
正方体原来的体积为:1×1×1=1(cm )
正方体扩大后的体积为:3×3×3=27(cm )
27÷1=27
√
想一想:长方体和正方体的体积能不能用一个公式来表示呢?
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
与平面接触的这个面叫做底面。
底面
底面
长方体的长和宽相乘就是底面的面积。
长方体或正方体底面的面积叫做底面积。
底面积
底面积
底面积
正方体体积= ×棱长
底面积
长方体体积= ×高
底面积
长(正)方体体积= ×高
=Sh
V
如果用S表示底面积,有:
1.一块长方体肥皂的尺寸如下图,它的体积是多少?
V=abh
=15×7×8
=840(cm3)
答:它的体积是840cm3。
2.一根长方体木料,长 5 m,横截面的面积是 0.06 m2。这根木料的体积是多少?
0.06m2
V = Sh
= 0.06×5
= 0.3(m3)
答:这根木料的体积是 0.3 m3。
0.06m2
5 m
长方体(或正方体)的体积=底面积×高
5 m
这节课你们都学会了哪些知识?
长方体、正方体的体积公式
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
V=a
长方体、正方体体积公式的推导
长方体和正方体
3
物体所占空间的大小叫做物体的体积。
立方厘米cm
立方分米dm
立方米
m
说一说什么是体积?
体积单位有哪些?
棱长是1cm的正方体,体积是1cm3
棱长是1dm的正方体,体积是1dm3
棱长是1m的正方体,体积是1m3
你有办法知道这个长方体的体积吗?
可用1cm3的小正方体摆一摆。
数出小正方体的数量
每行的个数 行数 层数 小正方体的数量 长方体的体积
分组实验,验证猜想:用体积为1cm 的小正方体摆长方体,计算小正方体的数量并填写下表。
每行摆3个
用体积为1cm 的小正方体摆长方体,并计算所用小正方体的个数。
摆2行
摆2层
3×2
=12(cm )
×2
小正方体的个数
每行的个数 行数 层数 小正方体的数量 长方体的体积
3 2 2 12 12cm3
小正方体的个数=每行的个数×行数×层数
每行摆6个
用体积为1cm 的小正方体摆长方体,并计算所用小正方体的个数。
摆2行
摆3层
6×2
=36(cm )
×3
小正方体的个数
每行的个数 行数 层数 小正方体的数量 长方体的体积
6 2 3 36 36cm3
观察上表,你发现了什么?
长方体所含体积单位的数量就是长方体的体积。
每行的个数 行数 层数 小正方体的数量 长方体的体积
3 2 2 12 12cm3
6 2 3 36 36cm3
4 3 1 12 12cm3
2 4 5 40 40cm3
长
宽
高
小正方体的个数=每行的个数×行数×层数
小正方体的个数 = 每行的个数×行数×层数
长 宽 高
长方体的体积 = × ×
如果用字母 V 表示长方体的体积,
用 a、b、h 分别表示长方体的长、宽、高。
长方体的体积=长×宽×高
V = abh
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
a
a
a
=a
“a3”
读作“a的立方”,
表示3个a相乘。
正方体是长、宽、高都相等的长方体。
V = a · a · a
“3a”
表示a+a+a,即3个a相加。
64
12
12
64
16
16
计算下面图形的体积。
V=abh
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
判断题:
棱长是6m的正方体的表面积和体积相等。
正方体的表面积=棱长×棱长×6
6×6×6=216(m )
正方体的体积=棱长×棱长×棱长
6×6×6=216(m )
×
表面积和体积是两个不同的概念,单位不一样,不能比较大小。
把一块正方体橡皮泥捏成长方体后,它的形状变了,所以表面积和体积都变了。 ( )
×
形状变了,表面积会变,但体积不变,因为还是那块橡皮泥,所占空间大小没变。
一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的27倍。
1cm
1cm
1cm
假设棱长为1cm,将棱长扩大3倍为:
1×3=3(cm)
正方体的体积=棱长×棱长×棱长
正方体原来的体积为:1×1×1=1(cm )
正方体扩大后的体积为:3×3×3=27(cm )
27÷1=27
√
想一想:长方体和正方体的体积能不能用一个公式来表示呢?
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
与平面接触的这个面叫做底面。
底面
底面
长方体的长和宽相乘就是底面的面积。
长方体或正方体底面的面积叫做底面积。
底面积
底面积
底面积
正方体体积= ×棱长
底面积
长方体体积= ×高
底面积
长(正)方体体积= ×高
=Sh
V
如果用S表示底面积,有:
1.一块长方体肥皂的尺寸如下图,它的体积是多少?
V=abh
=15×7×8
=840(cm3)
答:它的体积是840cm3。
2.一根长方体木料,长 5 m,横截面的面积是 0.06 m2。这根木料的体积是多少?
0.06m2
V = Sh
= 0.06×5
= 0.3(m3)
答:这根木料的体积是 0.3 m3。
0.06m2
5 m
长方体(或正方体)的体积=底面积×高
5 m
这节课你们都学会了哪些知识?
长方体、正方体的体积公式
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
V=a
