西师大版数学六年级上册第二单元《圆的认识(一)》练习题(含答案)
文档属性
| 名称 | 西师大版数学六年级上册第二单元《圆的认识(一)》练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 86.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览

文档简介
《圆的认识(一)》练习
填空。
1.圆是平面上的一种( )图形。
2.在同圆或等圆中,半径有( )条,直径有( )条。
3.( )决定了圆的位置,( )决定了圆的大小。
4.圆的半径是2cm,那么它的直径是( )。
5.各图中圆的半径和直径分别是多少?
r=( )cm r=( )cm r=( )cm
d=( )cm d=( )cm d=( )cm
选一选。
1.圆内最长的线段是( )
A.半径 B.直径 C.任意一条线段
2.圆的对称轴是( )
A.直径 B.半径 C.直径所在的直线
3.如图圆中是一个正三角形,这个图形的对称轴有( )。
A.1条 B.3条 C.无数条
4.有无数条对称轴的图形是( )。
A.等边三角形 B.正方形 C.圆
用圆规画一个直径为4cm的圆,并标出圆心,半径和直径。
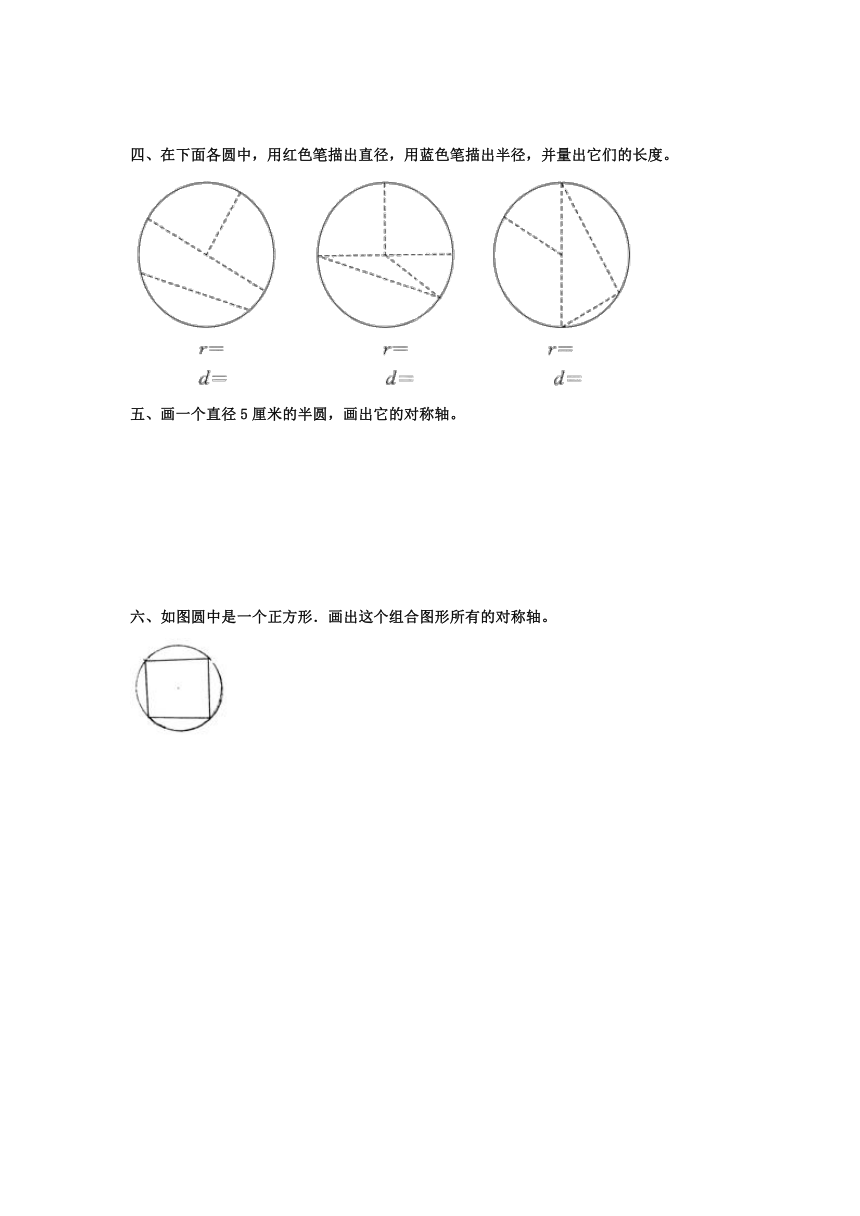
在下面各圆中,用红色笔描出直径,用蓝色笔描出半径,并量出它们的长度。
画一个直径5厘米的半圆,画出它的对称轴。
六、如图圆中是一个正方形.画出这个组合图形所有的对称轴。
解析与答案
一、1.【解析】根据圆的边的特点求解。
【答案】曲线。
2.【解析】根据在同圆或等圆中,半径与直径的特点求解。
【答案】无数;无数。
3.【解析】根据对圆的认识求解。
【答案】圆心;半径。
4.【解析】已知半径,求直径,根据“d=2r”进行解答即可。
【答案】4cm。
5.【解析】(1)2个圆的直径是16,所以圆的半径是16÷2÷2=4厘米;直径是16÷2=8厘米;
(2)圆的直径是16厘米,根据半径是直径的一半,所以圆的半径是16÷2=8厘米;
(3)因为两个圆的半径和是16厘米,所以圆的半径是16÷2=8厘米,直径是8×2=16厘米,据此解答。
【答案】4,8;8,16;8,16。
二、1.【解析】通过圆心并且两端都在圆上的线段叫做直径.通过直径的定义可知,在一个圆中,圆内最长的线段是直径;据此解答。
【答案】B。
2.【解析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可。
【答案】C。
3.【解析】据轴对称图形的意义可得,圆的对称轴有无数条,正三角形的对称轴有3条,所以这两个图形的组合图形只有3条对称轴,分别是这个正三角形的三条对称轴,由此即可选择。
【答案】B。
4.【解析】根据图形的性质结合轴对称的定义即可作出判断。
【答案】C。
三、【解析】由题意知,要画一个直径是4厘米的圆,首先确定圆的半径为4÷2=2厘米,再依据画圆的方法画一个圆,并用字母标出它的圆心O、半径r和直径d即可。
【答案】半径为:4÷2=2(厘米),如图所示:
四、【解析】根据直径和半径的含义:通过圆心,并且两端都在圆上的线段叫做直径;连接圆心和圆上任意一点的线段叫做半径,在图中描出即可。
【答案】
r=1.5厘米 r=1.5厘米 r=1.5厘米
d=3厘米 d=3厘米 d=3厘米
五、【解析】圆心确定圆的位置,半径确定圆的大小,由此以点O为圆心,以5÷2=2.5厘米为半径画半圆,并画出它的对称轴。
【答案】以点O为圆心,以5÷2=2.5厘米为半径画半圆,并画出它的对称轴如图所示:
六、【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,由此即可确定这个图形的对称轴的条数及位置。
【答案】
填空。
1.圆是平面上的一种( )图形。
2.在同圆或等圆中,半径有( )条,直径有( )条。
3.( )决定了圆的位置,( )决定了圆的大小。
4.圆的半径是2cm,那么它的直径是( )。
5.各图中圆的半径和直径分别是多少?
r=( )cm r=( )cm r=( )cm
d=( )cm d=( )cm d=( )cm
选一选。
1.圆内最长的线段是( )
A.半径 B.直径 C.任意一条线段
2.圆的对称轴是( )
A.直径 B.半径 C.直径所在的直线
3.如图圆中是一个正三角形,这个图形的对称轴有( )。
A.1条 B.3条 C.无数条
4.有无数条对称轴的图形是( )。
A.等边三角形 B.正方形 C.圆
用圆规画一个直径为4cm的圆,并标出圆心,半径和直径。
在下面各圆中,用红色笔描出直径,用蓝色笔描出半径,并量出它们的长度。
画一个直径5厘米的半圆,画出它的对称轴。
六、如图圆中是一个正方形.画出这个组合图形所有的对称轴。
解析与答案
一、1.【解析】根据圆的边的特点求解。
【答案】曲线。
2.【解析】根据在同圆或等圆中,半径与直径的特点求解。
【答案】无数;无数。
3.【解析】根据对圆的认识求解。
【答案】圆心;半径。
4.【解析】已知半径,求直径,根据“d=2r”进行解答即可。
【答案】4cm。
5.【解析】(1)2个圆的直径是16,所以圆的半径是16÷2÷2=4厘米;直径是16÷2=8厘米;
(2)圆的直径是16厘米,根据半径是直径的一半,所以圆的半径是16÷2=8厘米;
(3)因为两个圆的半径和是16厘米,所以圆的半径是16÷2=8厘米,直径是8×2=16厘米,据此解答。
【答案】4,8;8,16;8,16。
二、1.【解析】通过圆心并且两端都在圆上的线段叫做直径.通过直径的定义可知,在一个圆中,圆内最长的线段是直径;据此解答。
【答案】B。
2.【解析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可。
【答案】C。
3.【解析】据轴对称图形的意义可得,圆的对称轴有无数条,正三角形的对称轴有3条,所以这两个图形的组合图形只有3条对称轴,分别是这个正三角形的三条对称轴,由此即可选择。
【答案】B。
4.【解析】根据图形的性质结合轴对称的定义即可作出判断。
【答案】C。
三、【解析】由题意知,要画一个直径是4厘米的圆,首先确定圆的半径为4÷2=2厘米,再依据画圆的方法画一个圆,并用字母标出它的圆心O、半径r和直径d即可。
【答案】半径为:4÷2=2(厘米),如图所示:
四、【解析】根据直径和半径的含义:通过圆心,并且两端都在圆上的线段叫做直径;连接圆心和圆上任意一点的线段叫做半径,在图中描出即可。
【答案】
r=1.5厘米 r=1.5厘米 r=1.5厘米
d=3厘米 d=3厘米 d=3厘米
五、【解析】圆心确定圆的位置,半径确定圆的大小,由此以点O为圆心,以5÷2=2.5厘米为半径画半圆,并画出它的对称轴。
【答案】以点O为圆心,以5÷2=2.5厘米为半径画半圆,并画出它的对称轴如图所示:
六、【解析】一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,由此即可确定这个图形的对称轴的条数及位置。
【答案】
