《变化的量》(课件) 六年级下册数学 北师大版(25张PPT)
文档属性
| 名称 | 《变化的量》(课件) 六年级下册数学 北师大版(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 22:17:54 | ||
图片预览






文档简介
(共25张PPT)
量的变化
北师大版数学六年级下册第四单元《正比例与反比例》
1000米赛跑
有哪些变化?
离终点的距离越来越短
已跑路程越多,剩下路程就越少
速度会变化
速度越快,时间越短
心跳越来越快
1
2
像离终点的距离、已跑路程、剩下路程、速度、时间、心跳等,在一定的情境中,发生变化的量,叫做变量。
一个量变化,往往会引起另一个量变化。如已跑路程和剩下路程,速度和时间。
妙想体重记录
出生时,妙想只有3.5千克重,2岁时重14.0千克,4岁时测量结果是18.0千克,6岁时长到了21千克。
年龄 体重/kg
出生时 3.5
2岁 14.0
4岁 18.0
6岁 21.0
6岁前,体重随着年龄的增加而增加
淘气和笑笑分别用表格和图,表示妙想6岁前的体重变化情况
10.5
4
3
先暂停,想一想吧
想一想:有哪些变量?又是如何变化的呢?
淘气说:“在生长过程中,妙想的体重随着年龄的增加而增加”。淘气的说法对吗?
年龄 体重/kg
出生时 3.5
2岁 14.0
4岁 18.0
6岁 21.0
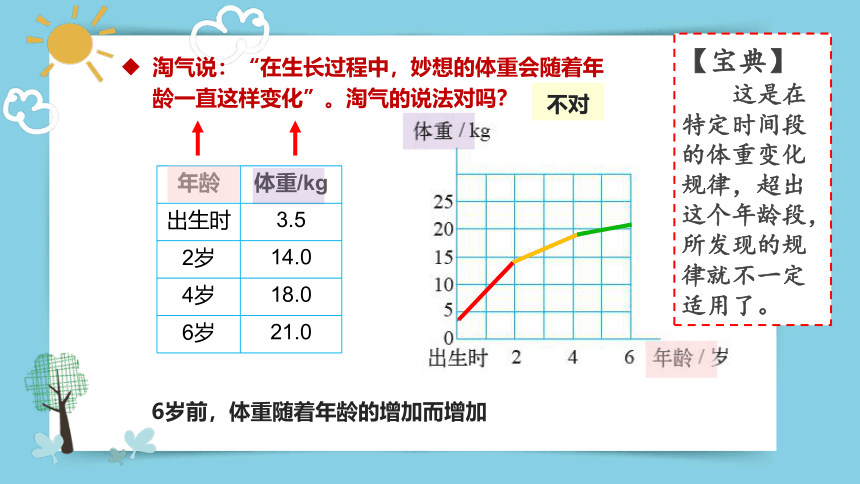
淘气说:“在生长过程中,妙想的体重会随着年龄一直这样变化”。淘气的说法对吗?
6岁前,体重随着年龄的增加而增加
不对
【宝典】
这是在特定时间段的体重变化规律,超出这个年龄段,所发现的规律就不一定适用了。
骆驼,被称为“沙漠之舟” 。体温会随时间的变化而发生较大的变化。
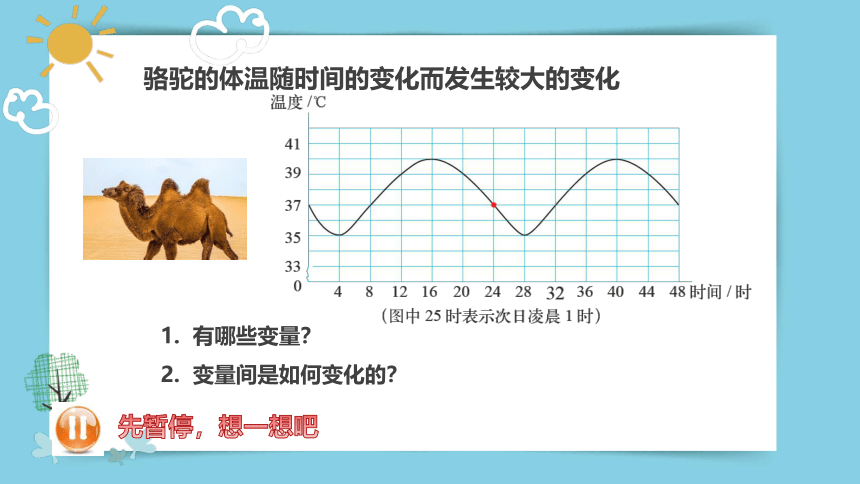
骆驼的体温随时间的变化而发生较大的变化
有哪些变量?
变量间是如何变化的?
先暂停,想一想吧
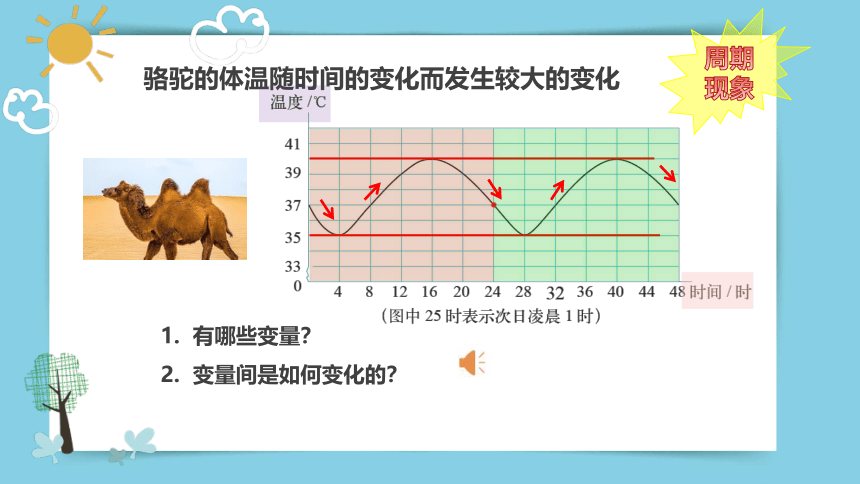
骆驼的体温随时间的变化而发生较大的变化
周期现象
有哪些变量?
变量间是如何变化的?
骆驼的体温随时间的变化而发生较大的变化
(1) 一天中,骆驼体温最高是多少?最低是多少?
周期现象
快问快答
骆驼的体温随时间的变化而发生较大的变化
(2) 一天中,骆驼的体温在什么时间范围内上升?什么时间范围内下降?
周期现象
快问快答
答:骆驼的体温在4时~16时上升,在0时~4时 和 16时~24时 下降。
骆驼的体温随时间的变化而发生较大的变化
(3) 第二天8时骆驼的体温与前一天8时的体温有什么关系?
周期现象
快问快答
(4) 第三天8时骆驼的体温呢?
答:体温一样。
答:第三天8时骆驼体温和第一天8时一样,是37℃ 。
先暂停,想一想吧
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
汽车速度一定时,汽车行驶的路程随着时间的增加而增加
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
看书时,随着已看页数的增加,剩下的页数就减少
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
贪吃蛇的长度随着吃到图形数量的增加而增加
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
股价随着时间的变化而变化
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
【宝典】
相互依存的两个变量,我们称之为相关联的变量。
一种量变化,另一种量也随着变化。
基本练习
李叔叔从家到单位骑自行车的( )和( )是变量。
分析:
速度×时间=路程
路程固定不变
假如路程是15千米
速度是1千米/时,时间是15小时
速度是3千米/时,时间是5小时
速度是5千米/时,时间是3小时
速度
时间
常量
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1. 淘气在一次单元测试中的解题情况(已解题数用x表示,未解题数用y表示)
已解题数 1 5 8 10 12
未解题数 11 7 4 2 0
2. 正方形的边长(a)与周长(C)
3. 正方形的边长(a)与面积(S)
边长/cm 1 2 3 4 …
周长/cm 4 8 12 16 …
边长/cm 1 2 3 4 …
面积/cm 1 4 9 16 …
2
先暂停,想一想吧
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1. 淘气在一次单元测试中的解题情况(已解题数用x表示,未解题数用y表示)
已解题数 1 5 8 10 12
未解题数 11 7 4 2 0
x+y=12
未解题数随着已解题数的增加而减少。
关系表示为:
C=4a
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1×4=4
2×4=8
3×4=12
4×4=16
2. 正方形的边长(a)与周长(C)
正方形的周长随着边长的增加而增加。
a×4=C
周长=边长×4
关系表示为:
边长/cm 1 2 3 4 …
周长/cm 4 8 12 16 …
S=a×a
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1×1=1
2×2=4
3×3=9
4×4=16
正方形的面积随着边长的增加而增加。
a×a=S
面积=边长×边长
关系表示为:
3. 正方形的边长(a)与面积(S)
边长/cm 1 2 3 4 …
面积/cm 1 4 9 16 …
2
课后思考
正方形的边长(a)与周长(C)
正方形的边长(a)与面积(S)
边长/cm 1 2 3 4 …
周长/cm 4 8 12 16 …
边长/cm 1 2 3 4 …
面积/cm 4 8 12 16 …
2
细细观察,发现更多的数学奥秘
正方形的周长随着边长的增加而增加。
正方形的面积随着边长的增加而增加。
课堂总结
变量
常量
(不变的量)
(变化的量)
相关联
无关联
同增同减
一增一减
…
?
?
?
?
(表格、统计图、关系式)
感
谢
聆
听
量的变化
北师大版数学六年级下册第四单元《正比例与反比例》
1000米赛跑
有哪些变化?
离终点的距离越来越短
已跑路程越多,剩下路程就越少
速度会变化
速度越快,时间越短
心跳越来越快
1
2
像离终点的距离、已跑路程、剩下路程、速度、时间、心跳等,在一定的情境中,发生变化的量,叫做变量。
一个量变化,往往会引起另一个量变化。如已跑路程和剩下路程,速度和时间。
妙想体重记录
出生时,妙想只有3.5千克重,2岁时重14.0千克,4岁时测量结果是18.0千克,6岁时长到了21千克。
年龄 体重/kg
出生时 3.5
2岁 14.0
4岁 18.0
6岁 21.0
6岁前,体重随着年龄的增加而增加
淘气和笑笑分别用表格和图,表示妙想6岁前的体重变化情况
10.5
4
3
先暂停,想一想吧
想一想:有哪些变量?又是如何变化的呢?
淘气说:“在生长过程中,妙想的体重随着年龄的增加而增加”。淘气的说法对吗?
年龄 体重/kg
出生时 3.5
2岁 14.0
4岁 18.0
6岁 21.0
淘气说:“在生长过程中,妙想的体重会随着年龄一直这样变化”。淘气的说法对吗?
6岁前,体重随着年龄的增加而增加
不对
【宝典】
这是在特定时间段的体重变化规律,超出这个年龄段,所发现的规律就不一定适用了。
骆驼,被称为“沙漠之舟” 。体温会随时间的变化而发生较大的变化。
骆驼的体温随时间的变化而发生较大的变化
有哪些变量?
变量间是如何变化的?
先暂停,想一想吧
骆驼的体温随时间的变化而发生较大的变化
周期现象
有哪些变量?
变量间是如何变化的?
骆驼的体温随时间的变化而发生较大的变化
(1) 一天中,骆驼体温最高是多少?最低是多少?
周期现象
快问快答
骆驼的体温随时间的变化而发生较大的变化
(2) 一天中,骆驼的体温在什么时间范围内上升?什么时间范围内下降?
周期现象
快问快答
答:骆驼的体温在4时~16时上升,在0时~4时 和 16时~24时 下降。
骆驼的体温随时间的变化而发生较大的变化
(3) 第二天8时骆驼的体温与前一天8时的体温有什么关系?
周期现象
快问快答
(4) 第三天8时骆驼的体温呢?
答:体温一样。
答:第三天8时骆驼体温和第一天8时一样,是37℃ 。
先暂停,想一想吧
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
汽车速度一定时,汽车行驶的路程随着时间的增加而增加
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
看书时,随着已看页数的增加,剩下的页数就减少
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
贪吃蛇的长度随着吃到图形数量的增加而增加
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
股价随着时间的变化而变化
一定情境中,妙想的体重和年龄、骆驼体温和时间,都是两个相互依存的变量,一种量随着另一种量变化而变化。
你还能找出这样的例子吗?
【宝典】
相互依存的两个变量,我们称之为相关联的变量。
一种量变化,另一种量也随着变化。
基本练习
李叔叔从家到单位骑自行车的( )和( )是变量。
分析:
速度×时间=路程
路程固定不变
假如路程是15千米
速度是1千米/时,时间是15小时
速度是3千米/时,时间是5小时
速度是5千米/时,时间是3小时
速度
时间
常量
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1. 淘气在一次单元测试中的解题情况(已解题数用x表示,未解题数用y表示)
已解题数 1 5 8 10 12
未解题数 11 7 4 2 0
2. 正方形的边长(a)与周长(C)
3. 正方形的边长(a)与面积(S)
边长/cm 1 2 3 4 …
周长/cm 4 8 12 16 …
边长/cm 1 2 3 4 …
面积/cm 1 4 9 16 …
2
先暂停,想一想吧
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1. 淘气在一次单元测试中的解题情况(已解题数用x表示,未解题数用y表示)
已解题数 1 5 8 10 12
未解题数 11 7 4 2 0
x+y=12
未解题数随着已解题数的增加而减少。
关系表示为:
C=4a
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1×4=4
2×4=8
3×4=12
4×4=16
2. 正方形的边长(a)与周长(C)
正方形的周长随着边长的增加而增加。
a×4=C
周长=边长×4
关系表示为:
边长/cm 1 2 3 4 …
周长/cm 4 8 12 16 …
S=a×a
提升练习
有哪些变量?变量间是如何变化的?你能用式子表示变量间的关系吗?
1×1=1
2×2=4
3×3=9
4×4=16
正方形的面积随着边长的增加而增加。
a×a=S
面积=边长×边长
关系表示为:
3. 正方形的边长(a)与面积(S)
边长/cm 1 2 3 4 …
面积/cm 1 4 9 16 …
2
课后思考
正方形的边长(a)与周长(C)
正方形的边长(a)与面积(S)
边长/cm 1 2 3 4 …
周长/cm 4 8 12 16 …
边长/cm 1 2 3 4 …
面积/cm 4 8 12 16 …
2
细细观察,发现更多的数学奥秘
正方形的周长随着边长的增加而增加。
正方形的面积随着边长的增加而增加。
课堂总结
变量
常量
(不变的量)
(变化的量)
相关联
无关联
同增同减
一增一减
…
?
?
?
?
(表格、统计图、关系式)
感
谢
聆
听
