3.1.1 第2课时 一元一次方程 课件(共18张PPT)
文档属性
| 名称 | 3.1.1 第2课时 一元一次方程 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 860.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第三章 一元一次方程
3.1.1 一元一次方程
第2课时 一元一次方程
精品同步教学课件
人教版 七年级上
教学目标
1.掌握一元一次方程的定义以及解的概念;
2.学会判断某个数值是不是一元一次方程的解.
3.初步学会如何寻找问题中的等量关系,并列出方程.
重点:掌握一元一次方程的概念
难点:初步学会如何寻找问题中的等量关系,并列出一元一次方程.
核心素养分析:培养抽象能力及模型思想
方程的解
一
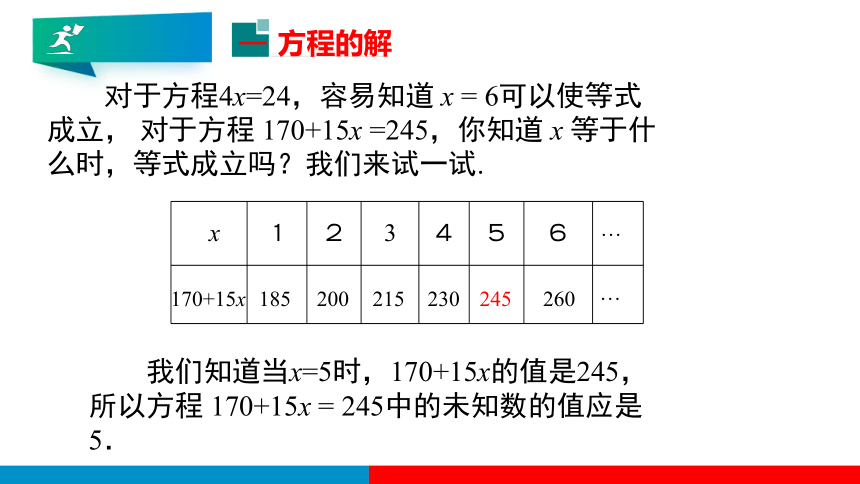
对于方程4x=24,容易知道 x = 6可以使等式成立, 对于方程 170+15x =245,你知道 x 等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程 170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
使方程左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
x=420是 方程的解吗
知识要点
方程的解
特别提醒:方程的解与解方程的关系
(1)方程的解与解方程是两个不同的概念,方程的解是一个结果,是一个具体的数值,而解方程是变形的过程;
(2)方程的解是通过解方程求得的.
例 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
1. 将数值代入方程左边进行计算,
2. 将数值代入方程右边进行计算,
3. 若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
方法归纳
练习. 下列方程中解为x=2 的是( )
A. 2x=6 B. - x=1
C. 2+x=0 D. 2x-1=3
D
练习. 已知y=1 是方程my=y+2 的解,求m2-3m+1 的值.
解:把y=1代入方程my=y+2中得m=3,
当m=3时,m2-3m+1=9-3×3+1=1.
观察下列方程,它们有什么共同点?
70 y=60(y+1)
70(z-1)=60z
观察与思考
问题1 每个方程中,各含有几个未知数?
问题2 说一说每个方程中未知数的次数.
问题3 等号两边的式子有什么共同点?
1个
1次
都是整式
一元一次方程的概念
二
知识要点
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
一元一次方程
下列哪些是一元一次方程?
(1) ; (2) ;
(3) ;(4) ;
(5) ; (6) ;
(7) .
√
√
练一练
例 若关于x的方程 是一元一次方程,则
n 的值为 .
【变式题】加了限制条件,需进行取舍
方程 是关于x的一元一次方程,则
m= .
2或-2
1
典例精析
注:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
1. 下列方程:
; ; ; ;
.
其中是方程的是 ,是一元一次方程的
是 .(填序号)
①②③④⑤
②③
随堂检测
2. 已知方程 是关于x的一元一
次方程,求m的值,并写出其方程.
解:因为方程 是关于x的一元
一次方程,
所以|m|-1 = 1,且m-2≠0,得m = -2.
所以原方程为-4x+3 = -7.
课堂小结
1. 一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两
边都是整式,这样的方程叫做一元一次方程.
https://www.21cnjy.com/help/help_extract.php
第三章 一元一次方程
3.1.1 一元一次方程
第2课时 一元一次方程
精品同步教学课件
人教版 七年级上
教学目标
1.掌握一元一次方程的定义以及解的概念;
2.学会判断某个数值是不是一元一次方程的解.
3.初步学会如何寻找问题中的等量关系,并列出方程.
重点:掌握一元一次方程的概念
难点:初步学会如何寻找问题中的等量关系,并列出一元一次方程.
核心素养分析:培养抽象能力及模型思想
方程的解
一
对于方程4x=24,容易知道 x = 6可以使等式成立, 对于方程 170+15x =245,你知道 x 等于什么时,等式成立吗?我们来试一试.
x 1 2 3 4 5 6 …
…
我们知道当x=5时,170+15x的值是245,所以方程 170+15x = 245中的未知数的值应是5.
185
200
215
230
245
260
170+15x
使方程左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
x=420是 方程的解吗
知识要点
方程的解
特别提醒:方程的解与解方程的关系
(1)方程的解与解方程是两个不同的概念,方程的解是一个结果,是一个具体的数值,而解方程是变形的过程;
(2)方程的解是通过解方程求得的.
例 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解?
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
1. 将数值代入方程左边进行计算,
2. 将数值代入方程右边进行计算,
3. 若左边=右边,则是方程的解,反之,则不是.
判断一个数值是不是方程的解的步骤:
方法归纳
练习. 下列方程中解为x=2 的是( )
A. 2x=6 B. - x=1
C. 2+x=0 D. 2x-1=3
D
练习. 已知y=1 是方程my=y+2 的解,求m2-3m+1 的值.
解:把y=1代入方程my=y+2中得m=3,
当m=3时,m2-3m+1=9-3×3+1=1.
观察下列方程,它们有什么共同点?
70 y=60(y+1)
70(z-1)=60z
观察与思考
问题1 每个方程中,各含有几个未知数?
问题2 说一说每个方程中未知数的次数.
问题3 等号两边的式子有什么共同点?
1个
1次
都是整式
一元一次方程的概念
二
知识要点
这样的方程叫做一元一次方程.
等号两边都是整式,
(一次)
只含有一个未知数,
(一元)
未知数的次数都是1,
一元一次方程
下列哪些是一元一次方程?
(1) ; (2) ;
(3) ;(4) ;
(5) ; (6) ;
(7) .
√
√
练一练
例 若关于x的方程 是一元一次方程,则
n 的值为 .
【变式题】加了限制条件,需进行取舍
方程 是关于x的一元一次方程,则
m= .
2或-2
1
典例精析
注:一元一次方程中求字母的值,需谨记两个条件:
①未知数的次数为1;②未知数的系数不为0.
1. 下列方程:
; ; ; ;
.
其中是方程的是 ,是一元一次方程的
是 .(填序号)
①②③④⑤
②③
随堂检测
2. 已知方程 是关于x的一元一
次方程,求m的值,并写出其方程.
解:因为方程 是关于x的一元
一次方程,
所以|m|-1 = 1,且m-2≠0,得m = -2.
所以原方程为-4x+3 = -7.
课堂小结
1. 一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两
边都是整式,这样的方程叫做一元一次方程.
https://www.21cnjy.com/help/help_extract.php
