3.1.2第1课时等式的性质 课件(共21页)
文档属性
| 名称 | 3.1.2第1课时等式的性质 课件(共21页) |  | |
| 格式 | zip | ||
| 文件大小 | 975.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 13:46:55 | ||
图片预览






文档简介
(共21张PPT)
第三章 一元一次方程
3.1 从算式到方程
3.1.2 第1课时 等式的性质
精品同步教学课件
教学目标
1. 理解、掌握等式的性质.
2. 能正确运用等式的性质解决简单的问题.
重点:理解、掌握等式的性质.
难点:能正确运用等式的性质解决简单的问题.
核心素养分析:培养抽象能力及运算能力
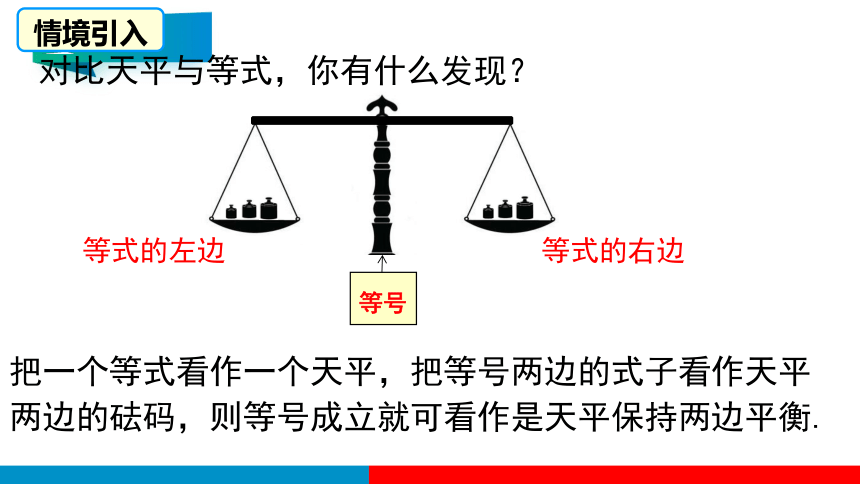
对比天平与等式,你有什么发现?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
等号
等式的左边
等式的右边
情境引入
√
√
√
√
√
下列各式中哪些是等式?
; ; ;④ 3;
;⑥2+3=5;⑦3×4=12;⑧9x+10=19;
; .
用等号表示相等关系的式子叫做等式. 我们可以用
a=b表示一般的等式.
等式的性质
一
观察与思考
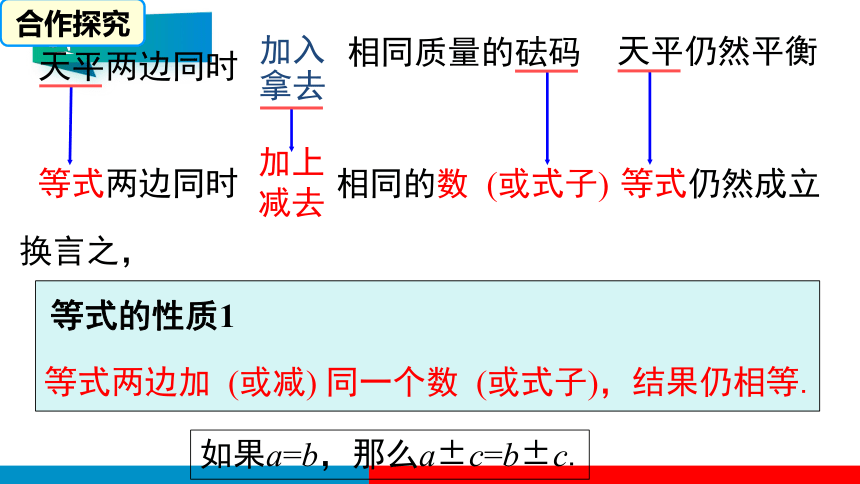
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数 (或式子)
等式两边同时
加上
减去
等式仍然成立
换言之,
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
合作探究
等式的性质1
由天平看等式的性质2
等式两边乘同一个数,或除以同一个不为0的数,结
果仍相等.
等式的性质2
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
等式的性质
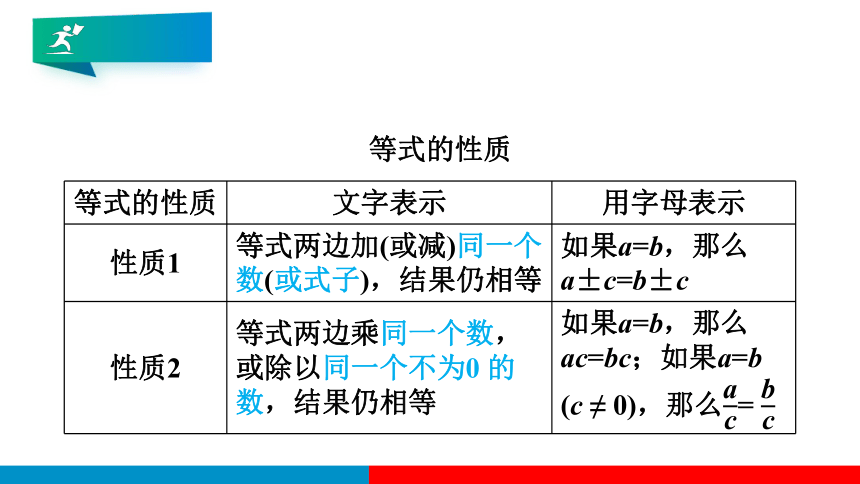
等式的性质 文字表示 用字母表示
性质1 等式两边加(或减)同一个数(或式子),结果仍相等 如果a=b,那么a±c=b±c
性质2 等式两边乘同一个数,或除以同一个不为0 的数,结果仍相等 如果a=b,那么ac=bc;如果a=b
(c ≠ 0),那么=
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b
(2) 从 a+2=b+2 能不能得到 a=b,为什么
(3) 从-3a=-3b 能不能得到 a=b,为什么
(4) 从 3ac=4a 能不能得到 3c=4,为什么
(1) 从 x = y 能不能得到 ,为什么
能,根据等式的性质2,两边同时除以9或乘1/9
能,根据等式的性质1,两边同时减2
能,根据等式的性质2,两边同时除以-3
不能,a可能为0
例2 已知mx=my,下列结论错误的是 ( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
解析:根据等式的性质1,可知B、C正确;根据等式的性质2,可知D正确;根据等式的性质2,A选项只有m≠0时才成立,故A错误,故选A.
A
练习1. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
B
练习2:填空
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是
根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得
到 x = -2,这是根据等式性质 ___;
加3
1
2
2
下列变形不正确的是( )
A. 若a=b,则2a=a+b B. 若a=b,则a-b=0
C. 若= ,则a=b D. 若ac=bc,则a=b
例 3
解题秘方:依据等式的两条性质进行辨析.
答案:D
解:选项A的变形是利用等式的性质1,两边同加a,故正确;
选项B的变形是利用等式的性质1,两边同减b,故正确;
选项C的变形是利用等式的性质2,两边同乘c,故正确;
选项D的变形是利用等式的性质2,两边同除以c,没有说明c ≠ 0,故D的变形是错误的.
练习. 已知等式3x=2y+3,则下列变形不一定成立的是( )
A. 3x-3=2y
B. x= y+1
C. 3x+1=2y+4
D. 3xz=2yz+3
D
A
2. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
1. 下列说法正确的是( )
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
B
课堂小结
等式的
基本性质
基本性质1
基本性质2
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
https://www.21cnjy.com/help/help_extract.php
第三章 一元一次方程
3.1 从算式到方程
3.1.2 第1课时 等式的性质
精品同步教学课件
教学目标
1. 理解、掌握等式的性质.
2. 能正确运用等式的性质解决简单的问题.
重点:理解、掌握等式的性质.
难点:能正确运用等式的性质解决简单的问题.
核心素养分析:培养抽象能力及运算能力
对比天平与等式,你有什么发现?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
等号
等式的左边
等式的右边
情境引入
√
√
√
√
√
下列各式中哪些是等式?
; ; ;④ 3;
;⑥2+3=5;⑦3×4=12;⑧9x+10=19;
; .
用等号表示相等关系的式子叫做等式. 我们可以用
a=b表示一般的等式.
等式的性质
一
观察与思考
观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
相同的数 (或式子)
等式两边同时
加上
减去
等式仍然成立
换言之,
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果a=b,那么a±c=b±c.
合作探究
等式的性质1
由天平看等式的性质2
等式两边乘同一个数,或除以同一个不为0的数,结
果仍相等.
等式的性质2
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
等式的性质
等式的性质 文字表示 用字母表示
性质1 等式两边加(或减)同一个数(或式子),结果仍相等 如果a=b,那么a±c=b±c
性质2 等式两边乘同一个数,或除以同一个不为0 的数,结果仍相等 如果a=b,那么ac=bc;如果a=b
(c ≠ 0),那么=
(2) 怎样从等式 3+x=1 得到等式 x =-2
(3) 怎样从等式 4x=12 得到等式 x =3
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
例1 (1) 怎样从等式 x-5= y-5 得到等式 x = y
依据等式的性质1两边同时加5.
(4) 怎样从等式 得到等式 a = b
(2) 从 a+2=b+2 能不能得到 a=b,为什么
(3) 从-3a=-3b 能不能得到 a=b,为什么
(4) 从 3ac=4a 能不能得到 3c=4,为什么
(1) 从 x = y 能不能得到 ,为什么
能,根据等式的性质2,两边同时除以9或乘1/9
能,根据等式的性质1,两边同时减2
能,根据等式的性质2,两边同时除以-3
不能,a可能为0
例2 已知mx=my,下列结论错误的是 ( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
解析:根据等式的性质1,可知B、C正确;根据等式的性质2,可知D正确;根据等式的性质2,A选项只有m≠0时才成立,故A错误,故选A.
A
练习1. 下列变形,正确的是 ( )
A. 若ac = bc,则a = b
B. 若 ,则a = b
C. 若a2 = b2,则a = b
D. 若 ,则x = -2
B
练习2:填空
(1) 将等式x-3=5 的两边都_____得到x =8 ,这是
根据等式的性质__;
(2) 将等式 的两边都乘以___或除以 ___得
到 x = -2,这是根据等式性质 ___;
加3
1
2
2
下列变形不正确的是( )
A. 若a=b,则2a=a+b B. 若a=b,则a-b=0
C. 若= ,则a=b D. 若ac=bc,则a=b
例 3
解题秘方:依据等式的两条性质进行辨析.
答案:D
解:选项A的变形是利用等式的性质1,两边同加a,故正确;
选项B的变形是利用等式的性质1,两边同减b,故正确;
选项C的变形是利用等式的性质2,两边同乘c,故正确;
选项D的变形是利用等式的性质2,两边同除以c,没有说明c ≠ 0,故D的变形是错误的.
练习. 已知等式3x=2y+3,则下列变形不一定成立的是( )
A. 3x-3=2y
B. x= y+1
C. 3x+1=2y+4
D. 3xz=2yz+3
D
A
2. 下列各式变形正确的是 ( )
A. 由3x-1= 2x+1得3x-2x =1+1
B. 由5+1= 6得5= 6+1
C. 由2(x+1) = 2y+1得x +1= y +1
D. 由2a + 3b = c-6 得2a = c-18b
1. 下列说法正确的是( )
A. 等式都是方程
B. 方程都是等式
C. 不是方程的就不是等式
D. 未知数的值就是方程的解
B
课堂小结
等式的
基本性质
基本性质1
基本性质2
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
https://www.21cnjy.com/help/help_extract.php
