3.1.2第2课时利用等式的性质解方程 课件(共20页)
文档属性
| 名称 | 3.1.2第2课时利用等式的性质解方程 课件(共20页) |  | |
| 格式 | zip | ||
| 文件大小 | 965.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-20 13:46:55 | ||
图片预览








文档简介
(共20张PPT)
第三章 一元一次方程
3.1 从算式到方程
3.1.2 第2课时 等式的性质解方程
精品同步教学课件
教学目标
1. 理解、掌握等式的性质.
2. 能正确应用等式的性质解简单的一元一次方程.
重点:理解、掌握等式的性质.
难点:能正确应用等式的性质解简单的一元一次方程.
核心素养分析:培养抽象能力及运算能力
利用等式的性质解方程
一
例1 利用等式的性质解下列方程:
(1) x + 7 = 26
(2) -5x = 20
(3)
(1) x + 7 = 26
解:
得
方程两边同时减7,
x + 7 = 26
-7
-7
于是 =
x
19
小结:解一元一次方程要“化归”为“ x=a ”的形式.
两边同时除以-5,
得
解:
方程
(2) -5x = 20
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
化简,得
x=-4
-5x÷(-5)= 20 ÷(-5)
解:方程两边同时加上5,得
化简,得
方程两边同时
乘 -3,
得 x =
-27
x=-27是原方程的解吗
思考:对比(1),(3)有什么新特点 ?
(3)
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
解:(1)两边同时减6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加-1,得
两边同时乘-3,得x=9.
利用等式的性质解方程.
(1)3x-2=7;
(2)x+3= x -1.
例2
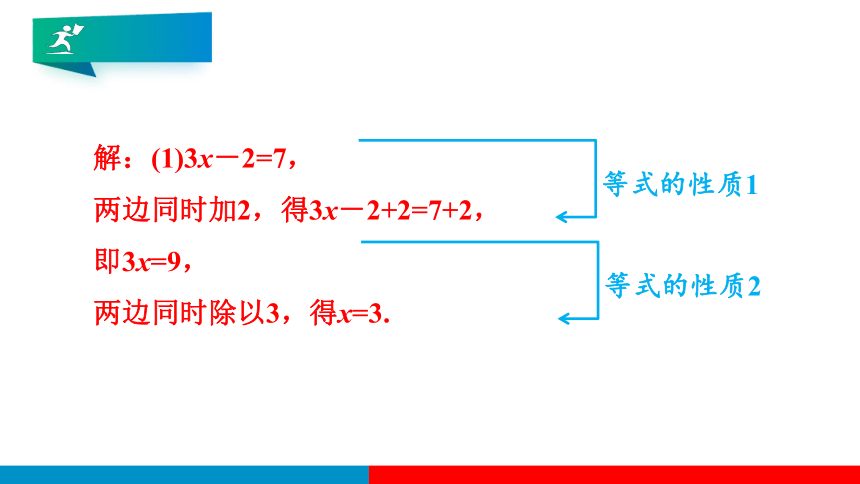
解:(1)3x-2=7,
两边同时加2,得3x-2+2=7+2,
即3x=9,
两边同时除以3,得x=3.
等式的性质1
等式的性质2
(2) x+3= x-1,
两边同时减3,得x+3-3= x-1-3,
即x= x-4,
两边同时减x,得x- x= x-4- x,
即- x=-4,
两边同时除以- ,得x=-4÷ ,即x=24.
等式的性质1
等式的性质1
等式的
性质2
练习. 下列方程的变形,符合等式的性质的是( )
A. 由2x-3=7 得2x=7-3
B. 由2x-3=x-1 得2x -x =1-3
C. 由-3x=5 得x=5+3
D. 由-x=1 得x=-4
D
用合并同类项进行化简:
(1) 3x -5x = ________;
(2) -3x + 7x = ________;
(3) y + 5y- 2y =________;
(4) _______.
-2x
4x
4y
- y
利用合并同类项解简单的一元一次方程
二
x + 2x + 4x = 140
解方程.
分析:解方程,就是把方程变形,化归为 x = m (m为常数)的形式.
合并同类项
系数化为1
依据:乘法对加法的分配律
依据:等式性质2
典例精析
例1 解下列方程:
(1)
(2) .
解:合并同类项,得
系数化为1,得
(1) ;
(2) .
解:合并同类项,得
系数化为1,得
解下列方程:
(1) 5x-2x = 9; (2) .
解:(1)合并同类项,得
3x=9,
系数化为1,得
x=3.
(2)合并同类项,得
2x=7,
练一练
系数化为1,得
https://www.21cnjy.com/help/help_extract.php
第三章 一元一次方程
3.1 从算式到方程
3.1.2 第2课时 等式的性质解方程
精品同步教学课件
教学目标
1. 理解、掌握等式的性质.
2. 能正确应用等式的性质解简单的一元一次方程.
重点:理解、掌握等式的性质.
难点:能正确应用等式的性质解简单的一元一次方程.
核心素养分析:培养抽象能力及运算能力
利用等式的性质解方程
一
例1 利用等式的性质解下列方程:
(1) x + 7 = 26
(2) -5x = 20
(3)
(1) x + 7 = 26
解:
得
方程两边同时减7,
x + 7 = 26
-7
-7
于是 =
x
19
小结:解一元一次方程要“化归”为“ x=a ”的形式.
两边同时除以-5,
得
解:
方程
(2) -5x = 20
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
化简,得
x=-4
-5x÷(-5)= 20 ÷(-5)
解:方程两边同时加上5,得
化简,得
方程两边同时
乘 -3,
得 x =
-27
x=-27是原方程的解吗
思考:对比(1),(3)有什么新特点 ?
(3)
(1) x+6 = 17 ;
(2) -3x = 15 ;
(4)
(3) 2x-1 = -3 ;
解:(1)两边同时减6,得x=11.
(2)两边同时除以-3,得x=-5.
(3)两边同时加1,得2x=-2.
两边同时除以2,得x=-1.
(4)两边同时加-1,得
两边同时乘-3,得x=9.
利用等式的性质解方程.
(1)3x-2=7;
(2)x+3= x -1.
例2
解:(1)3x-2=7,
两边同时加2,得3x-2+2=7+2,
即3x=9,
两边同时除以3,得x=3.
等式的性质1
等式的性质2
(2) x+3= x-1,
两边同时减3,得x+3-3= x-1-3,
即x= x-4,
两边同时减x,得x- x= x-4- x,
即- x=-4,
两边同时除以- ,得x=-4÷ ,即x=24.
等式的性质1
等式的性质1
等式的
性质2
练习. 下列方程的变形,符合等式的性质的是( )
A. 由2x-3=7 得2x=7-3
B. 由2x-3=x-1 得2x -x =1-3
C. 由-3x=5 得x=5+3
D. 由-x=1 得x=-4
D
用合并同类项进行化简:
(1) 3x -5x = ________;
(2) -3x + 7x = ________;
(3) y + 5y- 2y =________;
(4) _______.
-2x
4x
4y
- y
利用合并同类项解简单的一元一次方程
二
x + 2x + 4x = 140
解方程.
分析:解方程,就是把方程变形,化归为 x = m (m为常数)的形式.
合并同类项
系数化为1
依据:乘法对加法的分配律
依据:等式性质2
典例精析
例1 解下列方程:
(1)
(2) .
解:合并同类项,得
系数化为1,得
(1) ;
(2) .
解:合并同类项,得
系数化为1,得
解下列方程:
(1) 5x-2x = 9; (2) .
解:(1)合并同类项,得
3x=9,
系数化为1,得
x=3.
(2)合并同类项,得
2x=7,
练一练
系数化为1,得
https://www.21cnjy.com/help/help_extract.php
