北师大版九年级上册1.2.2矩形的性质与判定课件(共21张PPT)
文档属性
| 名称 | 北师大版九年级上册1.2.2矩形的性质与判定课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 372.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
1.2.2矩形的性质与判定
生活很难,但愿你能全力以赴,做那个最好的自己,独立而勇敢,可爱也善良,对未来充满希望。
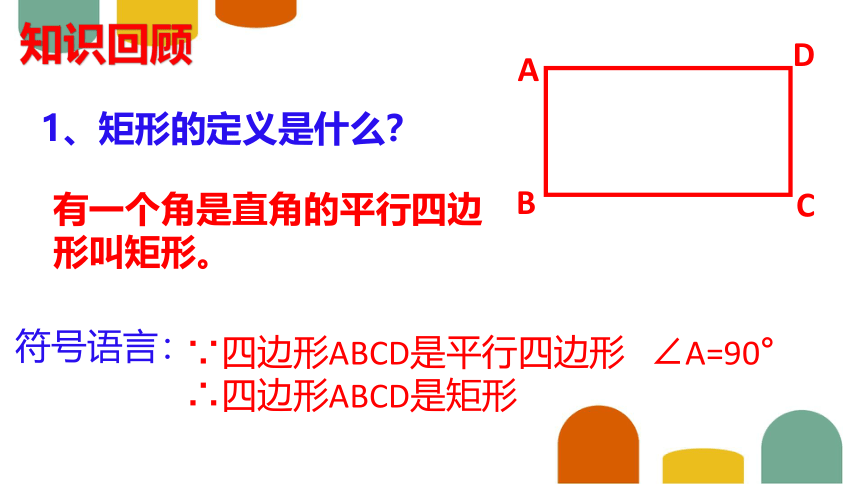
有一个角是直角的平行四边形叫矩形。
知识回顾
1、矩形的定义是什么?
符号语言:
∵四边形ABCD是平行四边形 ∠A=90°
∴四边形ABCD是矩形
A
B
C
D
矩形既是轴对称图形,又是中心对称图形。
2、矩形有哪些性质
边:
角:
对角线:
对称性:
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分;
知识回顾
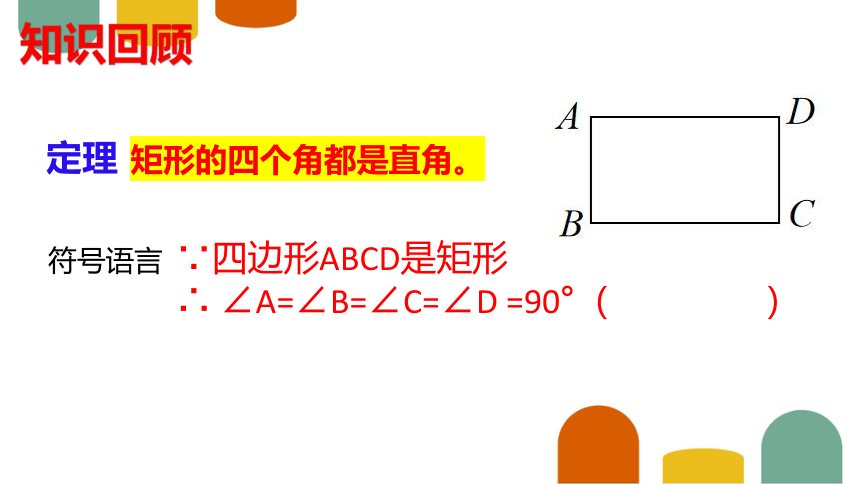
定理
符号语言
∵四边形ABCD是矩形
∴ ∠A=∠B=∠C=∠D =90°( )
矩形的四个角都是直角。
知识回顾
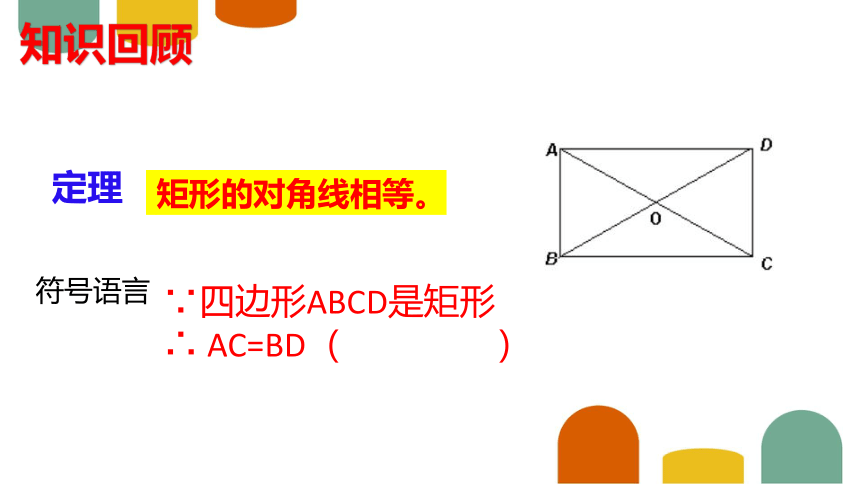
定理
∵四边形ABCD是矩形
∴ AC=BD( )
符号语言
矩形的对角线相等。
知识回顾
符号语言
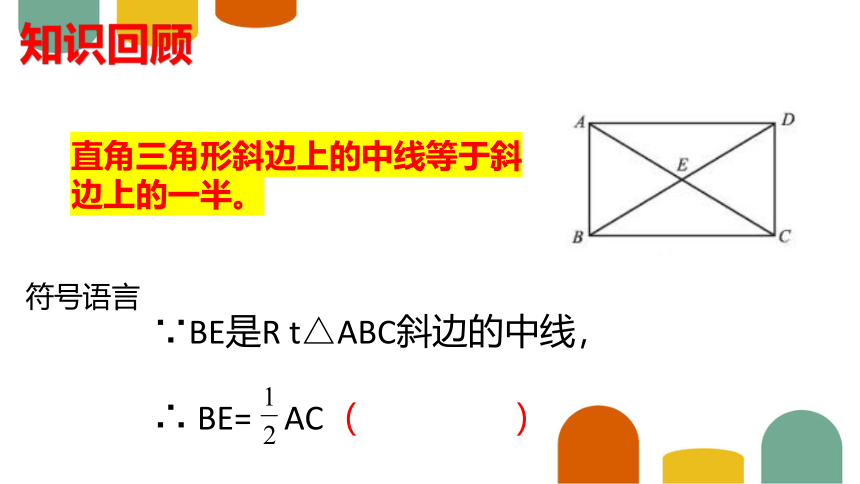
直角三角形斜边上的中线等于斜边上的一半。
∵BE是R t△ABC斜边的中线,
∴ BE= AC( )
知识回顾
情景导入
现在仅有一根较长的绳子做工具,检查一下我们班级的门框(四边在同一平面上)是不是矩形,你有什么办法?
新知探究
你会判定一个平行四边形是矩形吗?
有一角是直角的平行四边形叫做矩形.
∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
符号语言
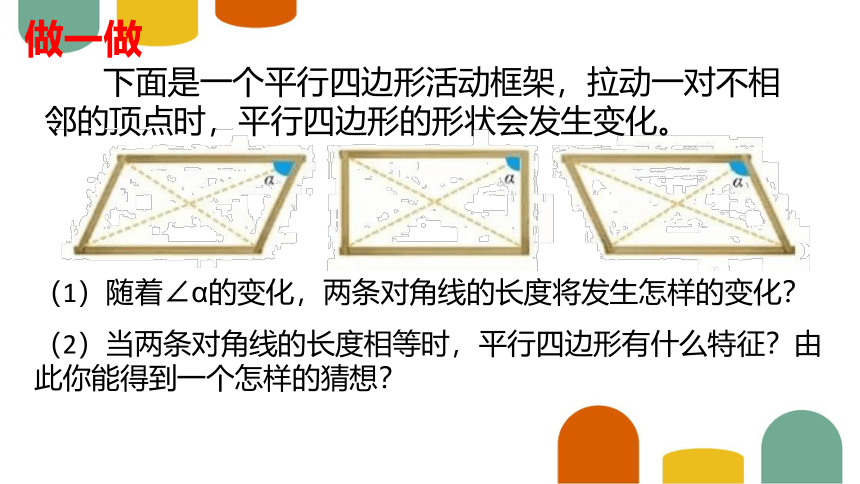
做一做
下面是一个平行四边形活动框架,拉动一对不相邻的顶点时,平行四边形的形状会发生变化。
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
(2)当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
对角线相等的平行四边形是矩形。
猜测与证明
已知:如图,在□ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:□ABCD是矩形.
证明:∵四边形ABCD是平行四边形
∴AB = DC AB∥ DC
又∵BC = CB,AC = DB,
∴△ABC≌△DCB
∴∠ABC = ∠DCB.
∵AB∥ DC
∴∠ABC + ∠DCB = 180°
∴ ∠ABC = 90°
∴ □ ABCD是矩形(矩形的定义)
对角线相等的平行四边形是矩形
定理
符号语言
∵四边形ABCD是平行四边形
又∵AC=BD
∴四边形ABCD是矩形( )
检验门框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则门框一定是矩形,你现在知道为什么了吗?
数学来源于生活
对角线相等的平行四边形是矩形
想一想
我们知道,矩形的四个角都是直角。反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形了呢?请证明你的结论,并与同伴交流。
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
有三个角是直角的四边形是矩形。
猜测与证明
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
有三个角是直角的四边形是矩形。
定理
符号语言
∵在四边形ABCD中,∠A=∠B=∠C=90°
∴四边形ABCD是矩形( )
A
B
C
D
典例精析
例2:如图在□ABCD中,对角线AC和BD相较于点O,△ABO是等边三角形,AB=4.
求□ABCD的面积.
A
B
C
D
O
先独立思考,自己写下过程,小组之间交流对答案或者参考课本例2
1、已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.
求证:四边形ABCD是矩形.
当堂检测
2、已知:如图,菱形ABCD中,对角线AC 和BD 相较于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
当堂检测
当堂检测
3、在三角形ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE,CE.
(1)试判断四边形ABEC的形状。
(2)当三角形ABC满足什么条件时,四边形ABEC是矩形?
1.2.2矩形的性质与判定
生活很难,但愿你能全力以赴,做那个最好的自己,独立而勇敢,可爱也善良,对未来充满希望。
有一个角是直角的平行四边形叫矩形。
知识回顾
1、矩形的定义是什么?
符号语言:
∵四边形ABCD是平行四边形 ∠A=90°
∴四边形ABCD是矩形
A
B
C
D
矩形既是轴对称图形,又是中心对称图形。
2、矩形有哪些性质
边:
角:
对角线:
对称性:
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分;
知识回顾
定理
符号语言
∵四边形ABCD是矩形
∴ ∠A=∠B=∠C=∠D =90°( )
矩形的四个角都是直角。
知识回顾
定理
∵四边形ABCD是矩形
∴ AC=BD( )
符号语言
矩形的对角线相等。
知识回顾
符号语言
直角三角形斜边上的中线等于斜边上的一半。
∵BE是R t△ABC斜边的中线,
∴ BE= AC( )
知识回顾
情景导入
现在仅有一根较长的绳子做工具,检查一下我们班级的门框(四边在同一平面上)是不是矩形,你有什么办法?
新知探究
你会判定一个平行四边形是矩形吗?
有一角是直角的平行四边形叫做矩形.
∠A=90°,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
符号语言
做一做
下面是一个平行四边形活动框架,拉动一对不相邻的顶点时,平行四边形的形状会发生变化。
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
(2)当两条对角线的长度相等时,平行四边形有什么特征?由此你能得到一个怎样的猜想?
对角线相等的平行四边形是矩形。
猜测与证明
已知:如图,在□ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:□ABCD是矩形.
证明:∵四边形ABCD是平行四边形
∴AB = DC AB∥ DC
又∵BC = CB,AC = DB,
∴△ABC≌△DCB
∴∠ABC = ∠DCB.
∵AB∥ DC
∴∠ABC + ∠DCB = 180°
∴ ∠ABC = 90°
∴ □ ABCD是矩形(矩形的定义)
对角线相等的平行四边形是矩形
定理
符号语言
∵四边形ABCD是平行四边形
又∵AC=BD
∴四边形ABCD是矩形( )
检验门框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则门框一定是矩形,你现在知道为什么了吗?
数学来源于生活
对角线相等的平行四边形是矩形
想一想
我们知道,矩形的四个角都是直角。反过来,一个四边形至少有几个角是直角时,这个四边形就是矩形了呢?请证明你的结论,并与同伴交流。
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
有三个角是直角的四边形是矩形。
猜测与证明
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
A
B
C
D
证明:∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°,
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形.
A
B
C
D
有三个角是直角的四边形是矩形。
定理
符号语言
∵在四边形ABCD中,∠A=∠B=∠C=90°
∴四边形ABCD是矩形( )
A
B
C
D
典例精析
例2:如图在□ABCD中,对角线AC和BD相较于点O,△ABO是等边三角形,AB=4.
求□ABCD的面积.
A
B
C
D
O
先独立思考,自己写下过程,小组之间交流对答案或者参考课本例2
1、已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.
求证:四边形ABCD是矩形.
当堂检测
2、已知:如图,菱形ABCD中,对角线AC 和BD 相较于点O,CM∥BD,DM∥AC.
求证:四边形OCMD是矩形.
当堂检测
当堂检测
3、在三角形ABC中,AD为BC边上的中线,延长AD至E,使DE=AD,连接BE,CE.
(1)试判断四边形ABEC的形状。
(2)当三角形ABC满足什么条件时,四边形ABEC是矩形?
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
