北师大版八年级上册1.3勾股定理的应用 课件 (共25张PPT)
文档属性
| 名称 | 北师大版八年级上册1.3勾股定理的应用 课件 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 649.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 16:32:00 | ||
图片预览




文档简介
(共25张PPT)
第一章 勾股定理
1.3勾股定理的应用
复习引入: (1分钟)
1.勾股定理:
直角三角形的两直角边为a、b,,斜边为 c,则有a2+b2=c2
如果一个三角形的三边a、b、c满足a2+b2=c2, 那么这个三角形是直角三角形.
2.直角三角形的判定方法:
3.两点之间 ,点到直线
线段最短
垂线段最短
学习目标: (1分钟)
1.熟练运用勾股定理和直角三角形的判定方法解决实际问题.
①利用勾股定理求线段长度
②利用直角三角形的判定方法来判断垂直关系
自学指导1:(6分钟)
1.自学课本P13做一做之前的内容,完成 :
①课本上的三个问题.
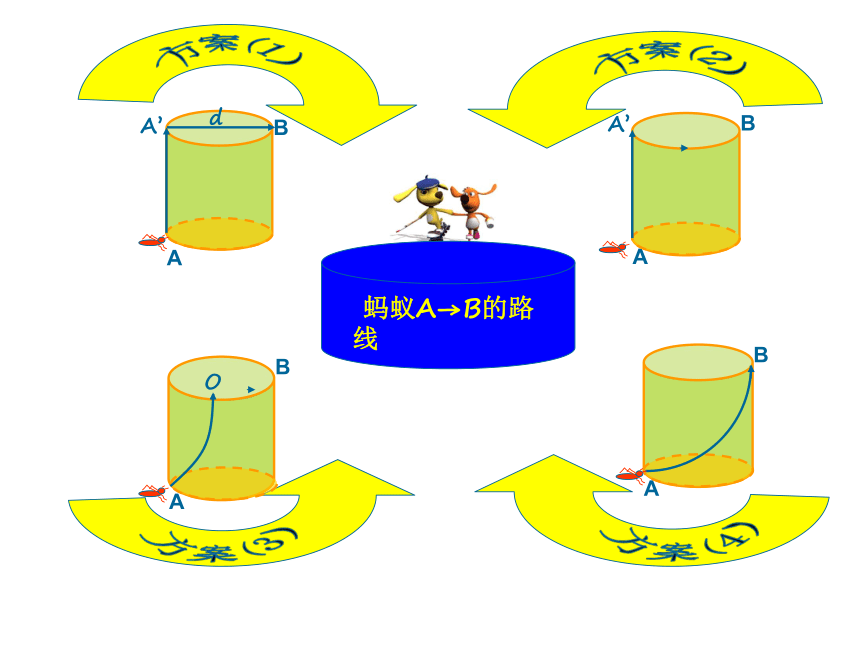
②如何求立体图形表面上任意两点之间的距离?
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
A
B
A’
B
A
A’
r
O
h
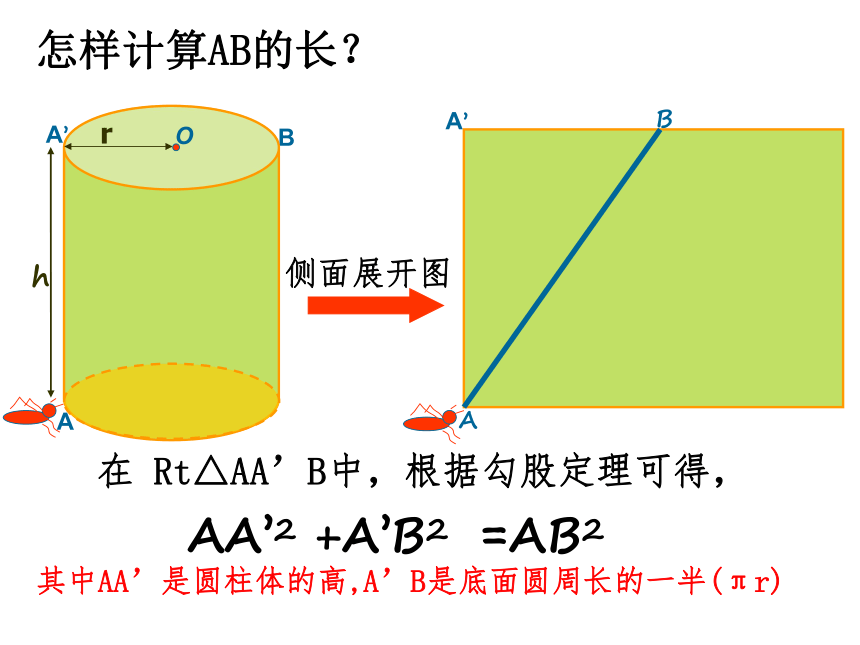
怎样计算AB的长?
在 Rt△AA’B中,根据勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
AA’2 +A’B2 =AB2
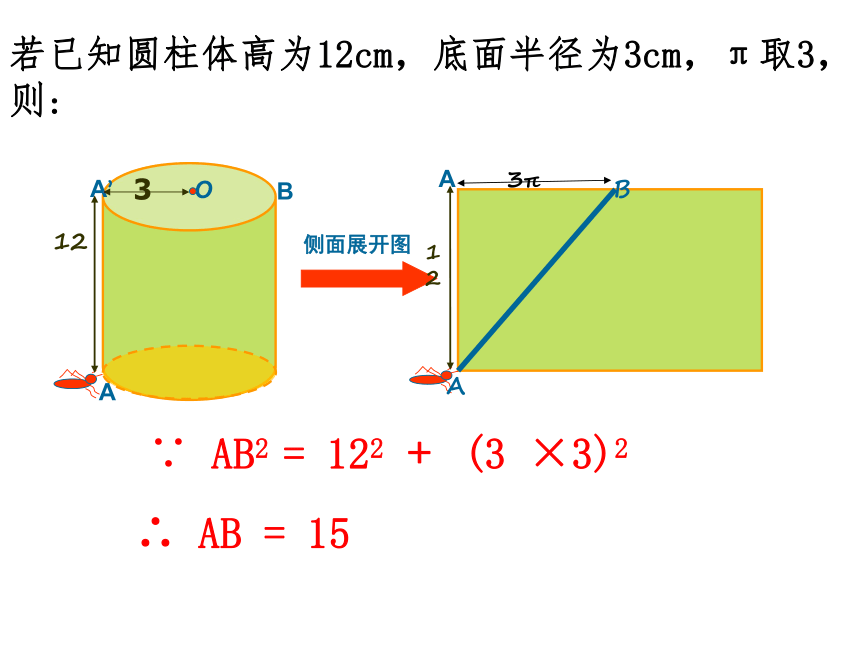
若已知圆柱体高为12cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
12
侧面展开图
12
3π
A
A
B
∵ AB2 = 122 ﹢ (3 ×3)2
∴ AB = 15
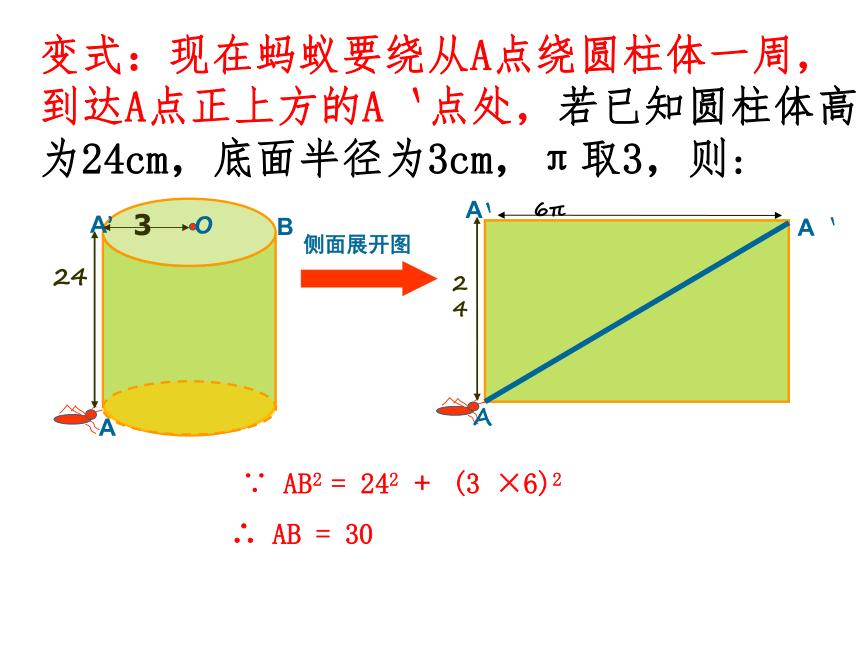
变式:现在蚂蚁要绕从A点绕圆柱体一周,
到达A点正上方的A`点处,若已知圆柱体高
为24cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
24
24
6π
A
A
A`
`
侧面展开图
∵ AB2 = 242 ﹢ (3 ×6)2
∴ AB = 30
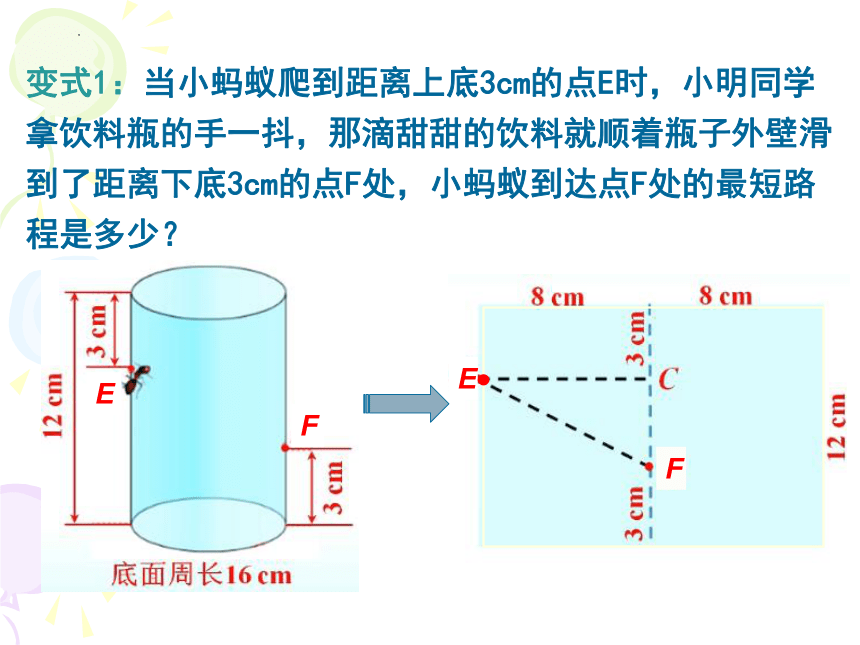
变式1:当小蚂蚁爬到距离上底3cm的点E时,小明同学拿饮料瓶的手一抖,那滴甜甜的饮料就顺着瓶子外壁滑到了距离下底3cm的点F处,小蚂蚁到达点F处的最短路程是多少?
E
F
E
F
E
F
E
F
解:把圆柱体的侧面展开如图,由题意得
在Rt ECF中,EF2=EC2+CF2=82+(12-3-3)2=100,
∴EF=10(cm).
即小蚂蚁到达点F处的最短路程是10cm
小结:
在遇到立体图形求最短路径问题中,第一步就是将立体图形展开成平面图形,找到对应点,在运用勾股定理进行求值
A
B
A
B
思考:如图正方体中如何求AB之间最短距离?
B2
思考:一个 无 盖的长方体形盒子的长、宽、高分别是8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短行程是多少?
B1
有
8
8
12
8
8
12
变式:一个 有 盖的长方体形盒子的长、宽、高分别是6cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的线路吗?
6
6
8
12
6
8
12
8
6
12
B1
B2
B3
AB2的路程最短
自学检测1 :(6分钟)
1.有一圆柱形油罐,底面周长12米,高5米,现从油罐底部A点环绕油罐建梯子,正好到A点的正上方B点,则梯子最短需多少米?
A
B
B
B′
A
A′
13m
2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎
么走最近?并求出最近距离.
∵AB2= 202 ﹢152
∴AB= 25
做一做
李叔叔想要检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30cm
边AB长是40cm,点B,D之间的距离是50cm
边AD垂直于边AB吗
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
自学指导2(2分钟)
2.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗 请你与同伴交流设计方案
1.课本P14习题1.4 T1,T2.
自学检测2 :(5分钟)
1. 在解一些求高度、宽度、长度、距离等的问题时,首
先要结合题意画出符合要求的直角三角形,也就是把
实际问题转化为数学问题,进而把要求的量看作直角
三角形的一条边,然后利用勾股定理进行求解.
2. 在日常生活中,判断一个角是否为直角时,除了用三
角板、量角器等测量角度的工具外,还可以通过测量
长度,结合计算来判断.
总结
自学指导3:(4分钟)
自学P13例题,并完成下题.
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(千米)
AC=1×5=5(千米)
在Rt△ABC中
∴BC=13(千米)
即甲乙两人相距13千米.
BC2=AC2+AB2=52+122=169=132
1.习题1.4,T3,T5
2.有一个高为1.5米,半径是1米的圆柱形 油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?
解:设伸入油桶中的长度为x米, 则最长时:
最短时:
∴最长是2.5+0.5=3(米)
答:这根铁棒的长应在2-3米之间.
∴最短是1.5+0.5=2(米)
自学检测3:(4分钟)
1.解决实际问题的方法是建立数学模型求解.
2.在寻求最短路径时,往往把空间问题平面化,利用勾股定理及其逆定理解决实际问题.
课堂小结(1分钟)
1.如图所示,一个梯子AB长为2.5米,顶端
靠在墙AC上,这时梯子下端B与墙角C的距离为1.5米,当梯子滑动后停在DE位置时,
这时BD=0.5米,求梯子顶端A下落了多少米.
A
B
E
D
C
当堂训练:(10分钟)
2.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?
B
食物
A
解:展开图如图所示:
A
B
C
扩展延伸
3
第一章 勾股定理
1.3勾股定理的应用
复习引入: (1分钟)
1.勾股定理:
直角三角形的两直角边为a、b,,斜边为 c,则有a2+b2=c2
如果一个三角形的三边a、b、c满足a2+b2=c2, 那么这个三角形是直角三角形.
2.直角三角形的判定方法:
3.两点之间 ,点到直线
线段最短
垂线段最短
学习目标: (1分钟)
1.熟练运用勾股定理和直角三角形的判定方法解决实际问题.
①利用勾股定理求线段长度
②利用直角三角形的判定方法来判断垂直关系
自学指导1:(6分钟)
1.自学课本P13做一做之前的内容,完成 :
①课本上的三个问题.
②如何求立体图形表面上任意两点之间的距离?
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
A
B
A’
B
A
A’
r
O
h
怎样计算AB的长?
在 Rt△AA’B中,根据勾股定理可得,
侧面展开图
其中AA’是圆柱体的高,A’B是底面圆周长的一半(πr)
AA’2 +A’B2 =AB2
若已知圆柱体高为12cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
12
侧面展开图
12
3π
A
A
B
∵ AB2 = 122 ﹢ (3 ×3)2
∴ AB = 15
变式:现在蚂蚁要绕从A点绕圆柱体一周,
到达A点正上方的A`点处,若已知圆柱体高
为24cm,底面半径为3cm,π取3,则:
B
A
A’
3
O
24
24
6π
A
A
A`
`
侧面展开图
∵ AB2 = 242 ﹢ (3 ×6)2
∴ AB = 30
变式1:当小蚂蚁爬到距离上底3cm的点E时,小明同学拿饮料瓶的手一抖,那滴甜甜的饮料就顺着瓶子外壁滑到了距离下底3cm的点F处,小蚂蚁到达点F处的最短路程是多少?
E
F
E
F
E
F
E
F
解:把圆柱体的侧面展开如图,由题意得
在Rt ECF中,EF2=EC2+CF2=82+(12-3-3)2=100,
∴EF=10(cm).
即小蚂蚁到达点F处的最短路程是10cm
小结:
在遇到立体图形求最短路径问题中,第一步就是将立体图形展开成平面图形,找到对应点,在运用勾股定理进行求值
A
B
A
B
思考:如图正方体中如何求AB之间最短距离?
B2
思考:一个 无 盖的长方体形盒子的长、宽、高分别是8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短行程是多少?
B1
有
8
8
12
8
8
12
变式:一个 有 盖的长方体形盒子的长、宽、高分别是6cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的线路吗?
6
6
8
12
6
8
12
8
6
12
B1
B2
B3
AB2的路程最短
自学检测1 :(6分钟)
1.有一圆柱形油罐,底面周长12米,高5米,现从油罐底部A点环绕油罐建梯子,正好到A点的正上方B点,则梯子最短需多少米?
A
B
B
B′
A
A′
13m
2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎
么走最近?并求出最近距离.
∵AB2= 202 ﹢152
∴AB= 25
做一做
李叔叔想要检测雕塑(如图)底座正面的边AD和边BC是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
(2)李叔叔量得边AD长是30cm
边AB长是40cm,点B,D之间的距离是50cm
边AD垂直于边AB吗
(3)小明随身只有一个长度为20cm的刻度尺,他能有办法检验边AD是否垂直于边AB吗?边BC与边AB呢?
自学指导2(2分钟)
2.右图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗 请你与同伴交流设计方案
1.课本P14习题1.4 T1,T2.
自学检测2 :(5分钟)
1. 在解一些求高度、宽度、长度、距离等的问题时,首
先要结合题意画出符合要求的直角三角形,也就是把
实际问题转化为数学问题,进而把要求的量看作直角
三角形的一条边,然后利用勾股定理进行求解.
2. 在日常生活中,判断一个角是否为直角时,除了用三
角板、量角器等测量角度的工具外,还可以通过测量
长度,结合计算来判断.
总结
自学指导3:(4分钟)
自学P13例题,并完成下题.
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走。上午10:00,甲、乙两人相距多远?
解:如图:已知A是甲、乙的出发点,10:00甲到达B点,乙到达C点.则:
AB=2×6=12(千米)
AC=1×5=5(千米)
在Rt△ABC中
∴BC=13(千米)
即甲乙两人相距13千米.
BC2=AC2+AB2=52+122=169=132
1.习题1.4,T3,T5
2.有一个高为1.5米,半径是1米的圆柱形 油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?
解:设伸入油桶中的长度为x米, 则最长时:
最短时:
∴最长是2.5+0.5=3(米)
答:这根铁棒的长应在2-3米之间.
∴最短是1.5+0.5=2(米)
自学检测3:(4分钟)
1.解决实际问题的方法是建立数学模型求解.
2.在寻求最短路径时,往往把空间问题平面化,利用勾股定理及其逆定理解决实际问题.
课堂小结(1分钟)
1.如图所示,一个梯子AB长为2.5米,顶端
靠在墙AC上,这时梯子下端B与墙角C的距离为1.5米,当梯子滑动后停在DE位置时,
这时BD=0.5米,求梯子顶端A下落了多少米.
A
B
E
D
C
当堂训练:(10分钟)
2.如图,在棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,且速度保持不变,问蚂蚁能否在20秒内从A爬到B?
B
食物
A
解:展开图如图所示:
A
B
C
扩展延伸
3
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
