北师大版八年级上册3.2.2平面直角坐标系课件(共24张PPT)
文档属性
| 名称 | 北师大版八年级上册3.2.2平面直角坐标系课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 253.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 16:45:32 | ||
图片预览







文档简介
(共24张PPT)
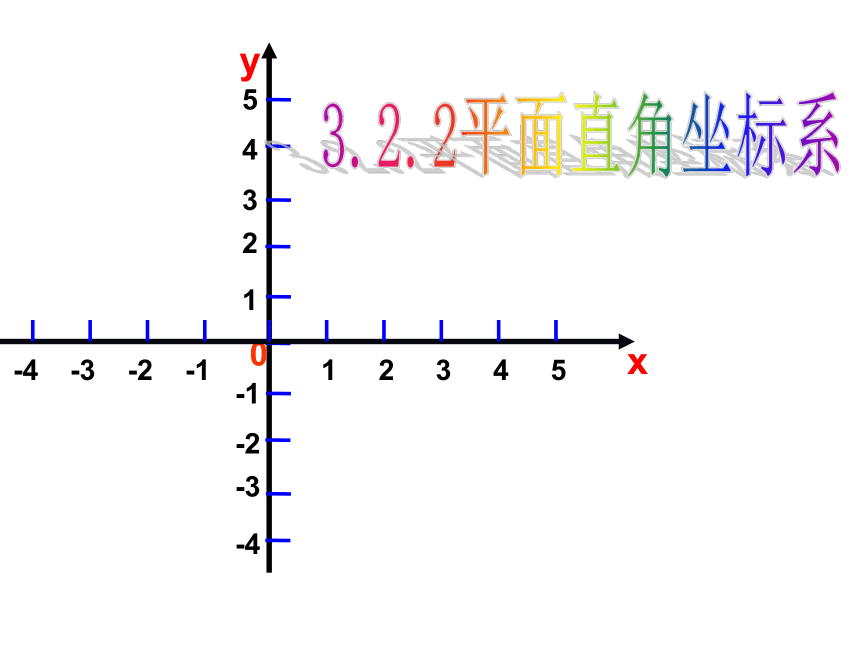
1、怎样建立平面直角坐标系?各个象限怎样分布?坐标轴上的点在哪个象限?
复习回顾(1分钟)
2、怎样确定平面内点的坐标?
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的 与 ,有序数对(a,b)叫做点P的 。
横坐标
纵坐标
坐标
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不在任何一个象限内。
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
3.2.2平面直角坐标系
学习目标:(1分钟)
1.能根据点的坐标在直角坐标系中找相对应的点的位置.
2.理解象限平分线上的点的特征.
3.关于x、y轴对称的点的坐标的特征.
1. x轴上的点有什么特征?
y轴上的点有什么特征?
坐标原点有什么特征?
学生自学,教师巡视(4分钟)
自学指导1(1分钟)
自学课本P62例2和P63的议一议,并完成
下列问题:
纵坐标为0
横坐标为0
坐标为(0,0)
2.平行于x 轴的直线上的点的坐标有什么特征?
平行于y 轴的直线上的点的坐标有什么特征?
平行于x轴的直线上的点的______ 相等。
平行于y轴的直线上的点的_______ 相等。
纵坐标
横坐标
引例:(P62页的例2)
在直角坐标系中描出下列各点,并将各组内
这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
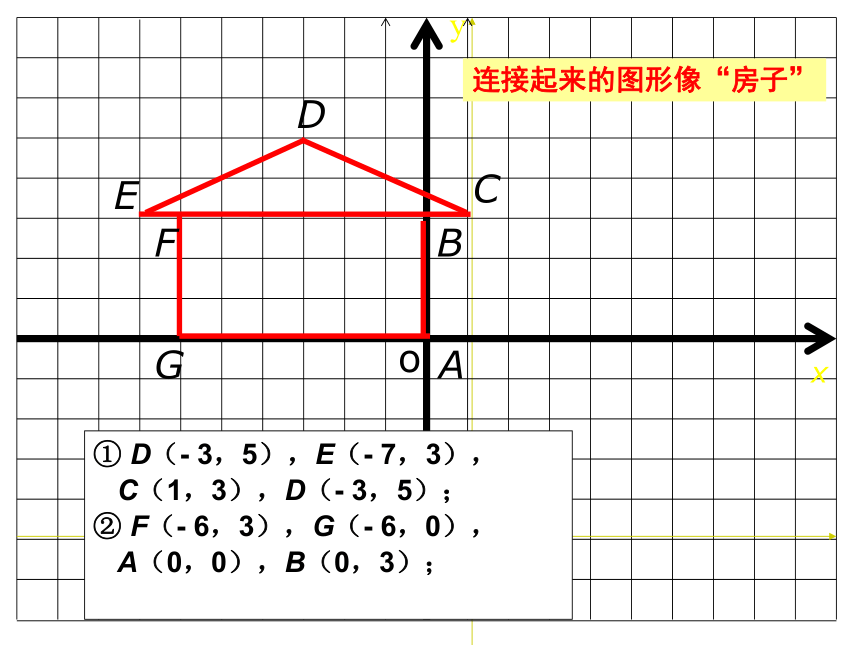
观察所描出的图形,它像什么?
自学指导1:(5分钟)
-1
y
x
A
B
C
D
G
E
F
o
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
连接起来的图形像“房子”
-1
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
B
G
o
A
C
D
E
F
线段 AG 上的点都在 x 轴上,它们的纵坐标等于 0
线段 AB 上的点都在 y 轴上,它们的横坐标等于 0
(2)线段 EC 与 x 轴有什么位置关系?点 E 和点 C 的坐标有什么特点?线段 EC 上其他点的坐标呢?
线段 EC 平行于 x 轴,点 E 和点 C 的纵坐标相同.
线段 EC 上其他点的纵坐标相同,都是 3.
-1
(3)点 F 和点G 的横坐标有什么共同特点,线段 FG 与 y 轴有怎样的位置关系?
B
G
o
A
C
D
E
F
点 F 和点G 的横坐标相同,线段 FG 与 y 轴平行
1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。
归纳概括
纵坐标等于 0
横坐标等于 0
纵坐标相同
横坐标相同
1.若点P(-6,a-3)在x轴上,则a= ;
若点P(a2 -1,a+3)在y轴上,则a=_______;
2.已知点A(-5,3),点B(a,b),
若AB平行于x轴,则b= ;
若AB平行于y轴,则a= ;
若AB平行于x轴,且B点在y轴上,则B点的坐标________.
若AB平行于y轴,且A点距离B点两个单位长度,则B点的 坐标为________________.
3
1或-1
3
-5
(0,3)
(-5,5)或(-5,1)
自学检测1:(5分钟)
3.实数 x,y满足 (x-1)2+ = 0,则点 P( x,y)在( ).
(A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B
4. 如果同一直角坐标平面内两个点的横坐标相同,那么过这两点的直线( ) .
(A)平行于 x轴 (B)平行于 y轴
(C)经过原点 (D)以上都不对
D
6.完成课本
5.已知点A(a,4)与点B(-2,b),若直线
AB∥x轴,则a、b满足的条件是 ,
若AB∥y轴,则a、b满足的条件是 。
b=4且a≠-2
a=-2且b≠4
-1
o
y
x
-2
-6
2
6
2
6
7.在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来。观察它是什么形状的图形?
A(0,5),B(-4,0),C(-9,4)。
等腰直角三角形
-9
4
A
B
C
AB2=52+42=41
BC2=52+42=41
AC2=92+12=82
AB=BC
AB2+BC2=AC2
5
-1
0
1
3
2
3
2
1
5
4
5
4
-2
-4
-4
-2
y
x
-3
-3
-1
N
M
D
E
F
G
H
A
B
C
Q
P
讨论、更正、点拔(4分钟):
(-2,6)
(3,6)
(6,3)
(3,5)
(-5,-2)
(-5,3)
(6,-2)
(0,6)
(-5,0)
(6,0)
(-2,-5)
(0,-5)
1.数轴上的点横、 纵坐标有什么特征?
2.与数轴平行的直线上的点的坐标有什么特征?
x轴上的点的纵坐标
为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
当点在同一条平行于x轴的直线上时,各个点的纵坐标相同
当点在同一条平行于y轴的直线上时,各个点的横坐标相同;
1、各象限的角平分线上的点的坐标有什么关系?
2、点的坐标与距离的关系是什么?
自学指导2:(5分钟)
-1
y
x
A
B
C
G
o
各象限上的角平分线上
的点的关系
(2,2)
(3,3)
(-3,-3)
(-4,-4)
点M(x,y)在一三象限的角平分线上满足x=y.即横坐标与纵坐标相等 如(3,3)(-4,-4)
(-3,3)
(2,-2)
(3,-3)
点M(x,y)在二四象限的角平分线上满足x+y=0.即横坐标与纵坐标互为相反数
如(-4,4)(2,-2)
y
45°
1、坐标点P(a,b)到X轴的距离为 ,到
Y轴的距离为 , 到原点的距离为 。
2、若P点的坐标到X轴、Y轴的距离分别为a,b,则点P的坐标为______________________________________
( b,a),(b,-a),(-b,a)或(-b,-a)
.
∟
∟
a
b
o
x
y
p
(a, b)
a
b
自学检测2:(5分钟)
1.若点A(5-a,a-3)在第一、三象限的角平分线上,
则a= ,点A的坐标为 ..点
2.若点A(a2-3,-1)在第二、四象限的角平分线上,
则a= ,点A的坐标为 .
3.已知线段AB=3,AB∥x轴,若A点坐标(-1,2),
则B点坐标是 .
4.已知点 在y的负半轴则a为_____.
(1,1)
4
(1,-1)
(2,2)或(-4,2)
a=-2
(-2,3)
(-4,-1)
(2,-2)
(4,3)
3
1
2
-2
-1
0
1
2
3
4
-4
-3
-2
-1
·
Q
·
P
·
M
·
N
x
y
到X 轴的距离是: 到X 轴的距离是:
到Y 轴的距离是: 到Y 轴的距离是:
到原点的距离是: 到原点的距离是:
点P
点Q
3
4
5
2
3
请说出P,Q,M,N四个点的坐标并填空.
变式1:点Q在第一象限且离x轴、y轴的距离分别是2、3,试写出点Q的坐标.
-1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
解: 点Q的坐标是(3,2)
变式1:点Q在第二象限且离x轴、y轴的距离分别是2、3,试写出点Q的坐标.
-1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
解: 点Q的坐标是(-3,2)
Q在第三象限
Q在第四象限
(-3,-2)
(3,-2)
变式:点Q离x轴、y轴的距离分别是2、3,试写出点Q的坐标.
-1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
解: 点Q的坐标是(3,2)、
(-3,2)、(-3,-2)、(3,-2)
若P点到X轴、Y轴的距离
分别为a,b,则点P的坐标为:
( b,a),(b,-a),
(-b,a)或(-b,-a)
当堂训练:(8分钟)
1.如果点 在第一象限,那么点F 在( ).
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.矩形ABCD中,三点的坐标分别是 (0,0)(5,0)(5,3),则第四个点D点的坐标是( ).
C
C
3.点A在坐标轴上,且距离原点4个单位长度,则A点的坐标是 .
4.在平面直角坐标系内,已知点P ( a , b ), 且
a b < 0 , 则点P的位置在 .
(4,0)或(0,4)或(-4,0)或(0,-4)
第二象限或者第四象限
5.点A(3,4)到x轴的距离是____,到y轴的距离
是_______,到原点的距离是____.
6.点D(3,0)和点E(0,4)之间的距离为_____.
7.直角坐标系中,点P(x,y)在第二象限,且P到x 轴、y轴距离分别为3,7,则点P坐标为( ).
B
5
3
4
5
8.点 A 在第一象限,当 m =____时,点 A
(m + 1,3m - 5)到 x轴的距离是它到 y轴距离的两倍 .
7
x
y
O
A
B
9、如图,点A在 x轴的负半轴上,AB垂直于x轴,OA=3 ,OB=5 ,求点B的坐标。
解:如图,在Rt△AOB中
由勾股定理得,
AB2=52-32=42
∴AB=4 ∴B(-3,4)
10.点(m,-1)和点(2,n)关于x轴对称,则mn等于( ) .
A.- 2 B.2 C.1 D.- 1
A
1、怎样建立平面直角坐标系?各个象限怎样分布?坐标轴上的点在哪个象限?
复习回顾(1分钟)
2、怎样确定平面内点的坐标?
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的 与 ,有序数对(a,b)叫做点P的 。
横坐标
纵坐标
坐标
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不在任何一个象限内。
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
3.2.2平面直角坐标系
学习目标:(1分钟)
1.能根据点的坐标在直角坐标系中找相对应的点的位置.
2.理解象限平分线上的点的特征.
3.关于x、y轴对称的点的坐标的特征.
1. x轴上的点有什么特征?
y轴上的点有什么特征?
坐标原点有什么特征?
学生自学,教师巡视(4分钟)
自学指导1(1分钟)
自学课本P62例2和P63的议一议,并完成
下列问题:
纵坐标为0
横坐标为0
坐标为(0,0)
2.平行于x 轴的直线上的点的坐标有什么特征?
平行于y 轴的直线上的点的坐标有什么特征?
平行于x轴的直线上的点的______ 相等。
平行于y轴的直线上的点的_______ 相等。
纵坐标
横坐标
引例:(P62页的例2)
在直角坐标系中描出下列各点,并将各组内
这些点依次用线段连接起来(如下图 ).
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
观察所描出的图形,它像什么?
自学指导1:(5分钟)
-1
y
x
A
B
C
D
G
E
F
o
① D(- 3,5),E(- 7,3),
C(1,3),D(- 3,5);
② F(- 6,3),G(- 6,0),
A(0,0),B(0,3);
连接起来的图形像“房子”
-1
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
B
G
o
A
C
D
E
F
线段 AG 上的点都在 x 轴上,它们的纵坐标等于 0
线段 AB 上的点都在 y 轴上,它们的横坐标等于 0
(2)线段 EC 与 x 轴有什么位置关系?点 E 和点 C 的坐标有什么特点?线段 EC 上其他点的坐标呢?
线段 EC 平行于 x 轴,点 E 和点 C 的纵坐标相同.
线段 EC 上其他点的纵坐标相同,都是 3.
-1
(3)点 F 和点G 的横坐标有什么共同特点,线段 FG 与 y 轴有怎样的位置关系?
B
G
o
A
C
D
E
F
点 F 和点G 的横坐标相同,线段 FG 与 y 轴平行
1.位于x轴上的点的坐标的特征是: ;
位于y轴上的点的坐标的特征是: 。
2.与x轴平行的直线上点的坐标的特征
是: ;
与y轴平行的直线上点的坐标的特征
是: 。
归纳概括
纵坐标等于 0
横坐标等于 0
纵坐标相同
横坐标相同
1.若点P(-6,a-3)在x轴上,则a= ;
若点P(a2 -1,a+3)在y轴上,则a=_______;
2.已知点A(-5,3),点B(a,b),
若AB平行于x轴,则b= ;
若AB平行于y轴,则a= ;
若AB平行于x轴,且B点在y轴上,则B点的坐标________.
若AB平行于y轴,且A点距离B点两个单位长度,则B点的 坐标为________________.
3
1或-1
3
-5
(0,3)
(-5,5)或(-5,1)
自学检测1:(5分钟)
3.实数 x,y满足 (x-1)2+ = 0,则点 P( x,y)在( ).
(A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置
B
4. 如果同一直角坐标平面内两个点的横坐标相同,那么过这两点的直线( ) .
(A)平行于 x轴 (B)平行于 y轴
(C)经过原点 (D)以上都不对
D
6.完成课本
5.已知点A(a,4)与点B(-2,b),若直线
AB∥x轴,则a、b满足的条件是 ,
若AB∥y轴,则a、b满足的条件是 。
b=4且a≠-2
a=-2且b≠4
-1
o
y
x
-2
-6
2
6
2
6
7.在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来。观察它是什么形状的图形?
A(0,5),B(-4,0),C(-9,4)。
等腰直角三角形
-9
4
A
B
C
AB2=52+42=41
BC2=52+42=41
AC2=92+12=82
AB=BC
AB2+BC2=AC2
5
-1
0
1
3
2
3
2
1
5
4
5
4
-2
-4
-4
-2
y
x
-3
-3
-1
N
M
D
E
F
G
H
A
B
C
Q
P
讨论、更正、点拔(4分钟):
(-2,6)
(3,6)
(6,3)
(3,5)
(-5,-2)
(-5,3)
(6,-2)
(0,6)
(-5,0)
(6,0)
(-2,-5)
(0,-5)
1.数轴上的点横、 纵坐标有什么特征?
2.与数轴平行的直线上的点的坐标有什么特征?
x轴上的点的纵坐标
为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
当点在同一条平行于x轴的直线上时,各个点的纵坐标相同
当点在同一条平行于y轴的直线上时,各个点的横坐标相同;
1、各象限的角平分线上的点的坐标有什么关系?
2、点的坐标与距离的关系是什么?
自学指导2:(5分钟)
-1
y
x
A
B
C
G
o
各象限上的角平分线上
的点的关系
(2,2)
(3,3)
(-3,-3)
(-4,-4)
点M(x,y)在一三象限的角平分线上满足x=y.即横坐标与纵坐标相等 如(3,3)(-4,-4)
(-3,3)
(2,-2)
(3,-3)
点M(x,y)在二四象限的角平分线上满足x+y=0.即横坐标与纵坐标互为相反数
如(-4,4)(2,-2)
y
45°
1、坐标点P(a,b)到X轴的距离为 ,到
Y轴的距离为 , 到原点的距离为 。
2、若P点的坐标到X轴、Y轴的距离分别为a,b,则点P的坐标为______________________________________
( b,a),(b,-a),(-b,a)或(-b,-a)
.
∟
∟
a
b
o
x
y
p
(a, b)
a
b
自学检测2:(5分钟)
1.若点A(5-a,a-3)在第一、三象限的角平分线上,
则a= ,点A的坐标为 ..点
2.若点A(a2-3,-1)在第二、四象限的角平分线上,
则a= ,点A的坐标为 .
3.已知线段AB=3,AB∥x轴,若A点坐标(-1,2),
则B点坐标是 .
4.已知点 在y的负半轴则a为_____.
(1,1)
4
(1,-1)
(2,2)或(-4,2)
a=-2
(-2,3)
(-4,-1)
(2,-2)
(4,3)
3
1
2
-2
-1
0
1
2
3
4
-4
-3
-2
-1
·
Q
·
P
·
M
·
N
x
y
到X 轴的距离是: 到X 轴的距离是:
到Y 轴的距离是: 到Y 轴的距离是:
到原点的距离是: 到原点的距离是:
点P
点Q
3
4
5
2
3
请说出P,Q,M,N四个点的坐标并填空.
变式1:点Q在第一象限且离x轴、y轴的距离分别是2、3,试写出点Q的坐标.
-1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
解: 点Q的坐标是(3,2)
变式1:点Q在第二象限且离x轴、y轴的距离分别是2、3,试写出点Q的坐标.
-1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
解: 点Q的坐标是(-3,2)
Q在第三象限
Q在第四象限
(-3,-2)
(3,-2)
变式:点Q离x轴、y轴的距离分别是2、3,试写出点Q的坐标.
-1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
解: 点Q的坐标是(3,2)、
(-3,2)、(-3,-2)、(3,-2)
若P点到X轴、Y轴的距离
分别为a,b,则点P的坐标为:
( b,a),(b,-a),
(-b,a)或(-b,-a)
当堂训练:(8分钟)
1.如果点 在第一象限,那么点F 在( ).
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.矩形ABCD中,三点的坐标分别是 (0,0)(5,0)(5,3),则第四个点D点的坐标是( ).
C
C
3.点A在坐标轴上,且距离原点4个单位长度,则A点的坐标是 .
4.在平面直角坐标系内,已知点P ( a , b ), 且
a b < 0 , 则点P的位置在 .
(4,0)或(0,4)或(-4,0)或(0,-4)
第二象限或者第四象限
5.点A(3,4)到x轴的距离是____,到y轴的距离
是_______,到原点的距离是____.
6.点D(3,0)和点E(0,4)之间的距离为_____.
7.直角坐标系中,点P(x,y)在第二象限,且P到x 轴、y轴距离分别为3,7,则点P坐标为( ).
B
5
3
4
5
8.点 A 在第一象限,当 m =____时,点 A
(m + 1,3m - 5)到 x轴的距离是它到 y轴距离的两倍 .
7
x
y
O
A
B
9、如图,点A在 x轴的负半轴上,AB垂直于x轴,OA=3 ,OB=5 ,求点B的坐标。
解:如图,在Rt△AOB中
由勾股定理得,
AB2=52-32=42
∴AB=4 ∴B(-3,4)
10.点(m,-1)和点(2,n)关于x轴对称,则mn等于( ) .
A.- 2 B.2 C.1 D.- 1
A
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
