北师大版八年级数学上册 1.1 探索勾股定理 习题1(word版含答案)
文档属性
| 名称 | 北师大版八年级数学上册 1.1 探索勾股定理 习题1(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览

文档简介
1.1 《探索勾股定理》 习题1
一、填空题
1.在Rt△ABC中,∠C=90°.
(1)已知a:b=3:4,c=10,则a= ,b= ;
(2)已知a=6,b=8,则斜边c上的高h= .
2.在Rt△ABC中,斜边AB=3,则AB2+BC2+CA2= .
3.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
4.在Rt△ABC中,∠C=90°,AB=25cm,AC=15cm,CH⊥AB垂足为H,CH= .
5.如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,则BE的长为 .
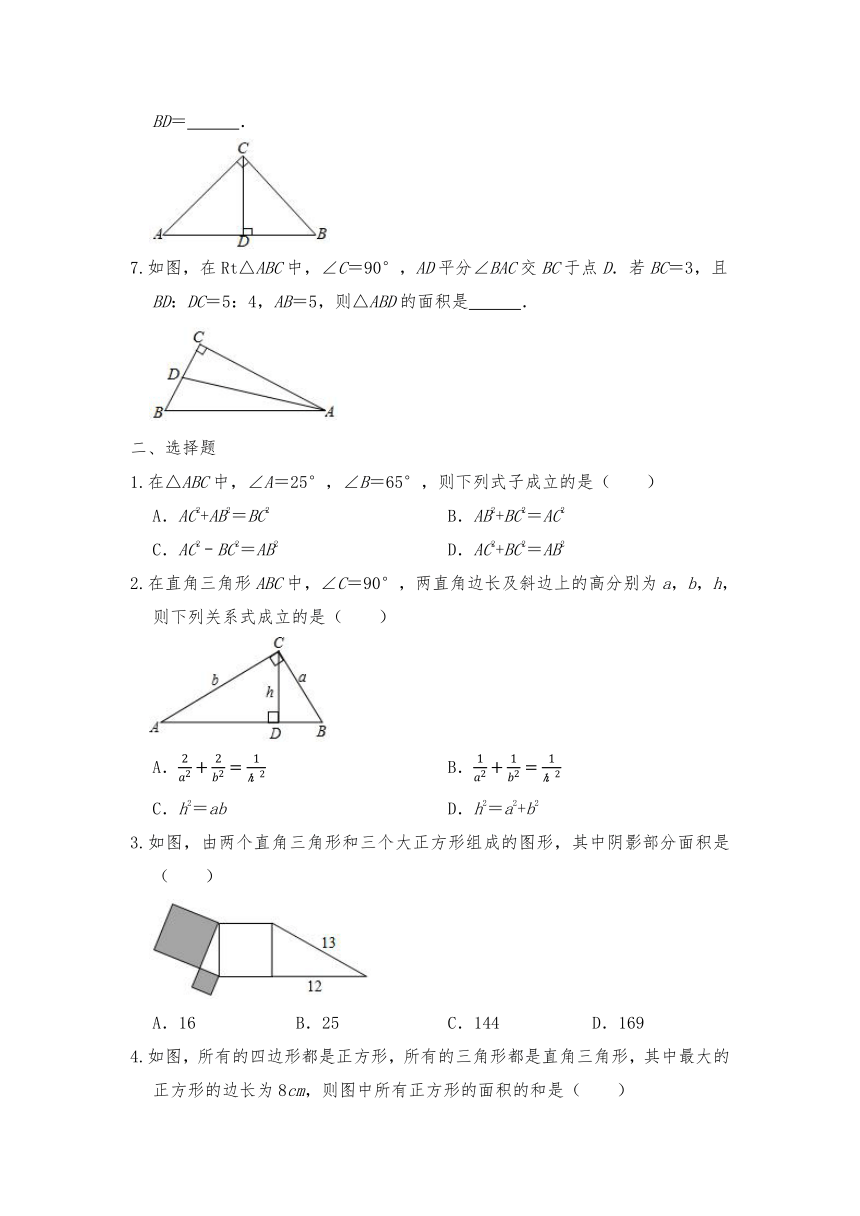
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=6,AD=3,那么BD= .
7.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BC=3,且BD:DC=5:4,AB=5,则△ABD的面积是 .
二、选择题
1.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+AB2=BC2 B.AB2+BC2=AC2
C.AC2﹣BC2=AB2 D.AC2+BC2=AB2
2.在直角三角形ABC中,∠C=90°,两直角边长及斜边上的高分别为a,b,h,则下列关系式成立的是( )
A. B.
C.h2=ab D.h2=a2+b2
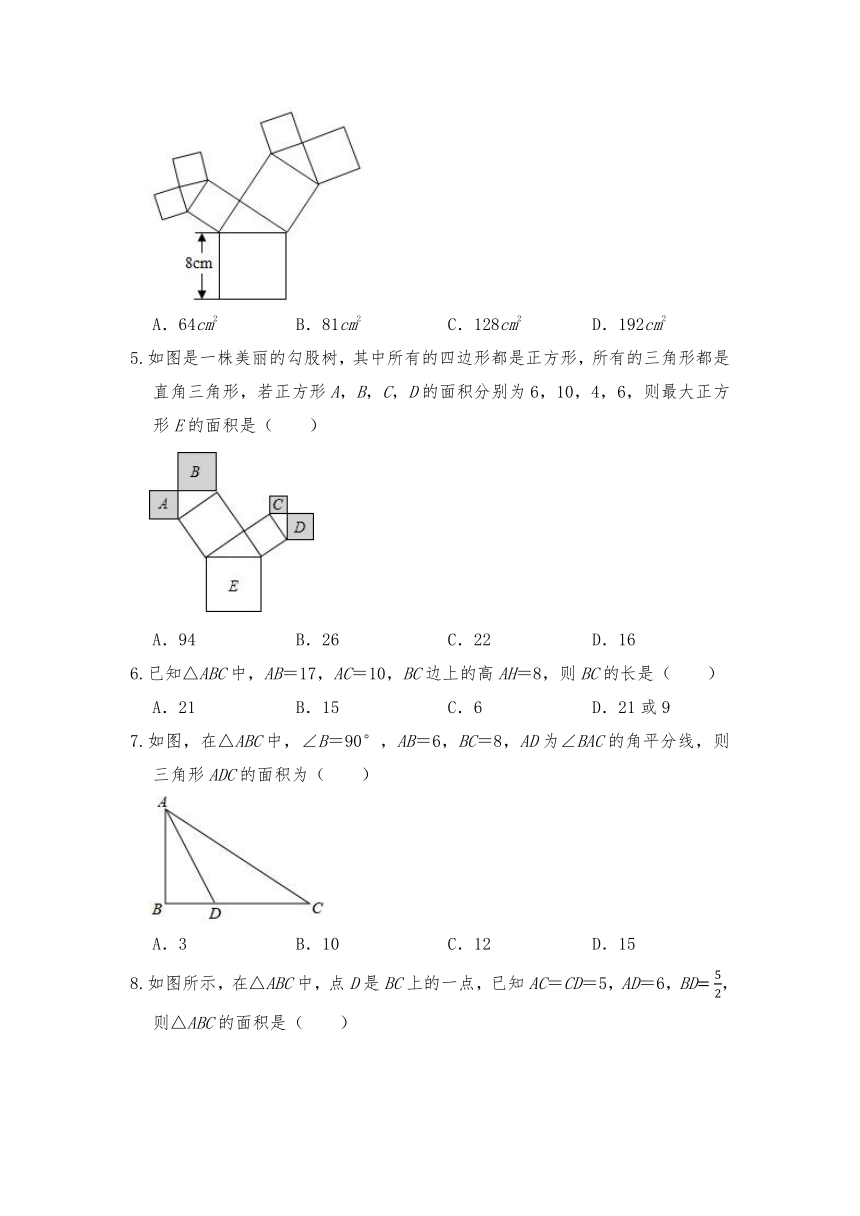
3.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A.16 B.25 C.144 D.169
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8cm,则图中所有正方形的面积的和是( )
A.64cm2 B.81cm2 C.128cm2 D.192cm2
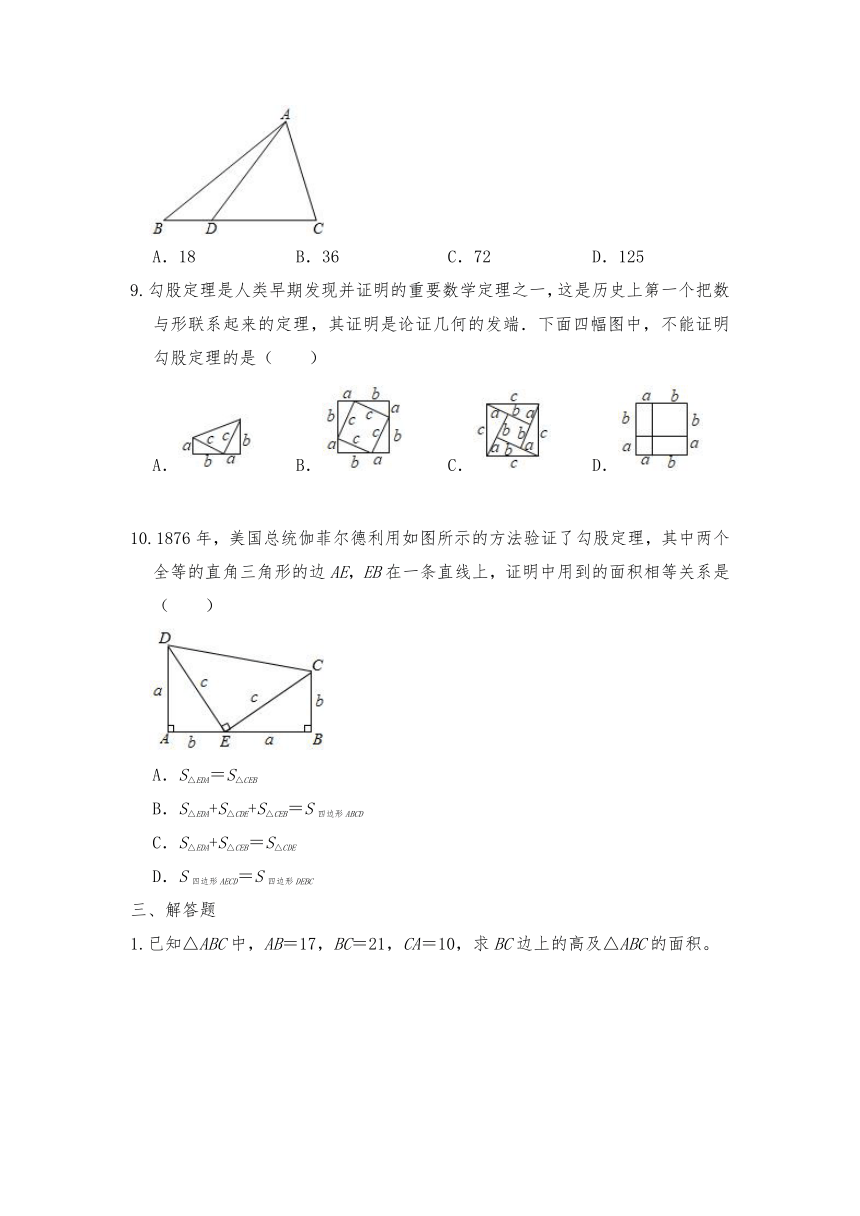
5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为6,10,4,6,则最大正方形E的面积是( )
A.94 B.26 C.22 D.16
6.已知△ABC中,AB=17,AC=10,BC边上的高AH=8,则BC的长是( )
A.21 B.15 C.6 D.21或9
7.如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的角平分线,则三角形ADC的面积为( )
A.3 B.10 C.12 D.15
8.如图所示,在△ABC中,点D是BC上的一点,已知AC=CD=5,AD=6,BD,则△ABC的面积是( )
A.18 B.36 C.72 D.125
9.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
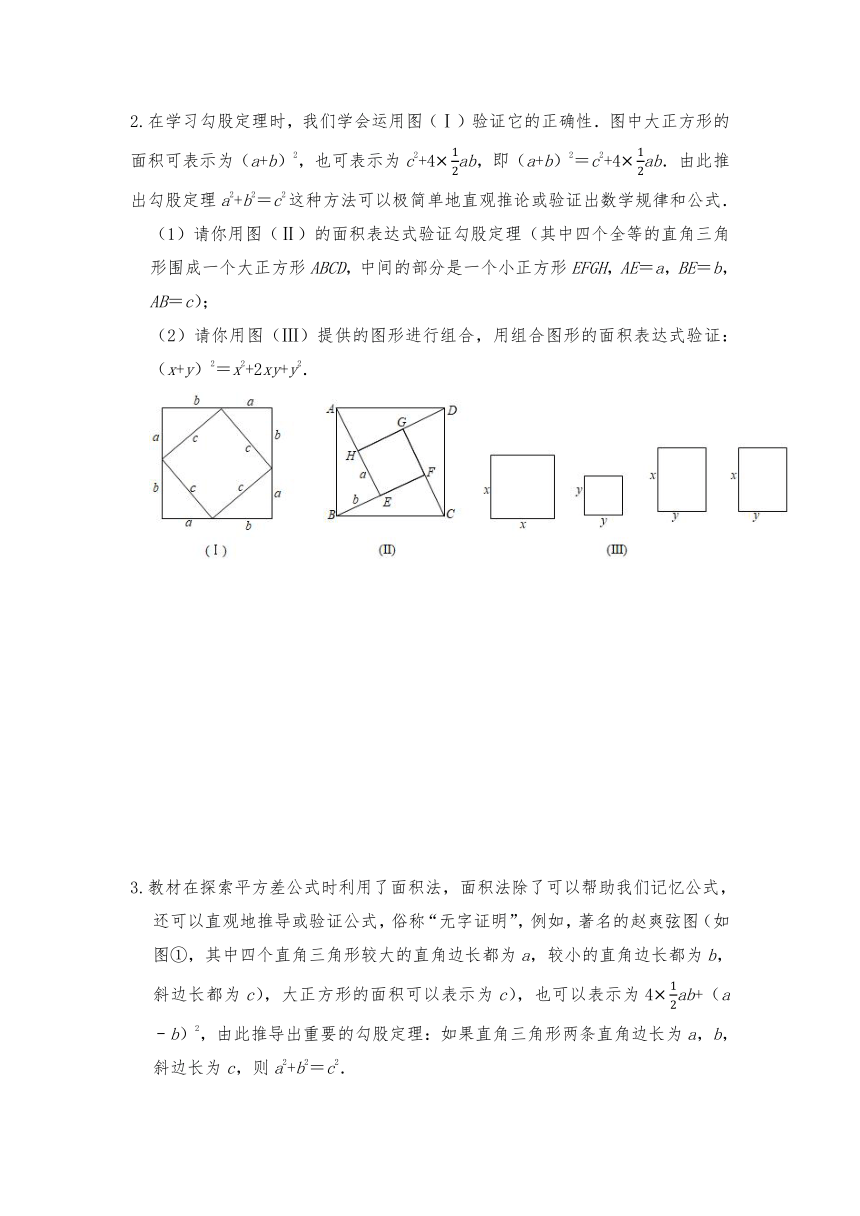
10.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE
D.S四边形AECD=S四边形DEBC
三、解答题
1.已知△ABC中,AB=17,BC=21,CA=10,求BC边上的高及△ABC的面积。
2.在学习勾股定理时,我们学会运用图(Ⅰ)验证它的正确性.图中大正方形的面积可表示为(a+b)2,也可表示为c2+4ab,即(a+b)2=c2+4ab.由此推出勾股定理a2+b2=c2这种方法可以极简单地直观推论或验证出数学规律和公式.
(1)请你用图(Ⅱ)的面积表达式验证勾股定理(其中四个全等的直角三角形围成一个大正方形ABCD,中间的部分是一个小正方形EFGH,AE=a,BE=b,AB=c);
(2)请你用图(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+y)2=x2+2xy+y2.
3.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2,画在如图4的网格中,并标出字母a,b所表示的线段.
4.如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.
5.如图,木工师傅将一根长2.5米的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7米,如果梯子的顶端A沿墙下滑0.4米到点A′时,梯足将外移多少米?
6.如图是某“飞越丛林”俱乐部新近打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形CDEF为一木质平台的主视图.小敏经过现场测量得知:CD=1米,AD=15米,于是小敏大胆猜想立柱AB段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱AB段的正确长度.
7.为了积极宣传防疫,南川区政府采用了移动车进行广播,如图,小明家在南大街这条笔直的公路MN的一侧点A处,小明家到公路MN的距离为600米,假使广播车P周围1000米以内能听到广播宣传,广播车P以250米/分的速度在公路MN上沿PN方向行驶时,若小明此时在家,他是否能听到?若能,请求出他总共能听到多长时间的广播?
答案
一、填空题
1.6,8;4.8. 2.18 3.9π.4.12cm. 5.. 6.9. 7..
二、选择题
1.D.2.B.3.B.4.D.5.B.6.D.7.D.8.A.9.D.10.B.
三、解答题
1.解:作AD⊥BC于D,
设CD=x,则BD=21﹣x,
在Rt△ACD中,AD2=AC2﹣CD2,
在Rt△ABD中,AD2=AB2﹣BD2,
∴AC2﹣CD2=AB2﹣BD2,即102﹣x2=172﹣(21﹣x)2,
解得,x=6,即CD=6,
则AD8,
△ABC的面积BC×AD21×8=84.
2.解:(1)大正方形的面积为:c2,中间小正方形面积为:(b﹣a)2;
四个直角三角形面积和为:4ab;
由图形关系可知:大正方形面积=小正方形面积+四直角三角形面积,
即有:c2=(b﹣a)2+4ab=b2﹣2ab+a2+2ab=a2+b2;
(2)如图示:
大正方形边长为(x+y)所以面积为:(x+y)2,它的面积也等于两个边长分别为x,y和两个长为x宽为y的矩形面积之和,即x2+2xy+y2
所以有:(x+y)2=x2+2xy+y2成立;
3.解:(1)梯形ABCD的面积为,
也可以表示为,∴,
即a2+b2=c2;
(2)在Rt△ABD中,AD2=AB2﹣BD2=42﹣x2=16﹣x2;
在Rt△ADC中,AD2=AC2﹣DC2=52﹣(6﹣x)2=﹣11+12x﹣x2;
所以16﹣x2=﹣11+12x﹣x2,
解得;
(3)如图,
由此可得(a+b)(a+2b)=a2+3ab+2b2.
4.解:依题意得AC=2,AE=3,
设原标杆的高为x,
∵∠A=90°,
∴由题中条件可得AB2+AC2=BC2,即AB2+22=(x﹣AB)2,
整理,得x2﹣2ABx=4,
同理,得(AB﹣0.5)2+32=(x﹣AB+0.5)2,
整理,得x2﹣2ABx+x=9,
解得x=5.
∴原来标杆的高度为5米.
5.解:在直角△ABO中,AB为斜边,已知AB=2.5米,BO=0.7米,
则根据勾股定理求得AO2.4(米),
∵A点下移0.4米,
∴A′O=2米,
在Rt△A′OB′中,已知A′B′=2.5米,A′O=2米,
则根据勾股定理B′O1.5(米),
∴BB′=OB′﹣BO=1.5﹣0.7=0.8(米),
所以梯子向外平移0.8米.
6.解:不正确;
理由:如答图,延长FC交AB于点G,
则CG⊥AB,AG=CD=1米,GC=AD=15米,
设BG=x米,则BC=(26﹣1﹣x)米,
在Rt△BGC中,
∵BG2+CG2=CB2,
∴x2+152=(26﹣1﹣x)2,
解得x=8,
∴BA=BG+GA=8+1=9(米),
∴小敏的猜想错误,立柱AB段的正确长度长为9米.
7.解:小明能听到宣传,
理由:∵村庄A到公路MN的距离为600米<1000米,
∴小明能听到宣传;
如图:假设当宣讲车行驶到P点开始小明听到广播,行驶到Q点小明听不到广播,
则AP=AQ=1000米,AB=600米,
∴BP=BQ800(米),∴PQ=1600米,
∴小明听到广播的时间为:1600÷250=6.4(分钟),
∴他总共能听到6.4分钟的广播.
一、填空题
1.在Rt△ABC中,∠C=90°.
(1)已知a:b=3:4,c=10,则a= ,b= ;
(2)已知a=6,b=8,则斜边c上的高h= .
2.在Rt△ABC中,斜边AB=3,则AB2+BC2+CA2= .
3.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
4.在Rt△ABC中,∠C=90°,AB=25cm,AC=15cm,CH⊥AB垂足为H,CH= .
5.如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,则BE的长为 .
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,如果AC=6,AD=3,那么BD= .
7.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BC=3,且BD:DC=5:4,AB=5,则△ABD的面积是 .
二、选择题
1.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+AB2=BC2 B.AB2+BC2=AC2
C.AC2﹣BC2=AB2 D.AC2+BC2=AB2
2.在直角三角形ABC中,∠C=90°,两直角边长及斜边上的高分别为a,b,h,则下列关系式成立的是( )
A. B.
C.h2=ab D.h2=a2+b2
3.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A.16 B.25 C.144 D.169
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8cm,则图中所有正方形的面积的和是( )
A.64cm2 B.81cm2 C.128cm2 D.192cm2
5.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积分别为6,10,4,6,则最大正方形E的面积是( )
A.94 B.26 C.22 D.16
6.已知△ABC中,AB=17,AC=10,BC边上的高AH=8,则BC的长是( )
A.21 B.15 C.6 D.21或9
7.如图,在△ABC中,∠B=90°,AB=6,BC=8,AD为∠BAC的角平分线,则三角形ADC的面积为( )
A.3 B.10 C.12 D.15
8.如图所示,在△ABC中,点D是BC上的一点,已知AC=CD=5,AD=6,BD,则△ABC的面积是( )
A.18 B.36 C.72 D.125
9.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
10.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB
B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE
D.S四边形AECD=S四边形DEBC
三、解答题
1.已知△ABC中,AB=17,BC=21,CA=10,求BC边上的高及△ABC的面积。
2.在学习勾股定理时,我们学会运用图(Ⅰ)验证它的正确性.图中大正方形的面积可表示为(a+b)2,也可表示为c2+4ab,即(a+b)2=c2+4ab.由此推出勾股定理a2+b2=c2这种方法可以极简单地直观推论或验证出数学规律和公式.
(1)请你用图(Ⅱ)的面积表达式验证勾股定理(其中四个全等的直角三角形围成一个大正方形ABCD,中间的部分是一个小正方形EFGH,AE=a,BE=b,AB=c);
(2)请你用图(Ⅲ)提供的图形进行组合,用组合图形的面积表达式验证:(x+y)2=x2+2xy+y2.
3.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2,画在如图4的网格中,并标出字母a,b所表示的线段.
4.如图,有一直立标杆,它的上部被风从B处吹折,杆顶C着地,离杆脚2m,修好后又被风吹折,因新断处D比前一次低0.5m,故杆顶E着地比前次远1m,求原标杆的高度.
5.如图,木工师傅将一根长2.5米的梯子(AB),斜靠在与地面(OM)垂直的墙(ON)上,这时梯足B到墙底端O的距离是0.7米,如果梯子的顶端A沿墙下滑0.4米到点A′时,梯足将外移多少米?
6.如图是某“飞越丛林”俱乐部新近打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB段和BC段均由不锈钢管材打造,总长度为26米,长方形CDEF为一木质平台的主视图.小敏经过现场测量得知:CD=1米,AD=15米,于是小敏大胆猜想立柱AB段的长为10米,请判断小敏的猜想是否正确?如果正确,请写出理由,如果错误,请求出立柱AB段的正确长度.
7.为了积极宣传防疫,南川区政府采用了移动车进行广播,如图,小明家在南大街这条笔直的公路MN的一侧点A处,小明家到公路MN的距离为600米,假使广播车P周围1000米以内能听到广播宣传,广播车P以250米/分的速度在公路MN上沿PN方向行驶时,若小明此时在家,他是否能听到?若能,请求出他总共能听到多长时间的广播?
答案
一、填空题
1.6,8;4.8. 2.18 3.9π.4.12cm. 5.. 6.9. 7..
二、选择题
1.D.2.B.3.B.4.D.5.B.6.D.7.D.8.A.9.D.10.B.
三、解答题
1.解:作AD⊥BC于D,
设CD=x,则BD=21﹣x,
在Rt△ACD中,AD2=AC2﹣CD2,
在Rt△ABD中,AD2=AB2﹣BD2,
∴AC2﹣CD2=AB2﹣BD2,即102﹣x2=172﹣(21﹣x)2,
解得,x=6,即CD=6,
则AD8,
△ABC的面积BC×AD21×8=84.
2.解:(1)大正方形的面积为:c2,中间小正方形面积为:(b﹣a)2;
四个直角三角形面积和为:4ab;
由图形关系可知:大正方形面积=小正方形面积+四直角三角形面积,
即有:c2=(b﹣a)2+4ab=b2﹣2ab+a2+2ab=a2+b2;
(2)如图示:
大正方形边长为(x+y)所以面积为:(x+y)2,它的面积也等于两个边长分别为x,y和两个长为x宽为y的矩形面积之和,即x2+2xy+y2
所以有:(x+y)2=x2+2xy+y2成立;
3.解:(1)梯形ABCD的面积为,
也可以表示为,∴,
即a2+b2=c2;
(2)在Rt△ABD中,AD2=AB2﹣BD2=42﹣x2=16﹣x2;
在Rt△ADC中,AD2=AC2﹣DC2=52﹣(6﹣x)2=﹣11+12x﹣x2;
所以16﹣x2=﹣11+12x﹣x2,
解得;
(3)如图,
由此可得(a+b)(a+2b)=a2+3ab+2b2.
4.解:依题意得AC=2,AE=3,
设原标杆的高为x,
∵∠A=90°,
∴由题中条件可得AB2+AC2=BC2,即AB2+22=(x﹣AB)2,
整理,得x2﹣2ABx=4,
同理,得(AB﹣0.5)2+32=(x﹣AB+0.5)2,
整理,得x2﹣2ABx+x=9,
解得x=5.
∴原来标杆的高度为5米.
5.解:在直角△ABO中,AB为斜边,已知AB=2.5米,BO=0.7米,
则根据勾股定理求得AO2.4(米),
∵A点下移0.4米,
∴A′O=2米,
在Rt△A′OB′中,已知A′B′=2.5米,A′O=2米,
则根据勾股定理B′O1.5(米),
∴BB′=OB′﹣BO=1.5﹣0.7=0.8(米),
所以梯子向外平移0.8米.
6.解:不正确;
理由:如答图,延长FC交AB于点G,
则CG⊥AB,AG=CD=1米,GC=AD=15米,
设BG=x米,则BC=(26﹣1﹣x)米,
在Rt△BGC中,
∵BG2+CG2=CB2,
∴x2+152=(26﹣1﹣x)2,
解得x=8,
∴BA=BG+GA=8+1=9(米),
∴小敏的猜想错误,立柱AB段的正确长度长为9米.
7.解:小明能听到宣传,
理由:∵村庄A到公路MN的距离为600米<1000米,
∴小明能听到宣传;
如图:假设当宣讲车行驶到P点开始小明听到广播,行驶到Q点小明听不到广播,
则AP=AQ=1000米,AB=600米,
∴BP=BQ800(米),∴PQ=1600米,
∴小明听到广播的时间为:1600÷250=6.4(分钟),
∴他总共能听到6.4分钟的广播.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
