北师大版七年级数学上册 第一章 丰富的图形世界 习题(word版含答案)
文档属性
| 名称 | 北师大版七年级数学上册 第一章 丰富的图形世界 习题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 286.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 00:00:00 | ||
图片预览

文档简介
《丰富的图形世界》习题
一、选择题
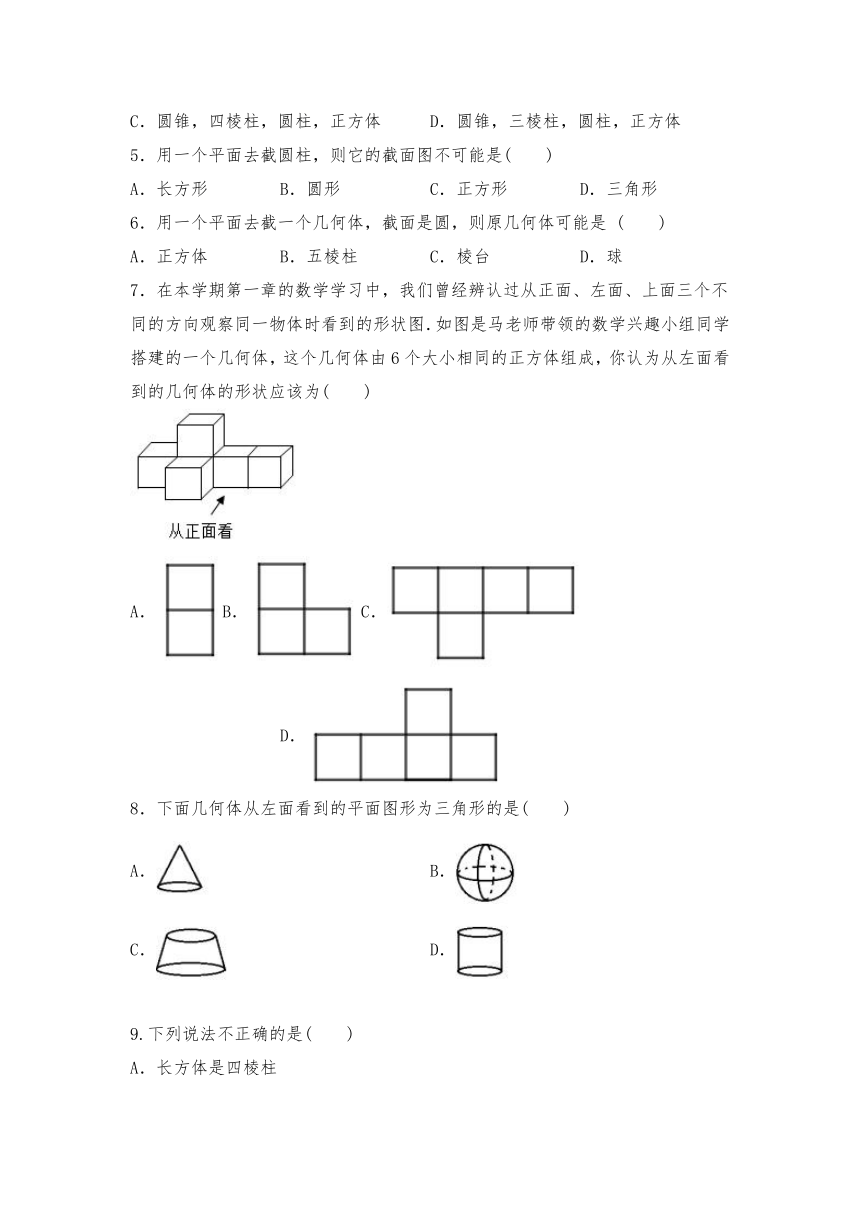
1.下列几何体中可以由平面图形绕某条直线旋转一周得到的是( )
A. B. C. D.
2.下列立体图形中,面数相同的是( )
①正方体;②圆柱;③四棱柱;④圆锥.
A.①② B.①③ C.②③ D.③④
3.如图所示的4个展开图中,不能做成没有顶盖的小方盒的是( )
A.B.C.D.
4.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
A.圆锥,三棱锥,圆柱,正方体 B.圆锥,四棱锥,圆柱,正方体
C.圆锥,四棱柱,圆柱,正方体 D.圆锥,三棱柱,圆柱,正方体
5.用一个平面去截圆柱,则它的截面图不可能是( )
A.长方形 B.圆形 C.正方形 D.三角形
6.用一个平面去截一个几何体,截面是圆,则原几何体可能是 ( )
A.正方体 B.五棱柱 C.棱台 D.球
7.在本学期第一章的数学学习中,我们曾经辨认过从正面、左面、上面三个不同的方向观察同一物体时看到的形状图.如图是马老师带领的数学兴趣小组同学搭建的一个几何体,这个几何体由6个大小相同的正方体组成,你认为从左面看到的几何体的形状应该为( )
A.B.C. D.
8.下面几何体从左面看到的平面图形为三角形的是( )
A. B.
C. D.
9.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
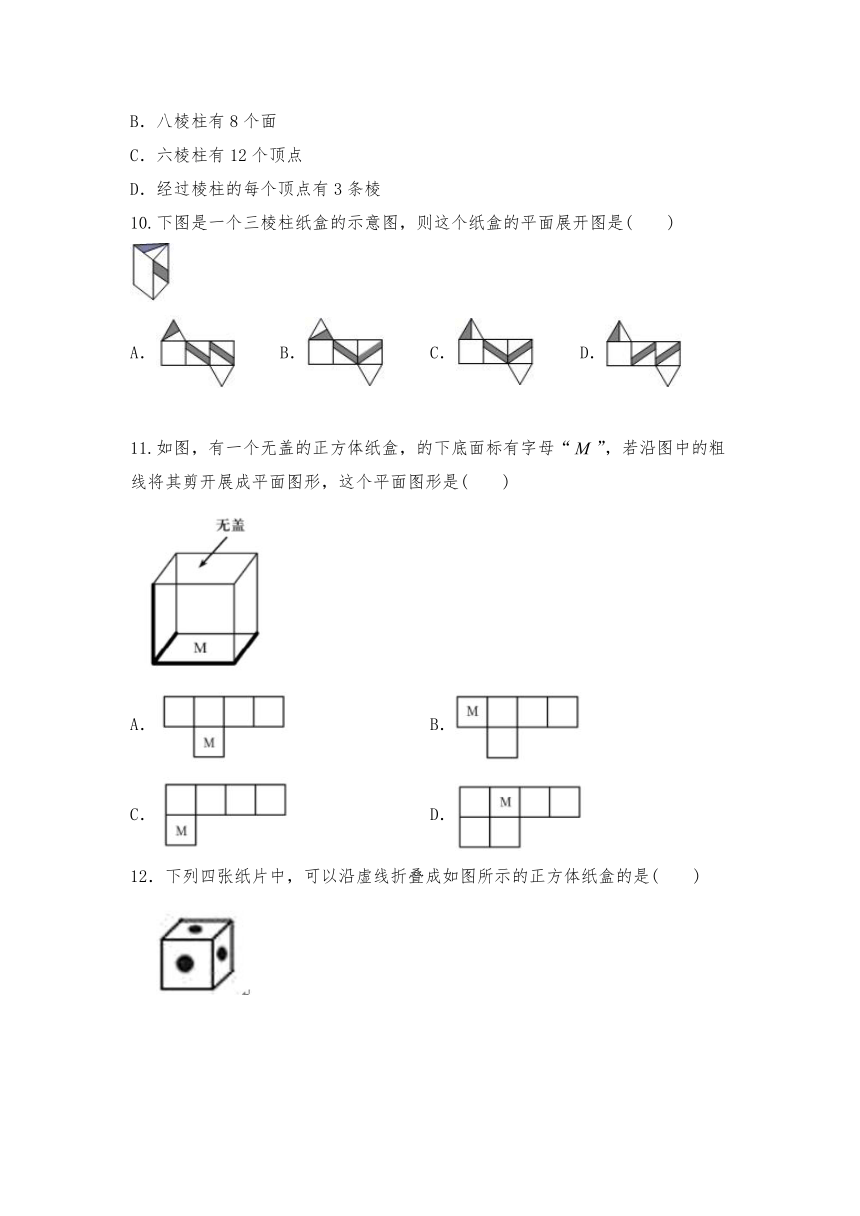
10.下图是一个三棱柱纸盒的示意图,则这个纸盒的平面展开图是( )
B. C. D.
11.如图,有一个无盖的正方体纸盒,的下底面标有字母“”,若沿图中的粗线将其剪开展成平面图形,这个平面图形是( )
A. B.
C. D.
12.下列四张纸片中,可以沿虚线折叠成如图所示的正方体纸盒的是( )
A. B. C. D.
二、填空题
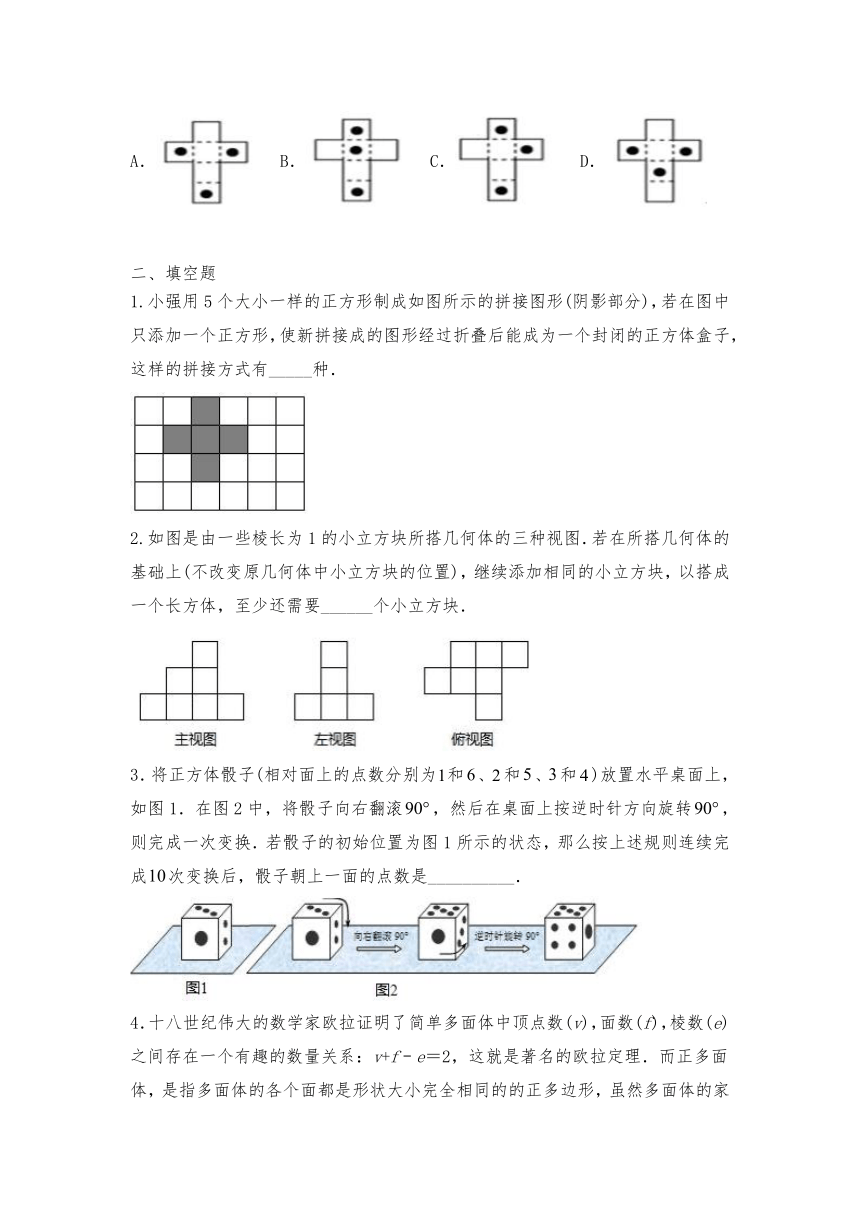
1.小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有_____种.
2.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
3.将正方体骰子(相对面上的点数分别为和、和、和)放置水平桌面上,如图1.在图2中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,则完成一次变换.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成次变换后,骰子朝上一面的点数是__________.
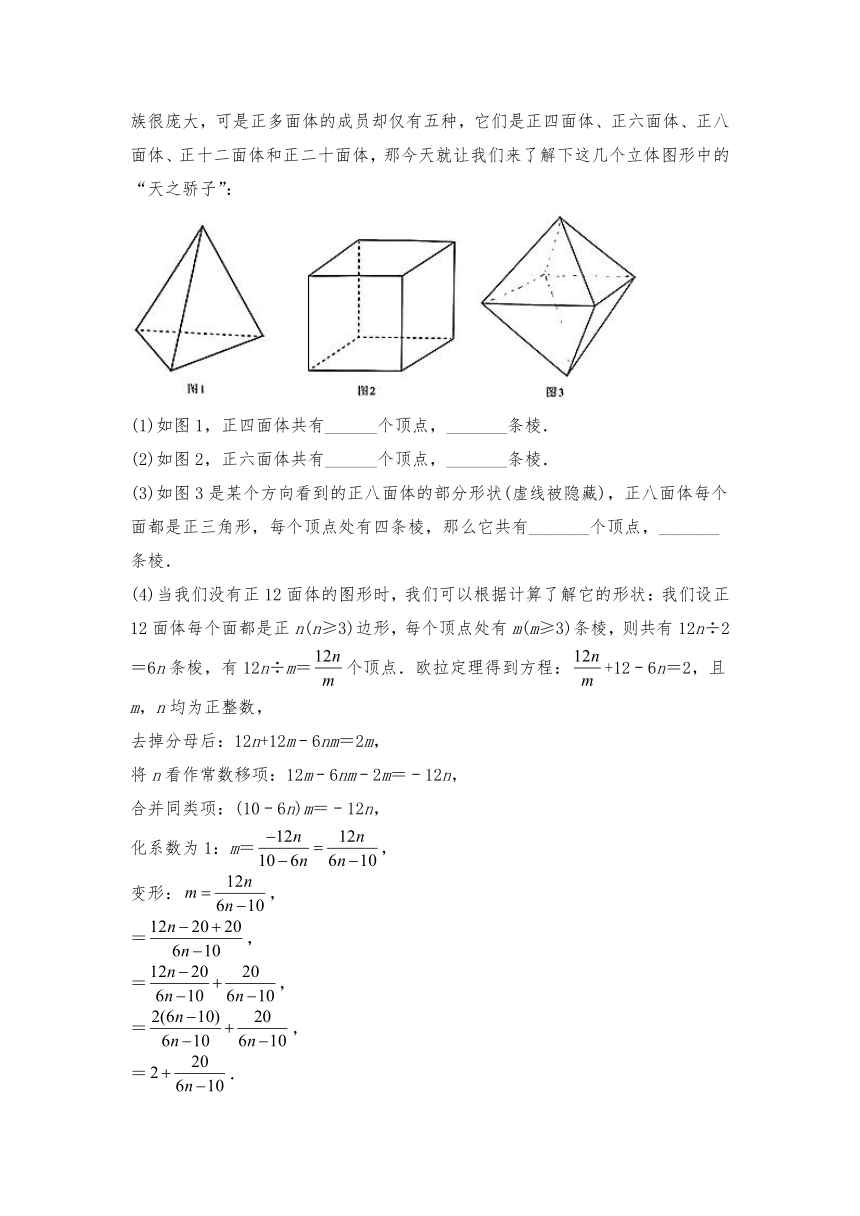
4.十八世纪伟大的数学家欧拉证明了简单多面体中顶点数(v),面数(f),棱数(e)之间存在一个有趣的数量关系:v+f﹣e=2,这就是著名的欧拉定理.而正多面体,是指多面体的各个面都是形状大小完全相同的的正多边形,虽然多面体的家族很庞大,可是正多面体的成员却仅有五种,它们是正四面体、正六面体、正八面体、正十二面体和正二十面体,那今天就让我们来了解下这几个立体图形中的“天之骄子”:
(1)如图1,正四面体共有______个顶点,_______条棱.
(2)如图2,正六面体共有______个顶点,_______条棱.
(3)如图3是某个方向看到的正八面体的部分形状(虚线被隐藏),正八面体每个面都是正三角形,每个顶点处有四条棱,那么它共有_______个顶点,_______条棱.
(4)当我们没有正12面体的图形时,我们可以根据计算了解它的形状:我们设正12面体每个面都是正n(n≥3)边形,每个顶点处有m(m≥3)条棱,则共有12n÷2=6n条梭,有12n÷m=个顶点.欧拉定理得到方程:+12﹣6n=2,且m,n均为正整数,
去掉分母后:12n+12m﹣6nm=2m,
将n看作常数移项:12m﹣6nm﹣2m=﹣12n,
合并同类项:(10﹣6n)m=﹣12n,
化系数为1:m=,
变形:,
=,
=,
=,
=.
分析:m(m≥3),n(n≥3)均为正整数,所以是正整数,所以n=5,m=3,即6n=30,.
因此正12面体每个面都是正五边形,共有30条棱,20个顶点.
请依据上面的方法或者根据自己的思考得出:正20面体共有_____条棱;_______个顶点.
三、解答题
1.由几个相同的棱长的小正方体搭成的几何体的俯视图如图所示,正方形中的数字表示该位置上小正方体的个数,在网格中画出这个几何体的主视图和左视图(注:网格中小正方形的边长等于小正方体的棱长)
2.在水平的桌面上,由若干个完全相同棱长为10cm的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图、左视图和俯视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的左视图和俯视图不变,在这个几何体上最多可以添加多少个小正方体?
(3)若给该几何体露在外面的面喷上红漆(不含几何体的底面),则需要喷漆的面积是多少cm2?
3.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
4.如图所示,在一张正方形纸片的四个角上各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子.请回答下列问题:
(1)剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为 ;
(2)如果设原来这张正方形纸片的边长为,所折成的无盖长方体盒子的高为,那么,这个无盖长方体盒子的容积可以表示为 ;
(3)如果原正方形纸片的边长为,剪去的小正方形的边长按整数值依次变化,即分别取
时,计算折成 的无盖长方体盒子的容积得到下表,由此可以判断,当剪去的小正方形边长为 时,折成的无盖长方体盒子的容积最大
剪去的小正方 形的边长 1 2 3 4 5 6 7 8 9 10
折成的无盖长方体的容积 324 576 500 384 252 128 36 0
答案
一、选择题
1.A.2.B.3.D4.D5.D.6.D7.B8.A9.B10.C.11.A.12.C.
二、填空题
1.3
2.26
3.5.
4.(1)4;6;(2)8;12;(3)6;12;(4)30;12.
三、解答题
1.解:如图所示:
2.解:(1)这个几何体的主视图和左视图如图:
(2)保持俯视图和左视图不变,可往第二列前面的几何体上放2个小正方体,后面的几何体上放1个小正方体,故最多可再添加3个正方体,
故答案为:3;
(3)10[(6+6)+6+2]=3200cm2
答:需要喷漆的面积是3200cm2.
3.(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为4;1;
(3)先算侧面--底层12个小面; 中层8个小面; 上层4个小面;
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1133=33cm2.
4.解:(1)由折叠可知,
剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为相等,
故答案为:相等;
(2)这个无盖长方体盒子的容积=h(a-2h)(a-2h)=h(a-2h)2(cm3);
故答案为:h(a-2h)2;
(3)当剪去的小正方形的边长取2时,m=2×(20-2×2)2=512,
当剪去的小正方形的边长取3时,n=3×(20-2×3)2=588,
当剪去的小正方形的边长的值逐渐增大时,所得到的无盖长方体纸盒的容积的值先增大后减小,
当剪去的小正方形的边长为3cm时,所得到的无盖长方体纸盒的容积最大.
故答案为:3.
一、选择题
1.下列几何体中可以由平面图形绕某条直线旋转一周得到的是( )
A. B. C. D.
2.下列立体图形中,面数相同的是( )
①正方体;②圆柱;③四棱柱;④圆锥.
A.①② B.①③ C.②③ D.③④
3.如图所示的4个展开图中,不能做成没有顶盖的小方盒的是( )
A.B.C.D.
4.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
A.圆锥,三棱锥,圆柱,正方体 B.圆锥,四棱锥,圆柱,正方体
C.圆锥,四棱柱,圆柱,正方体 D.圆锥,三棱柱,圆柱,正方体
5.用一个平面去截圆柱,则它的截面图不可能是( )
A.长方形 B.圆形 C.正方形 D.三角形
6.用一个平面去截一个几何体,截面是圆,则原几何体可能是 ( )
A.正方体 B.五棱柱 C.棱台 D.球
7.在本学期第一章的数学学习中,我们曾经辨认过从正面、左面、上面三个不同的方向观察同一物体时看到的形状图.如图是马老师带领的数学兴趣小组同学搭建的一个几何体,这个几何体由6个大小相同的正方体组成,你认为从左面看到的几何体的形状应该为( )
A.B.C. D.
8.下面几何体从左面看到的平面图形为三角形的是( )
A. B.
C. D.
9.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
10.下图是一个三棱柱纸盒的示意图,则这个纸盒的平面展开图是( )
B. C. D.
11.如图,有一个无盖的正方体纸盒,的下底面标有字母“”,若沿图中的粗线将其剪开展成平面图形,这个平面图形是( )
A. B.
C. D.
12.下列四张纸片中,可以沿虚线折叠成如图所示的正方体纸盒的是( )
A. B. C. D.
二、填空题
1.小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),若在图中只添加一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,这样的拼接方式有_____种.
2.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
3.将正方体骰子(相对面上的点数分别为和、和、和)放置水平桌面上,如图1.在图2中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,则完成一次变换.若骰子的初始位置为图1所示的状态,那么按上述规则连续完成次变换后,骰子朝上一面的点数是__________.
4.十八世纪伟大的数学家欧拉证明了简单多面体中顶点数(v),面数(f),棱数(e)之间存在一个有趣的数量关系:v+f﹣e=2,这就是著名的欧拉定理.而正多面体,是指多面体的各个面都是形状大小完全相同的的正多边形,虽然多面体的家族很庞大,可是正多面体的成员却仅有五种,它们是正四面体、正六面体、正八面体、正十二面体和正二十面体,那今天就让我们来了解下这几个立体图形中的“天之骄子”:
(1)如图1,正四面体共有______个顶点,_______条棱.
(2)如图2,正六面体共有______个顶点,_______条棱.
(3)如图3是某个方向看到的正八面体的部分形状(虚线被隐藏),正八面体每个面都是正三角形,每个顶点处有四条棱,那么它共有_______个顶点,_______条棱.
(4)当我们没有正12面体的图形时,我们可以根据计算了解它的形状:我们设正12面体每个面都是正n(n≥3)边形,每个顶点处有m(m≥3)条棱,则共有12n÷2=6n条梭,有12n÷m=个顶点.欧拉定理得到方程:+12﹣6n=2,且m,n均为正整数,
去掉分母后:12n+12m﹣6nm=2m,
将n看作常数移项:12m﹣6nm﹣2m=﹣12n,
合并同类项:(10﹣6n)m=﹣12n,
化系数为1:m=,
变形:,
=,
=,
=,
=.
分析:m(m≥3),n(n≥3)均为正整数,所以是正整数,所以n=5,m=3,即6n=30,.
因此正12面体每个面都是正五边形,共有30条棱,20个顶点.
请依据上面的方法或者根据自己的思考得出:正20面体共有_____条棱;_______个顶点.
三、解答题
1.由几个相同的棱长的小正方体搭成的几何体的俯视图如图所示,正方形中的数字表示该位置上小正方体的个数,在网格中画出这个几何体的主视图和左视图(注:网格中小正方形的边长等于小正方体的棱长)
2.在水平的桌面上,由若干个完全相同棱长为10cm的小正方体堆成一个几何体,如图所示.
(1)请你在方格纸中分别画出这个几何体的主视图、左视图和俯视图;
(2)若现在手头还有一些相同的小正方体,如果保持这个几何体的左视图和俯视图不变,在这个几何体上最多可以添加多少个小正方体?
(3)若给该几何体露在外面的面喷上红漆(不含几何体的底面),则需要喷漆的面积是多少cm2?
3.把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
4.如图所示,在一张正方形纸片的四个角上各剪去一个同样大小的正方形,然后把剩下的部分折成一个无盖的长方体盒子.请回答下列问题:
(1)剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为 ;
(2)如果设原来这张正方形纸片的边长为,所折成的无盖长方体盒子的高为,那么,这个无盖长方体盒子的容积可以表示为 ;
(3)如果原正方形纸片的边长为,剪去的小正方形的边长按整数值依次变化,即分别取
时,计算折成 的无盖长方体盒子的容积得到下表,由此可以判断,当剪去的小正方形边长为 时,折成的无盖长方体盒子的容积最大
剪去的小正方 形的边长 1 2 3 4 5 6 7 8 9 10
折成的无盖长方体的容积 324 576 500 384 252 128 36 0
答案
一、选择题
1.A.2.B.3.D4.D5.D.6.D7.B8.A9.B10.C.11.A.12.C.
二、填空题
1.3
2.26
3.5.
4.(1)4;6;(2)8;12;(3)6;12;(4)30;12.
三、解答题
1.解:如图所示:
2.解:(1)这个几何体的主视图和左视图如图:
(2)保持俯视图和左视图不变,可往第二列前面的几何体上放2个小正方体,后面的几何体上放1个小正方体,故最多可再添加3个正方体,
故答案为:3;
(3)10[(6+6)+6+2]=3200cm2
答:需要喷漆的面积是3200cm2.
3.(1)该几何体中正方体的个数为9+4+1=14个;
(2)根据图中小正方体的位置可知:最底层外边中间的小正方体被涂到2个面,共4个,只有最底层正中间的小正方体没被涂到,
故答案为4;1;
(3)先算侧面--底层12个小面; 中层8个小面; 上层4个小面;
再算上面--上层1个 中层3个(正方体是可以移动的,不管放在哪里,它压住的面积总是它的底面积,也就是一个,所以中层是4减1个)底层(9-4)=5个,
∴总共12+8+4+1+3+5=33个小面.
∴涂上颜色部分的总面积=1133=33cm2.
4.解:(1)由折叠可知,
剪去的小正方形的边长与折成的无盖长方体盒子的高之间的大小关系为相等,
故答案为:相等;
(2)这个无盖长方体盒子的容积=h(a-2h)(a-2h)=h(a-2h)2(cm3);
故答案为:h(a-2h)2;
(3)当剪去的小正方形的边长取2时,m=2×(20-2×2)2=512,
当剪去的小正方形的边长取3时,n=3×(20-2×3)2=588,
当剪去的小正方形的边长的值逐渐增大时,所得到的无盖长方体纸盒的容积的值先增大后减小,
当剪去的小正方形的边长为3cm时,所得到的无盖长方体纸盒的容积最大.
故答案为:3.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
