2022—-2023学年人教版数学七年级上册3.1.1一元一次方程 课件(共17张PPT)
文档属性
| 名称 | 2022—-2023学年人教版数学七年级上册3.1.1一元一次方程 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 553.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 19:11:59 | ||
图片预览






文档简介
(共17张PPT)
3.1.1 一元一次方程
第三章 一元一次方程
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (七年级 上)
知识与技能目标
认识方程的意义;了解方程思想进化过程;认知方程的定义,方程的元,方程的次数,方程的解,一元一次方程的判定。
过程与方法目标
通过熟悉算术到方程的演变过程,进而掌握用字母表示数和用字母表示未知数的思想。应用实际问题掌握列方程步骤,列式及寻找等量关系。
情感态度价值观
方程的应用是最切合生活现实的,让我们一起领略方程的简便和方程的特殊现实魅力。
学习目标
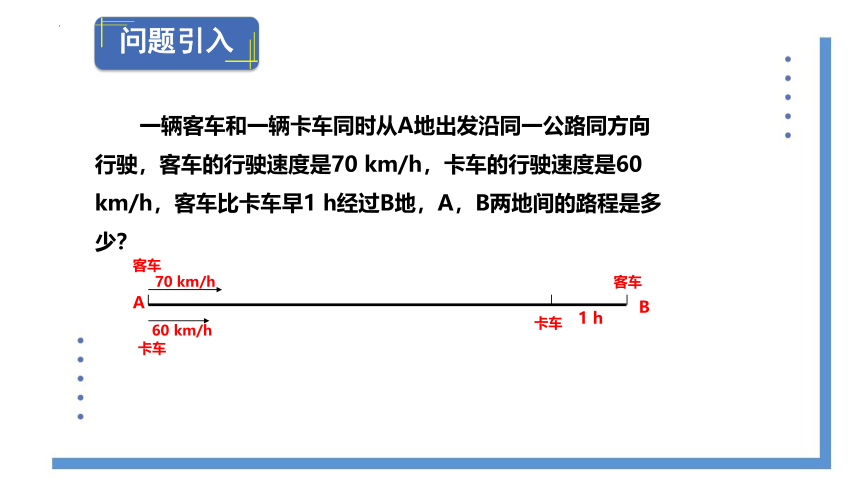
一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1 h经过B地,A,B两地间的路程是多少?
A
B
客车
卡车
客车
卡车
1 h
70 km/h
60 km/h
问题引入
(1)客车每小时比卡车每小时多行多少km?
(2)当客车到达B地时客车比卡车多走多少km?全程走了多少时间呢
(3)你能用算术的方法算出AB之间的路程了吗
A
B
客车
卡车
客车
卡车
1 h
70 km/h
60 km/h
70-60=10km
卡车1h的路程
一、方程及一元一次方程的概念
分析:
(1)上述问题中涉及到了哪些量?
一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1 h经过B地,A,B两地间的路程是多少?
自主学习
比较用算术方法和列方程解题的特点?
用算术方法解 用方程解
未知数不参加列式 未知数用字母表示来列式
根据题中的已知数和未知数间的关系,确定解答步骤,再列式计算 根据题意找出数量间的相等关系列出含有未知数的等式
提示:通常用x、y、z等字母表示未知数。
小组讨论
算术方法: 列出的算式表示解题的计算过程,其中只能 用已知数.对于较复杂的问题,列算式比较困难.
列方程(代数方法): 方程是根据题中的等量关系列出的等式.其中既含已知数,又含未知数.使问题的已知量与未知量之间的关系很容易表示,解决问题就比较方便.
所以,从算术到方程是数学的进步.
思考
方程
含有未知数的等式叫做方程.
知识要点
列方程解决实际问题步骤:
1.设字母表示未知数(通常用等字母x、y、z表示未知数);
2.根据问题中的相等关系,写出方方程.
归纳
答:(2)(3)是一元一次方程.
跟踪练习1
判断下列各式哪些是一元一次方程?
√
x
x
(1)2x-4=5x+3
(2) xy=1
(3) x2-3x+1=0
(4) 2x-4
(5) x=0
(6) 2x-4=4x-(2x-4)
x
√
√
跟踪练习2
对于方程4x=24,容易知道x=6可以使等式成立,对于方程170+15x=245,你知道x等于什么时,等式成立?我们来试一试.
请先填写下面的表格:
x 1 2 3 4 5 6 …
170+15x …
185
200
215
230
245
260
我们知道当x=5时,170+15x的值是245,所以方程
170+15x=245中的未知数的值应是5.
使方程等号左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
新知讲解
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
新知应用1
例1 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解?
(1)在式子:2x -1 ,1+7=2+6 , 1-3x = x +1 ,
x + 2y = 3,x2 +3x -1 = 0 中,方程有 个,
一元一次方程有 个。
(2)若方程 3 xn +4 = 5(x是未知数)是一元一次方
程,则 n = 。
(3)关于 x 的方程 (a -2)x 2 + a x + 1 = 0 是一元
一次方程,则 a = 。
3
1
1
2
新知应用2
1.一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两边都是整式,这样的方程叫做一元一次方程.
2.方程的解:
解方程就是求出使方程中等号两边相等的未知数的值,这个值就是方程的解.
方法归纳
必做作业:1.课本P84习题3.1第1-2
2.阅读课本P86阅读与理解
选做作业: 列方程解决问题
西安市出租车白天的收费标准为:起步价6元(即行驶距离不超过3千米都需付6元),行驶超过3千米以后,每增加1千米加收1.5元(不足1千米时按1千米计算).王明和李红乘坐这种出租车去博物馆参观,下车时他们交付了15元车费,那么他们搭乘出租车最多走了多少千米(不计等候时间)?
课后作业
同学们,下课
3.1.1 一元一次方程
第三章 一元一次方程
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (七年级 上)
知识与技能目标
认识方程的意义;了解方程思想进化过程;认知方程的定义,方程的元,方程的次数,方程的解,一元一次方程的判定。
过程与方法目标
通过熟悉算术到方程的演变过程,进而掌握用字母表示数和用字母表示未知数的思想。应用实际问题掌握列方程步骤,列式及寻找等量关系。
情感态度价值观
方程的应用是最切合生活现实的,让我们一起领略方程的简便和方程的特殊现实魅力。
学习目标
一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1 h经过B地,A,B两地间的路程是多少?
A
B
客车
卡车
客车
卡车
1 h
70 km/h
60 km/h
问题引入
(1)客车每小时比卡车每小时多行多少km?
(2)当客车到达B地时客车比卡车多走多少km?全程走了多少时间呢
(3)你能用算术的方法算出AB之间的路程了吗
A
B
客车
卡车
客车
卡车
1 h
70 km/h
60 km/h
70-60=10km
卡车1h的路程
一、方程及一元一次方程的概念
分析:
(1)上述问题中涉及到了哪些量?
一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1 h经过B地,A,B两地间的路程是多少?
自主学习
比较用算术方法和列方程解题的特点?
用算术方法解 用方程解
未知数不参加列式 未知数用字母表示来列式
根据题中的已知数和未知数间的关系,确定解答步骤,再列式计算 根据题意找出数量间的相等关系列出含有未知数的等式
提示:通常用x、y、z等字母表示未知数。
小组讨论
算术方法: 列出的算式表示解题的计算过程,其中只能 用已知数.对于较复杂的问题,列算式比较困难.
列方程(代数方法): 方程是根据题中的等量关系列出的等式.其中既含已知数,又含未知数.使问题的已知量与未知量之间的关系很容易表示,解决问题就比较方便.
所以,从算术到方程是数学的进步.
思考
方程
含有未知数的等式叫做方程.
知识要点
列方程解决实际问题步骤:
1.设字母表示未知数(通常用等字母x、y、z表示未知数);
2.根据问题中的相等关系,写出方方程.
归纳
答:(2)(3)是一元一次方程.
跟踪练习1
判断下列各式哪些是一元一次方程?
√
x
x
(1)2x-4=5x+3
(2) xy=1
(3) x2-3x+1=0
(4) 2x-4
(5) x=0
(6) 2x-4=4x-(2x-4)
x
√
√
跟踪练习2
对于方程4x=24,容易知道x=6可以使等式成立,对于方程170+15x=245,你知道x等于什么时,等式成立?我们来试一试.
请先填写下面的表格:
x 1 2 3 4 5 6 …
170+15x …
185
200
215
230
245
260
我们知道当x=5时,170+15x的值是245,所以方程
170+15x=245中的未知数的值应是5.
使方程等号左右两边相等的未知数的值叫方程的解.
求方程解的过程叫做解方程.
新知讲解
解:当x=1000时,
方程左边=0.52×1000-(1-0.52)×1000=520-480=40,
右边=80,左边≠右边,所以x=1000不是此方程的解.
当x=2000时,
方程左边= 0.52×2000-(1-0.52)×2000=1040-960=80,
右边=80,左边=右边,所以x=2000是此方程的解.
新知应用1
例1 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解?
(1)在式子:2x -1 ,1+7=2+6 , 1-3x = x +1 ,
x + 2y = 3,x2 +3x -1 = 0 中,方程有 个,
一元一次方程有 个。
(2)若方程 3 xn +4 = 5(x是未知数)是一元一次方
程,则 n = 。
(3)关于 x 的方程 (a -2)x 2 + a x + 1 = 0 是一元
一次方程,则 a = 。
3
1
1
2
新知应用2
1.一元一次方程的概念:
只含有一个未知数,未知数的次数是1,等号两边都是整式,这样的方程叫做一元一次方程.
2.方程的解:
解方程就是求出使方程中等号两边相等的未知数的值,这个值就是方程的解.
方法归纳
必做作业:1.课本P84习题3.1第1-2
2.阅读课本P86阅读与理解
选做作业: 列方程解决问题
西安市出租车白天的收费标准为:起步价6元(即行驶距离不超过3千米都需付6元),行驶超过3千米以后,每增加1千米加收1.5元(不足1千米时按1千米计算).王明和李红乘坐这种出租车去博物馆参观,下车时他们交付了15元车费,那么他们搭乘出租车最多走了多少千米(不计等候时间)?
课后作业
同学们,下课
