22.1.4 第1课时 二次函数y=ax2+bx+c的图象和性质 课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案)
文档属性
| 名称 | 22.1.4 第1课时 二次函数y=ax2+bx+c的图象和性质 课堂同步练(要点梳理+基础过关练+强化提升练+拓展延伸练+答案) |  | |
| 格式 | doc | ||
| 文件大小 | 477.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 13:43:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册课堂同步练
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第1课时 二次函数y=ax2+bx+c的图象和性质
要点梳理
1. 二次函数y=ax2+bx+c(a≠0)的图象是 ,对称轴是直线 ,顶点是 .
2. 二次函数y=ax2+bx+c的图象:如果a>0,当x<-时,y随x的增大而 ,当x>-时,y随x的增大而 ;如果a<0,当x<-时,y随x的增大而 ,当x>-时,y随x的增大而 .
3. 抛物线y=x2-2x-3的顶点坐标是 .
基础过关练
1. 抛物线y=x2-2x+m2+2(m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 将二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
A.y=(x-1)2+2 B.y=(x-1)2+3
C.y=(x-2)2+2 D.y=(x-2)2+4
3. 对于二次函数y=x2-2mx-3,下列结论错误的是( )
A.它的图象与x轴有两个交点 B.方程x2-2mx=3的两根之积为-3
C.它的图象的对称轴在y轴的右侧 D.x<m时,y随x的增大而减小
4. 把二次函数y=-2x2-4x+1配成y=a(x+h)2+k的形式为 ,所以其图象的开口向 ,对称轴是直线 ,顶点坐标为 .
5. 如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 .
6. 飞机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数解析式是s=60t-1.5t2,则飞机着陆后滑行的最长时间为 秒.
7. 已知二次函数y=-x2+2x+3.
(1)求函数图象的顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围.
强化提升练
8. 若函数y=(m-1)x2-6x+m的图象与x轴有且只有一个交点,则m的值为( )
A.-2或3 B.-2或-3 C.1或-2或3 D.1或-2或-3
9. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14 B.y=x2-8x+14 C.y=x2+4x+3 D.y=x2-4x+3
10. 点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1,y2,y3的大小关系是 .
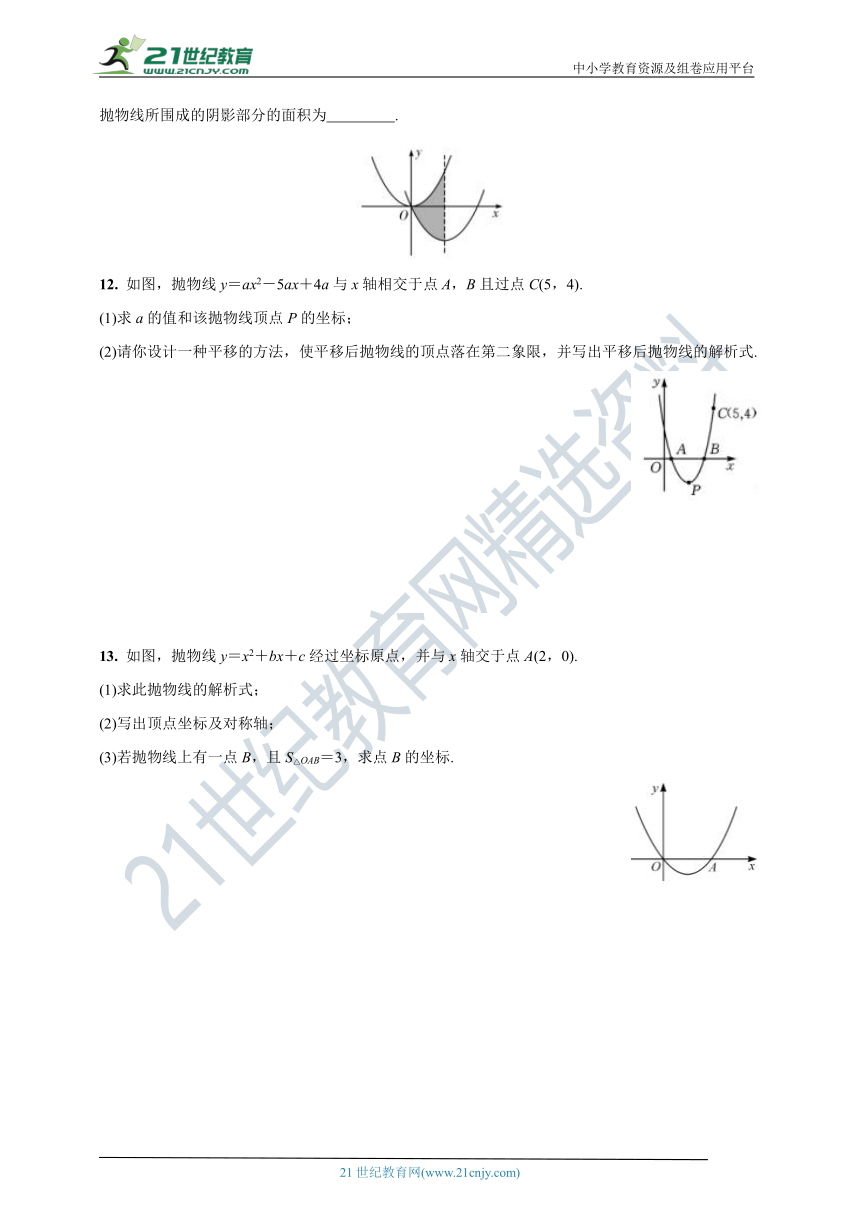
11. 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为 .
12. 如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.
13. 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
延伸拓展练
14. 如图,抛物线y=x2-3x+与x轴相交于A,B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
参 考 答 案
要点梳理
1. 抛物线 x=- (-,) 2. 减小 增大 增大 减小 3. (1,-4)
基础过关练
1. A 2. B 3. C
4. y=-2(x+1)2+3 下 x=-1 (-1,3)
5. (-2,0)
6. 20
7. 解:(1)∵y=-x2+2x+3=-(x-1)2+4,∴函数图象的顶点坐标为(1,4). 函数图象如图所示.
(2)根据图象可知:
①当-1<x<3时,函数值y为正数;
②当-2<x<2时,函数值y的取值范围是-5<y≤4.
强化提升练
8. C 9. A
10. y1=y2>y3
11. 4
12. 解:(1)把C(5,4)代入抛物线y=ax2-5ax+4a,得25a-25a+4a=4,解得a=1,∴该二次函数的解析式为y=x2-5x+4. ∵y=x2-5x+4=(x-)2-,∴顶点坐标为P(,-).
(2)(答案不唯一,合理即可)如:先向左平移3个单位,再向上平移4个单位,得到的二次函数的解析式为y=(x-+3)2-+4=(x+)2+,即y=x2+x+2.
13. 解:(1)把(0,0),(2,0)代入y=x2+bx+c,得解得∴解析式为y=x2-2x;
(2)∵y=x2-2x=(x-1)2-1,∴顶点为(1,-1),对称轴为直线x=1;
(3)设点B的坐标为(c,d),则×2|d|=3,解得d=3或d=-3. ∵顶点纵坐标为-1,-3<-1,(或x2-2x=-3无解)
∴d=3,∴x2-2x=3,解得x1=3,x2=-1,
∴点B的坐标为(3,3)或(-1,3).
延伸拓展练
14. 解:(1)令y=x2-3x+=0,可得x=或x=,∴A(,0),B(,0).令x=0,则y=,∴C(0,).设直线BC的解析式为y=kx+b,则 解得 ∴直线BC的解析式为y=-x+.
(2)设点D(m,m2-3m+),则E(m,-m+). 设DE的长度为d.∵点D是直线BC下方抛物线上一点,则d=-m+-(m2-3m+)=-m2+m=-(m-)2+. ∵a=-1<0,∴当m=时,d最大=. 此时D点的坐标为(,-).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学九年级上册课堂同步练
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第1课时 二次函数y=ax2+bx+c的图象和性质
要点梳理
1. 二次函数y=ax2+bx+c(a≠0)的图象是 ,对称轴是直线 ,顶点是 .
2. 二次函数y=ax2+bx+c的图象:如果a>0,当x<-时,y随x的增大而 ,当x>-时,y随x的增大而 ;如果a<0,当x<-时,y随x的增大而 ,当x>-时,y随x的增大而 .
3. 抛物线y=x2-2x-3的顶点坐标是 .
基础过关练
1. 抛物线y=x2-2x+m2+2(m是常数)的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2. 将二次函数y=x2-2x+4化为y=a(x-h)2+k的形式,下列正确的是( )
A.y=(x-1)2+2 B.y=(x-1)2+3
C.y=(x-2)2+2 D.y=(x-2)2+4
3. 对于二次函数y=x2-2mx-3,下列结论错误的是( )
A.它的图象与x轴有两个交点 B.方程x2-2mx=3的两根之积为-3
C.它的图象的对称轴在y轴的右侧 D.x<m时,y随x的增大而减小
4. 把二次函数y=-2x2-4x+1配成y=a(x+h)2+k的形式为 ,所以其图象的开口向 ,对称轴是直线 ,顶点坐标为 .
5. 如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 .
6. 飞机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数解析式是s=60t-1.5t2,则飞机着陆后滑行的最长时间为 秒.
7. 已知二次函数y=-x2+2x+3.
(1)求函数图象的顶点坐标,并画出这个函数的图象;
(2)根据图象,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围.
强化提升练
8. 若函数y=(m-1)x2-6x+m的图象与x轴有且只有一个交点,则m的值为( )
A.-2或3 B.-2或-3 C.1或-2或3 D.1或-2或-3
9. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14 B.y=x2-8x+14 C.y=x2+4x+3 D.y=x2-4x+3
10. 点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1,y2,y3的大小关系是 .
11. 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2-2x,其对称轴与两段抛物线所围成的阴影部分的面积为 .
12. 如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.
13. 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
(1)求此抛物线的解析式;
(2)写出顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.
延伸拓展练
14. 如图,抛物线y=x2-3x+与x轴相交于A,B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
参 考 答 案
要点梳理
1. 抛物线 x=- (-,) 2. 减小 增大 增大 减小 3. (1,-4)
基础过关练
1. A 2. B 3. C
4. y=-2(x+1)2+3 下 x=-1 (-1,3)
5. (-2,0)
6. 20
7. 解:(1)∵y=-x2+2x+3=-(x-1)2+4,∴函数图象的顶点坐标为(1,4). 函数图象如图所示.
(2)根据图象可知:
①当-1<x<3时,函数值y为正数;
②当-2<x<2时,函数值y的取值范围是-5<y≤4.
强化提升练
8. C 9. A
10. y1=y2>y3
11. 4
12. 解:(1)把C(5,4)代入抛物线y=ax2-5ax+4a,得25a-25a+4a=4,解得a=1,∴该二次函数的解析式为y=x2-5x+4. ∵y=x2-5x+4=(x-)2-,∴顶点坐标为P(,-).
(2)(答案不唯一,合理即可)如:先向左平移3个单位,再向上平移4个单位,得到的二次函数的解析式为y=(x-+3)2-+4=(x+)2+,即y=x2+x+2.
13. 解:(1)把(0,0),(2,0)代入y=x2+bx+c,得解得∴解析式为y=x2-2x;
(2)∵y=x2-2x=(x-1)2-1,∴顶点为(1,-1),对称轴为直线x=1;
(3)设点B的坐标为(c,d),则×2|d|=3,解得d=3或d=-3. ∵顶点纵坐标为-1,-3<-1,(或x2-2x=-3无解)
∴d=3,∴x2-2x=3,解得x1=3,x2=-1,
∴点B的坐标为(3,3)或(-1,3).
延伸拓展练
14. 解:(1)令y=x2-3x+=0,可得x=或x=,∴A(,0),B(,0).令x=0,则y=,∴C(0,).设直线BC的解析式为y=kx+b,则 解得 ∴直线BC的解析式为y=-x+.
(2)设点D(m,m2-3m+),则E(m,-m+). 设DE的长度为d.∵点D是直线BC下方抛物线上一点,则d=-m+-(m2-3m+)=-m2+m=-(m-)2+. ∵a=-1<0,∴当m=时,d最大=. 此时D点的坐标为(,-).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
