22.3实际问题与二次函数 自主学习同步练习题 2022-2023学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 22.3实际问题与二次函数 自主学习同步练习题 2022-2023学年人教版九年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 08:54:38 | ||
图片预览




文档简介
2022-2023学年人教版九年级数学上册《22.3实际问题与二次函数》
自主学习同步练习题(附答案)
一.选择题
1.长方形的周长为12cm,其中一边为x(0<x<6)cm,面积为ycm2.那么y与x的关系是( )
A.y=(12﹣x)2 B.y=(6﹣x)2 C.y=x(12﹣x) D.y=x(6﹣x)
2.若二次函数y=ax2﹣bx+2有最大值6,则y=﹣a(x+1)2+bx+b+2的最小值为( )
A.﹣1 B.﹣2 C.﹣6 D.2
3.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
4.一身高1.8m的篮球运动员在距篮板AB=4m(DE与AB的水平距离)处跳起投篮,球在运动员头顶上方0.25m处出手,在如图所示的直角坐标系中,球在空中运行的路线可以用y=﹣0.2x2+3.5来描述,那么球出手时,运动员跳离地面的高度为( )
A.0.1 B.0.15 C.0.2 D.0.25
5.如图,某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN,其中点P在AC上,点NM分别在BCAB上,记PM=x,PN=y,图中阴影部分的面积为S,若NP在一定范围内变化,则y与x,S与x满足的函数关系分别是( )
A.反比例函数关系,一次函数关系
B.二次函数关系,一次函数关系
C.一次函数关系,反比例函数关系
D.一次函数关系,二次函数关系
6.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线C1:y=﹣x2+x+30近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.那么当运动员滑出点A后,运动员运动的水平距离为( )米时,运动员与小山坡C1的竖直距离为20米.
A.50 B. C. D.
7.一款畅销商品的销售价格为m元,一个月可以获利(m﹣8)(900﹣15m).下列表达式中可以直接看出最大获利润和此时销售价格的是( )
A.﹣15(m﹣34)2+10140 B.(m﹣8)(900﹣15m)
C.﹣15m2+1020m﹣7200 D.﹣15(m﹣60)(m﹣8)
8.已知二次函数y=2x2﹣4x﹣1在0≤x≤a时,y取得的最大值为15,则a的值为( )
A.1 B.2 C.3 D.4
9.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是( )
A.s≥3 B.3<s<8 C.s≤3 D.s≥8
10.如图,始终盛满水的圆柱体水桶水面离地面的高度为20cm,如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为.如果想通过垫高水桶,使射出水的最大射程增加10cm,则小孔离水面的距离是( )
A.14cm B.15cm C.16cm D.18cm
二.填空题
11.如图是一个横断面为抛物线形状的拱桥,此时水面宽AB为3米,拱桥最高点C离水面的距离CO也为3米,则当水位上升1米后,水面的宽度为 米.
12.已知函数y=mx2+2mx+1在﹣3≤x≤2上有最大值4,则常数m的值为 .
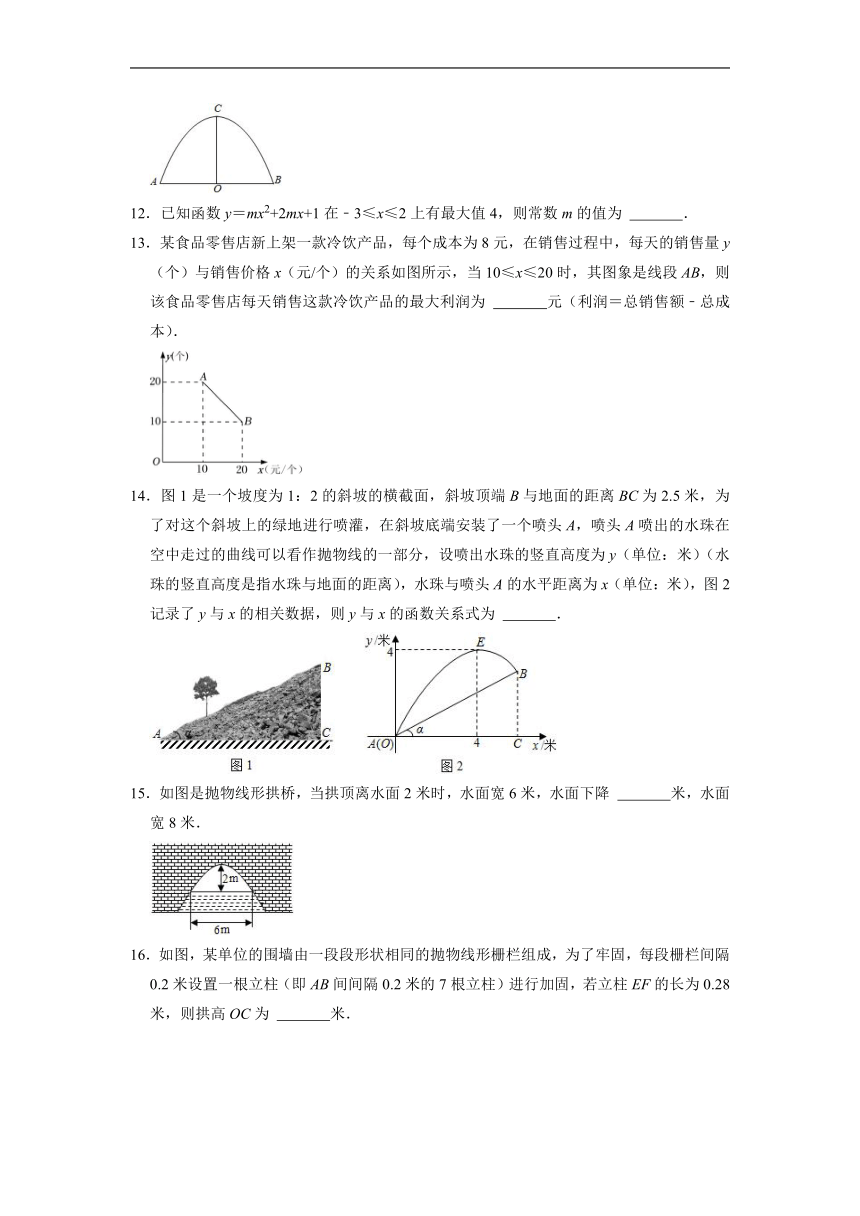
13.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为 元(利润=总销售额﹣总成本).
14.图1是一个坡度为1:2的斜坡的横截面,斜坡顶端B与地面的距离BC为2.5米,为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分,设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),图2记录了y与x的相关数据,则y与x的函数关系式为 .
15.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降 米,水面宽8米.
16.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为 米.
17.图1是一座彩虹桥两条抛物线型钢梁在桥面上的跨度分别为AB=50米和CD=40米(如图2所示),x轴表示桥面,BC=10米.若两抛物线交y轴于同一点,且它们的形状相同,则的值为 .
三.解答题
18.先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴代数式y2+4y+8的最小值为4.
(1)求代数式x2﹣6x+11的最小值;
(2)若a2+2a+1+|b﹣2022|=0,则ab= .
(3)某居民小区要在一块一边靠墙(墙长15米)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20米的栅栏围成.如图,设AB=x米,请问:当x取何值时,花园的面积最大?最大面积是多少?
19.某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?
(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?
20.如图1,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m).如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5m.
①求上边缘抛物线的函数解析式,并求喷出水的最大射程OC;
②求下边缘抛物线与x轴的正半轴交点B的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
(2)若EF=1m.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
参考答案
一.选择题
1.解:∵长方形的周长为12cm,其中一边长为xcm,
∴另一边长为(6﹣x)cm,
面积y=x(6﹣x),
故选:D.
2.解:∵二次函数y=ax2﹣bx+2有最大值6,
∴设二次函数y=ax2﹣bx+2的顶点坐标为(m,6),
平移可知y=a(x+1)2﹣b(x+1)+2的顶点坐标为(m﹣1,6),
根据关于x轴对称可知,y=﹣a(x+1)2+bx+b﹣2的顶点坐标为(m﹣1,﹣6),且开口向上,
再向上平移4个单位得到y=﹣a(x+1)2+bx+b+2,
此时顶点坐标为(m﹣1,﹣2),最小值为﹣2,
故答案为:B.
3.解:把A代入得:
=﹣×9+k,
∴k=,
∴y=﹣(x﹣3)2+,
令y=0得﹣(x﹣3)2+=0,
解得x=﹣2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故选:C.
4.解:当y=3.05时,
即3.05=﹣0.2x2+3.5,
解得:x=1.5m,
∴4﹣1.5=2.5,
当x=﹣2.5时,y=﹣0.2×(﹣2.5)2+3.5=2.25,
∴2.25﹣0.25﹣1.8=0.2m,
答:球出手时,他跳离地面的高度为0.2m.
故选:C.
5.解:设AB=m(m为常数),
在△AMP中,∠A=45°,AM⊥PM,
∴△AMP为等腰直角三角形,
∴AM=PM,
∵四边形PMBN是矩形,
∴PN=BM,
∴x+y=PM+PN=AM+BM=AB=m,
即y=﹣x+m,
∴y与x成一次函数关系,
∵S=S△ABC﹣S矩形PMBN=m2﹣xy=m2﹣x(﹣x+m)=x 2﹣m x+m2,
∴S与x成二次函数关系.
故选:D.
6.解:把(0,50)、(60,60)代入y=﹣x2+bx+c,
得
解得
∴抛物线C2所对应的函数表达式y=﹣x2+x+50;
设运动员运动的水平距离是x米,此时小山坡的高度是y=﹣x2+x+30,运动员运动的水平高度是y=﹣x2+x+50,
∴﹣x2+x+50=﹣x2+x+30+20,
解得x=或0(舍去),
答:运动员运动的水平距离为米时,运动员与小山坡C1的竖直距离为20米,
故选:C.
7.解:根据题意,设一个月可以获利为y元,则y=(m﹣8)(900﹣15m),
=﹣15(m﹣34)2+10140,
根据顶点式直接看出最大获利润和此时销售价格,
故选:A.
8.解:∵二次函数y=2x2﹣4x﹣1=2(x﹣1)2﹣3,
∴抛物线的对称轴为x=1,顶点(1,﹣3),
∴当y=﹣3时,x=1,
当y=15时,2(x﹣1)2﹣3=15,
解得x=4或x=﹣2,
∵当0≤x≤a时,y的最大值为15,
∴a=4,
故选:D.
9.解:∵x+y2=3,
∴y2=3﹣x,
∵3﹣x≥0,
∴x≤3,
∴s=x2+8y2=x2+8(3﹣x)=x2﹣8x+24=(x﹣4)2+8,
∴s≥9.
故选:D.
10.解:∵s=,
∴s2=4h(20﹣h)=﹣4(h﹣10)2+400,
∴当h为10cm时,射程s有最大值,最大射程是20cm.
设垫高的高度为m,则s2=4h(20+m﹣h)=﹣4(h﹣)2+(20+m)2,
∴当h=cm时,s最大为20+m=20+10,
∴m=10cm,此时h==15cm.
∴小孔离水面的竖直距离为15cm.
故选:B.
二.填空题
11.解:如右图所示,建立平面直角坐标系,
设抛物线的解析式为:y=ax2+3,
∵函数图象过点A(﹣,0),
∴0=a(﹣)2+3,
解得:a=﹣,
∴抛物线的解析式为:y=﹣x2+3,
当y=1时,1=﹣x2+3,
解得:x1=,x2=﹣(舍去),
∴水面的宽度是:米.
故答案为:.
12.解:y=mx2+2mx+1=m(x+1)2﹣m.
当m>0时,
当x=2时,y有最大值,
∴4m+4m+1=4,
∴m=;
当m<0时,
当x=﹣1时,y有最大值,
∴m﹣2m+1=4,
∴m=﹣3,
综上所述:m的值为或﹣3.
故答案是:或﹣3.
13.解:当10≤x≤20时,设y=kx+b,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为y=﹣x+30,
设该食品零售店每天销售这款冷饮产品的利润为w元,
w=(x﹣8)y=(x﹣8)(﹣x+30)=﹣x2+38x﹣240=﹣(x﹣19)2+121,
∵﹣1<0,
∴当x=19时,w有最大值为121,
故答案为:121.
14.解:由图2可知,函数图象的对称轴为x=4,最大值为4,设函数的解析式为y=a(x﹣4)2+4,
将点(0,0)代入得,16a+4=0,
解得:a=﹣,
∴y与x的函数关系式为y=﹣(x﹣4)2+4.
故答案为:y=﹣(x﹣4)2+4.
15.解:以水面所在的直线AB为x轴,以过拱顶C且垂直于AB的直线为y轴建立平面直角坐标系,O为原点,
由题意可得:AO=OB=3米,C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,
把A点坐标(﹣3,0)代入抛物线解析式得,
9a+2=0,
解得:a=﹣,
所以抛物线解析式为y=﹣x2+2,
当x=4时,y=﹣×16+2=﹣,
∴水面下降米,
故答案为:.
16.解:根据题意可知,AB=0.2×8=1.6,以O坐标系的原点,OC所在直线为y轴建立坐标系,如图所示,
设抛物线解析式为y=ax2+bx+c,
∴抛物线过(0.8,0)、(﹣0.8,0)、(﹣0.6,﹣0.28),
∴,
解得.
∴抛物线解析式为y=x2+0.64.
令x=0,则y=0.64.
∴OC=0.64.
故答案为:0.64.
17.解:因为两个抛物线形状相同,可设:yAB=m(x﹣xA)(x﹣xB)①,yCD=m(x﹣xC)(x﹣xD)②,其中xA,xB,xC,xD分别为A,B,C,D的横坐标,
对于①令x=0,则y=mxA xB,
所以E点坐标为(0,mxAxB);
同理,对于②令x=0,则y=mxC xD,
所以E点坐标为(0,mxCxD),
因为mxAxB=mxCxD,即xAxB=xCxD,
因为AB=50米,BC=10米,CD=40米.
所以AC=60米,
所以xC﹣xA=60,xC﹣xB=10,xD﹣xC=40,
所以xA=xC﹣60,xB=xC﹣10,xD=xC十40,
将上式代入xAxB=xCxD得,
(xC60)(xC﹣10)=xC(xC40),
解得xC=,
又因为xB=﹣,
所以=﹣=.
故答案为:.
三.解答题
18.解:(1)x2﹣6x+11=(x﹣3)2+2,
∵(x﹣3)2≥0,
∴(x﹣3)2+2≥2,
∴代数式x2﹣6x+11的最小值为2;
(2)∵a2+2a+1+|b﹣2022|=0,
∴(a+1)2+|b﹣2022|=0,
∴a+1=0,b﹣2022=0,
∴a=﹣1,b=2022,
∴ab=(﹣1)2022=1,
故答案为:1;
(3)设花园的面积为ym2,由题意可得,
y=x(20﹣2x)=﹣2x2+20x=﹣2(x2﹣10x)=﹣2(x﹣5)2+50,
∵﹣2<0,
∴当x=5时,y最大,最大值为50,
此时BC的长是20﹣2×5=10<15,
∴当x=5时,花园的面积最大,最大面积是50m2.
19.解:(1)设一次函数的关系式为y=kx+b,
由题图可知,函数图象过点(25,50)和点(35,30).
把这两点的坐标代入一次函数y=kx+b,
得,
解得,
∴一次函数的关系式为y=﹣2x+100;
(2)根据题意,设当天玩具的销售单价是x元,
由题意得,
(x﹣10)×(﹣2x+100)=600,
解得:x1=40,x2=20,
∴当天玩具的销售单价是40元或20元;
(3)根据题意,则w=(x﹣10)×(﹣2x+100),
整理得:w=﹣2(x﹣30)2+800;
∵﹣2<0,
∴当x=30时,w有最大值,最大值为800;
∴当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元.
20.解:(1)①如图1,由题意得A(2,2)是上边缘抛物线的顶点,
设y=a(x﹣2)2+2,
又∵抛物线过点(0,1.5),
∴1.5=4a+2,
∴a=﹣,
∴上边缘抛物线的函数解析式为y=﹣(x﹣2)2+2,
当y=0时,0=﹣(x﹣2)2+2,
解得x1=6,x2=﹣2(舍去),
∴喷出水的最大射程OC为6m;
②∵对称轴为直线x=2,
∴点(0,1.5)的对称点为(4,1.5),
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的,
∴点B的坐标为(2,0);
③∵EF=0.5,
∴点F的纵坐标为0.5,
∴0.5=﹣(x﹣2)2+2,
解得x=2±2,
∵x>0,
∴x=2+2,
当x>2时,y随x的增大而减小,
∴当2≤x≤6时,要使y≥0.5,
则x≤2+2,
∵当0≤x≤2时,y随x的增大而增大,且x=0时,y=1.5>0.5,
∴当0≤x≤6时,要使y≥0.5,则0≤x≤2+2,
∵DE=3,灌溉车行驶时喷出的水能浇灌到整个绿化带,
∴d的最大值为2+2﹣3=2﹣1,
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是OB≤d,
∴d的最小值为2,
综上所述,d的取值范围是2≤d≤2﹣1;
(2)当喷水口高度最低,且恰好能浇灌到整个绿化带时,点D、F恰好分别在两条抛物线上,
故设点D(m,﹣(m+2)2+h+0.5),F(m+3,﹣[(m+3﹣2)2+h+0.5]),
则有﹣(m+3﹣2)2+h+0.5﹣[﹣(m+2)2+h+0.5]=1,
解得m=2.5,
∴点D的纵坐标为h﹣,
∴h﹣=0,
∴h的最小值为.
自主学习同步练习题(附答案)
一.选择题
1.长方形的周长为12cm,其中一边为x(0<x<6)cm,面积为ycm2.那么y与x的关系是( )
A.y=(12﹣x)2 B.y=(6﹣x)2 C.y=x(12﹣x) D.y=x(6﹣x)
2.若二次函数y=ax2﹣bx+2有最大值6,则y=﹣a(x+1)2+bx+b+2的最小值为( )
A.﹣1 B.﹣2 C.﹣6 D.2
3.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
4.一身高1.8m的篮球运动员在距篮板AB=4m(DE与AB的水平距离)处跳起投篮,球在运动员头顶上方0.25m处出手,在如图所示的直角坐标系中,球在空中运行的路线可以用y=﹣0.2x2+3.5来描述,那么球出手时,运动员跳离地面的高度为( )
A.0.1 B.0.15 C.0.2 D.0.25
5.如图,某公司准备在一个等腰直角三角形ABC的绿地上建造一个矩形的休闲书吧PMBN,其中点P在AC上,点NM分别在BCAB上,记PM=x,PN=y,图中阴影部分的面积为S,若NP在一定范围内变化,则y与x,S与x满足的函数关系分别是( )
A.反比例函数关系,一次函数关系
B.二次函数关系,一次函数关系
C.一次函数关系,反比例函数关系
D.一次函数关系,二次函数关系
6.北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线C1:y=﹣x2+x+30近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.那么当运动员滑出点A后,运动员运动的水平距离为( )米时,运动员与小山坡C1的竖直距离为20米.
A.50 B. C. D.
7.一款畅销商品的销售价格为m元,一个月可以获利(m﹣8)(900﹣15m).下列表达式中可以直接看出最大获利润和此时销售价格的是( )
A.﹣15(m﹣34)2+10140 B.(m﹣8)(900﹣15m)
C.﹣15m2+1020m﹣7200 D.﹣15(m﹣60)(m﹣8)
8.已知二次函数y=2x2﹣4x﹣1在0≤x≤a时,y取得的最大值为15,则a的值为( )
A.1 B.2 C.3 D.4
9.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是( )
A.s≥3 B.3<s<8 C.s≤3 D.s≥8
10.如图,始终盛满水的圆柱体水桶水面离地面的高度为20cm,如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为.如果想通过垫高水桶,使射出水的最大射程增加10cm,则小孔离水面的距离是( )
A.14cm B.15cm C.16cm D.18cm
二.填空题
11.如图是一个横断面为抛物线形状的拱桥,此时水面宽AB为3米,拱桥最高点C离水面的距离CO也为3米,则当水位上升1米后,水面的宽度为 米.
12.已知函数y=mx2+2mx+1在﹣3≤x≤2上有最大值4,则常数m的值为 .
13.某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当10≤x≤20时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为 元(利润=总销售额﹣总成本).
14.图1是一个坡度为1:2的斜坡的横截面,斜坡顶端B与地面的距离BC为2.5米,为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分,设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),图2记录了y与x的相关数据,则y与x的函数关系式为 .
15.如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降 米,水面宽8米.
16.如图,某单位的围墙由一段段形状相同的抛物线形栅栏组成,为了牢固,每段栅栏间隔0.2米设置一根立柱(即AB间间隔0.2米的7根立柱)进行加固,若立柱EF的长为0.28米,则拱高OC为 米.
17.图1是一座彩虹桥两条抛物线型钢梁在桥面上的跨度分别为AB=50米和CD=40米(如图2所示),x轴表示桥面,BC=10米.若两抛物线交y轴于同一点,且它们的形状相同,则的值为 .
三.解答题
18.先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴代数式y2+4y+8的最小值为4.
(1)求代数式x2﹣6x+11的最小值;
(2)若a2+2a+1+|b﹣2022|=0,则ab= .
(3)某居民小区要在一块一边靠墙(墙长15米)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20米的栅栏围成.如图,设AB=x米,请问:当x取何值时,花园的面积最大?最大面积是多少?
19.某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?
(3)设该玩具日销售利润为w元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?
20.如图1,灌溉车沿着平行于绿化带底部边线l的方向行驶,为绿化带浇水.喷水口H离地竖直高度为h(单位:m).如图2,可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度为EF的长.下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.5m,灌溉车到l的距离OD为d(单位:m).
(1)若h=1.5,EF=0.5m.
①求上边缘抛物线的函数解析式,并求喷出水的最大射程OC;
②求下边缘抛物线与x轴的正半轴交点B的坐标;
③要使灌溉车行驶时喷出的水能浇灌到整个绿化带,求d的取值范围.
(2)若EF=1m.要使灌溉车行驶时喷出的水能浇灌到整个绿化带,请直接写出h的最小值.
参考答案
一.选择题
1.解:∵长方形的周长为12cm,其中一边长为xcm,
∴另一边长为(6﹣x)cm,
面积y=x(6﹣x),
故选:D.
2.解:∵二次函数y=ax2﹣bx+2有最大值6,
∴设二次函数y=ax2﹣bx+2的顶点坐标为(m,6),
平移可知y=a(x+1)2﹣b(x+1)+2的顶点坐标为(m﹣1,6),
根据关于x轴对称可知,y=﹣a(x+1)2+bx+b﹣2的顶点坐标为(m﹣1,﹣6),且开口向上,
再向上平移4个单位得到y=﹣a(x+1)2+bx+b+2,
此时顶点坐标为(m﹣1,﹣2),最小值为﹣2,
故答案为:B.
3.解:把A代入得:
=﹣×9+k,
∴k=,
∴y=﹣(x﹣3)2+,
令y=0得﹣(x﹣3)2+=0,
解得x=﹣2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故选:C.
4.解:当y=3.05时,
即3.05=﹣0.2x2+3.5,
解得:x=1.5m,
∴4﹣1.5=2.5,
当x=﹣2.5时,y=﹣0.2×(﹣2.5)2+3.5=2.25,
∴2.25﹣0.25﹣1.8=0.2m,
答:球出手时,他跳离地面的高度为0.2m.
故选:C.
5.解:设AB=m(m为常数),
在△AMP中,∠A=45°,AM⊥PM,
∴△AMP为等腰直角三角形,
∴AM=PM,
∵四边形PMBN是矩形,
∴PN=BM,
∴x+y=PM+PN=AM+BM=AB=m,
即y=﹣x+m,
∴y与x成一次函数关系,
∵S=S△ABC﹣S矩形PMBN=m2﹣xy=m2﹣x(﹣x+m)=x 2﹣m x+m2,
∴S与x成二次函数关系.
故选:D.
6.解:把(0,50)、(60,60)代入y=﹣x2+bx+c,
得
解得
∴抛物线C2所对应的函数表达式y=﹣x2+x+50;
设运动员运动的水平距离是x米,此时小山坡的高度是y=﹣x2+x+30,运动员运动的水平高度是y=﹣x2+x+50,
∴﹣x2+x+50=﹣x2+x+30+20,
解得x=或0(舍去),
答:运动员运动的水平距离为米时,运动员与小山坡C1的竖直距离为20米,
故选:C.
7.解:根据题意,设一个月可以获利为y元,则y=(m﹣8)(900﹣15m),
=﹣15(m﹣34)2+10140,
根据顶点式直接看出最大获利润和此时销售价格,
故选:A.
8.解:∵二次函数y=2x2﹣4x﹣1=2(x﹣1)2﹣3,
∴抛物线的对称轴为x=1,顶点(1,﹣3),
∴当y=﹣3时,x=1,
当y=15时,2(x﹣1)2﹣3=15,
解得x=4或x=﹣2,
∵当0≤x≤a时,y的最大值为15,
∴a=4,
故选:D.
9.解:∵x+y2=3,
∴y2=3﹣x,
∵3﹣x≥0,
∴x≤3,
∴s=x2+8y2=x2+8(3﹣x)=x2﹣8x+24=(x﹣4)2+8,
∴s≥9.
故选:D.
10.解:∵s=,
∴s2=4h(20﹣h)=﹣4(h﹣10)2+400,
∴当h为10cm时,射程s有最大值,最大射程是20cm.
设垫高的高度为m,则s2=4h(20+m﹣h)=﹣4(h﹣)2+(20+m)2,
∴当h=cm时,s最大为20+m=20+10,
∴m=10cm,此时h==15cm.
∴小孔离水面的竖直距离为15cm.
故选:B.
二.填空题
11.解:如右图所示,建立平面直角坐标系,
设抛物线的解析式为:y=ax2+3,
∵函数图象过点A(﹣,0),
∴0=a(﹣)2+3,
解得:a=﹣,
∴抛物线的解析式为:y=﹣x2+3,
当y=1时,1=﹣x2+3,
解得:x1=,x2=﹣(舍去),
∴水面的宽度是:米.
故答案为:.
12.解:y=mx2+2mx+1=m(x+1)2﹣m.
当m>0时,
当x=2时,y有最大值,
∴4m+4m+1=4,
∴m=;
当m<0时,
当x=﹣1时,y有最大值,
∴m﹣2m+1=4,
∴m=﹣3,
综上所述:m的值为或﹣3.
故答案是:或﹣3.
13.解:当10≤x≤20时,设y=kx+b,把(10,20),(20,10)代入可得:
,
解得,
∴每天的销售量y(个)与销售价格x(元/个)的函数解析式为y=﹣x+30,
设该食品零售店每天销售这款冷饮产品的利润为w元,
w=(x﹣8)y=(x﹣8)(﹣x+30)=﹣x2+38x﹣240=﹣(x﹣19)2+121,
∵﹣1<0,
∴当x=19时,w有最大值为121,
故答案为:121.
14.解:由图2可知,函数图象的对称轴为x=4,最大值为4,设函数的解析式为y=a(x﹣4)2+4,
将点(0,0)代入得,16a+4=0,
解得:a=﹣,
∴y与x的函数关系式为y=﹣(x﹣4)2+4.
故答案为:y=﹣(x﹣4)2+4.
15.解:以水面所在的直线AB为x轴,以过拱顶C且垂直于AB的直线为y轴建立平面直角坐标系,O为原点,
由题意可得:AO=OB=3米,C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,
把A点坐标(﹣3,0)代入抛物线解析式得,
9a+2=0,
解得:a=﹣,
所以抛物线解析式为y=﹣x2+2,
当x=4时,y=﹣×16+2=﹣,
∴水面下降米,
故答案为:.
16.解:根据题意可知,AB=0.2×8=1.6,以O坐标系的原点,OC所在直线为y轴建立坐标系,如图所示,
设抛物线解析式为y=ax2+bx+c,
∴抛物线过(0.8,0)、(﹣0.8,0)、(﹣0.6,﹣0.28),
∴,
解得.
∴抛物线解析式为y=x2+0.64.
令x=0,则y=0.64.
∴OC=0.64.
故答案为:0.64.
17.解:因为两个抛物线形状相同,可设:yAB=m(x﹣xA)(x﹣xB)①,yCD=m(x﹣xC)(x﹣xD)②,其中xA,xB,xC,xD分别为A,B,C,D的横坐标,
对于①令x=0,则y=mxA xB,
所以E点坐标为(0,mxAxB);
同理,对于②令x=0,则y=mxC xD,
所以E点坐标为(0,mxCxD),
因为mxAxB=mxCxD,即xAxB=xCxD,
因为AB=50米,BC=10米,CD=40米.
所以AC=60米,
所以xC﹣xA=60,xC﹣xB=10,xD﹣xC=40,
所以xA=xC﹣60,xB=xC﹣10,xD=xC十40,
将上式代入xAxB=xCxD得,
(xC60)(xC﹣10)=xC(xC40),
解得xC=,
又因为xB=﹣,
所以=﹣=.
故答案为:.
三.解答题
18.解:(1)x2﹣6x+11=(x﹣3)2+2,
∵(x﹣3)2≥0,
∴(x﹣3)2+2≥2,
∴代数式x2﹣6x+11的最小值为2;
(2)∵a2+2a+1+|b﹣2022|=0,
∴(a+1)2+|b﹣2022|=0,
∴a+1=0,b﹣2022=0,
∴a=﹣1,b=2022,
∴ab=(﹣1)2022=1,
故答案为:1;
(3)设花园的面积为ym2,由题意可得,
y=x(20﹣2x)=﹣2x2+20x=﹣2(x2﹣10x)=﹣2(x﹣5)2+50,
∵﹣2<0,
∴当x=5时,y最大,最大值为50,
此时BC的长是20﹣2×5=10<15,
∴当x=5时,花园的面积最大,最大面积是50m2.
19.解:(1)设一次函数的关系式为y=kx+b,
由题图可知,函数图象过点(25,50)和点(35,30).
把这两点的坐标代入一次函数y=kx+b,
得,
解得,
∴一次函数的关系式为y=﹣2x+100;
(2)根据题意,设当天玩具的销售单价是x元,
由题意得,
(x﹣10)×(﹣2x+100)=600,
解得:x1=40,x2=20,
∴当天玩具的销售单价是40元或20元;
(3)根据题意,则w=(x﹣10)×(﹣2x+100),
整理得:w=﹣2(x﹣30)2+800;
∵﹣2<0,
∴当x=30时,w有最大值,最大值为800;
∴当玩具的销售单价定为30元时,日销售利润最大;最大利润是800元.
20.解:(1)①如图1,由题意得A(2,2)是上边缘抛物线的顶点,
设y=a(x﹣2)2+2,
又∵抛物线过点(0,1.5),
∴1.5=4a+2,
∴a=﹣,
∴上边缘抛物线的函数解析式为y=﹣(x﹣2)2+2,
当y=0时,0=﹣(x﹣2)2+2,
解得x1=6,x2=﹣2(舍去),
∴喷出水的最大射程OC为6m;
②∵对称轴为直线x=2,
∴点(0,1.5)的对称点为(4,1.5),
∴下边缘抛物线是由上边缘抛物线向左平移4m得到的,
∴点B的坐标为(2,0);
③∵EF=0.5,
∴点F的纵坐标为0.5,
∴0.5=﹣(x﹣2)2+2,
解得x=2±2,
∵x>0,
∴x=2+2,
当x>2时,y随x的增大而减小,
∴当2≤x≤6时,要使y≥0.5,
则x≤2+2,
∵当0≤x≤2时,y随x的增大而增大,且x=0时,y=1.5>0.5,
∴当0≤x≤6时,要使y≥0.5,则0≤x≤2+2,
∵DE=3,灌溉车行驶时喷出的水能浇灌到整个绿化带,
∴d的最大值为2+2﹣3=2﹣1,
再看下边缘抛物线,喷出的水能浇灌到绿化带底部的条件是OB≤d,
∴d的最小值为2,
综上所述,d的取值范围是2≤d≤2﹣1;
(2)当喷水口高度最低,且恰好能浇灌到整个绿化带时,点D、F恰好分别在两条抛物线上,
故设点D(m,﹣(m+2)2+h+0.5),F(m+3,﹣[(m+3﹣2)2+h+0.5]),
则有﹣(m+3﹣2)2+h+0.5﹣[﹣(m+2)2+h+0.5]=1,
解得m=2.5,
∴点D的纵坐标为h﹣,
∴h﹣=0,
∴h的最小值为.
同课章节目录
