【核心素养目标】25.3.2 用频率估计概率 课件(共26张PPT)
文档属性
| 名称 | 【核心素养目标】25.3.2 用频率估计概率 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-21 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
25.3.1 用频率估计概率
人教版九年级上册
教学目标
教学目标:1. 用频率估计概率解决实际问题.
2.充分理解用频率估计概率.
教学重点: 用频率估计概率解决实际问题.
教学难点:用频率估计概率解决实际问题.
新知导入
情境引入
知识回顾
对一般的随机事件,在做大量的重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
因此,在以通过大量的重复试验,用一个随机事件发生的频率估计它的概率.
新知讲解
合作学习
问题引入
问题 在生活中你还遇到过哪些用频率估计概率的
实际问题?
.
问题1:某林业部门要考察某种幼树在一定条件下的移植成活率,应采用什么具体做法?
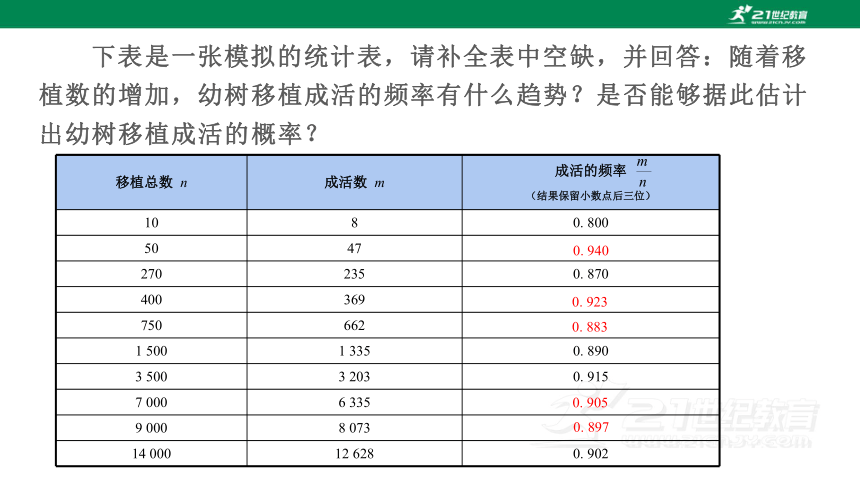
下表是一张模拟的统计表,请补全表中空缺,并回答:随着移植数的增加,幼树移植成活的频率有什么趋势?是否能够据此估计出幼树移植成活的概率?
移植总数 n 成活数 m 成活的频率
(结果保留小数点后三位)
10 8 0. 800
50 47
270 235 0. 870
400 369
750 662
1 500 1 335 0. 890
3 500 3 203 0. 915
7 000 6 335
9 000 8 073
14 000 12 628 0. 902
0. 940
0. 923
0. 883
0. 905
0. 897
从上表可以发现,随着移植数的增加,幼树移植成活的频率越来越稳定,当移植总数 为14 000时,成活的频率为0.902,于是可以估计幼树移植成活的概率为0.9.
解:
在同样的条件下,对这种幼树进行大量移植随着移植数n会越来越大,频率 会越来越 .于是就可以把频率作为 的估计值.
成活率
稳定
提炼概念
典例精讲
问题2 : 某水果公司以2元/千克的成本新进了10 000千克柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.请你帮忙完成此表.
柑橘总质量 n / 千克 损坏柑橘质量 m / 千克 柑橘损坏的频率
(结果保留小数点后三位)
50 5.50 0.110
100 10.50 0.105
150 15.15
200 19.42
250 24.25
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
若柑橘没有损坏,要获得 5 000 元利润应如何定价?
柑橘损坏后,柑橘的重量减少了,为了确保获得
5 000 元利润,定价应如何变化?
如何知道柑橘的重量将减少多少?
思考
分析:用什么办法估计柑橘的损坏率?
随着统计的频率越来越稳定,柑橘的损坏率为 0.1,
则柑橘的完好概率为 0.9.
设每千克柑橘的售价为x 元,
根据“利润=(售价-实际成本) 完好的质量”列方程求解.
解:销售人员已经对柑橘损坏率进行了抽样统计,填完表格后可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为 500 kg 时的损坏频率为 0.103,于是可以估计柑橘损坏的概率约为 0.1(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
根据估计的概率可以知道,在10000kg柑橘中完好柑橘的质量为10000×0.9=9000(kg),完好柑橘的实际成本为
设每千克柑橘的售价为x元,则应有
(x-2.22)×9 000=5 000
解得 x≈2.8(元)
因此,出售柑橘时,每千克定价大约2.8元可获利润5000元.
归纳概念
在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性.概率是频率的稳定值,而频率是概率的近似值.
课堂练习
1. 某林业局将一种树苗移植成活的情况绘制成如下统计图,由此可估计这种树苗移植成活的概率约为( )
A. 0.95 B. 0.90
C. 0.85 D. 0.80
B
2.一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有4个,若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a大约是( )
A.25 B.20 C.15 D.10
B
3. 植树节过后,历下区园林绿化管理局为了考察树苗的成活率,于是进行了现场统计,表中记录了树苗的成活情况,则由此估计这种树苗成活的概率约为 (结果精确到0.1) .
0.9
植树总数 400 1500 3500 7000 9000 14000
成活数 369 1335 3203 6335 8073 12628
成活的频率 0.923 0.890 0.915 0.905 0.897 0.902
试验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m 1 4 45 92 188 476 951 1900 2850
发芽频率 1 0.80 0.90 0.92 0.94 0.952 0.951 a b
(1)计算表中a、b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则有多少千克的麦种可以成活为秧苗?
4.在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
解:(1)a=1900÷2000=0.95,b=2850÷3000=0.95.
(2)观察发现,随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,所以该麦种的发芽概率约为0.95.
(3)100×0.95×87%=82.65(千克),故有82.65千克的麦种可以成活为秧苗.
5. 4件同型号的产品中,有1件不合格品和3件合格品.在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,由此可以推算出 x 的值大约是多少?
解得
经检验, x=16是分式方程的解.
答:x的值大约是16.
解:由题意,得
课堂总结
用频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
25.3.1 用频率估计概率
人教版九年级上册
教学目标
教学目标:1. 用频率估计概率解决实际问题.
2.充分理解用频率估计概率.
教学重点: 用频率估计概率解决实际问题.
教学难点:用频率估计概率解决实际问题.
新知导入
情境引入
知识回顾
对一般的随机事件,在做大量的重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.
因此,在以通过大量的重复试验,用一个随机事件发生的频率估计它的概率.
新知讲解
合作学习
问题引入
问题 在生活中你还遇到过哪些用频率估计概率的
实际问题?
.
问题1:某林业部门要考察某种幼树在一定条件下的移植成活率,应采用什么具体做法?
下表是一张模拟的统计表,请补全表中空缺,并回答:随着移植数的增加,幼树移植成活的频率有什么趋势?是否能够据此估计出幼树移植成活的概率?
移植总数 n 成活数 m 成活的频率
(结果保留小数点后三位)
10 8 0. 800
50 47
270 235 0. 870
400 369
750 662
1 500 1 335 0. 890
3 500 3 203 0. 915
7 000 6 335
9 000 8 073
14 000 12 628 0. 902
0. 940
0. 923
0. 883
0. 905
0. 897
从上表可以发现,随着移植数的增加,幼树移植成活的频率越来越稳定,当移植总数 为14 000时,成活的频率为0.902,于是可以估计幼树移植成活的概率为0.9.
解:
在同样的条件下,对这种幼树进行大量移植随着移植数n会越来越大,频率 会越来越 .于是就可以把频率作为 的估计值.
成活率
稳定
提炼概念
典例精讲
问题2 : 某水果公司以2元/千克的成本新进了10 000千克柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在下表中.请你帮忙完成此表.
柑橘总质量 n / 千克 损坏柑橘质量 m / 千克 柑橘损坏的频率
(结果保留小数点后三位)
50 5.50 0.110
100 10.50 0.105
150 15.15
200 19.42
250 24.25
300 30.93
350 35.32
400 39.24
450 44.57
500 51.54
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
若柑橘没有损坏,要获得 5 000 元利润应如何定价?
柑橘损坏后,柑橘的重量减少了,为了确保获得
5 000 元利润,定价应如何变化?
如何知道柑橘的重量将减少多少?
思考
分析:用什么办法估计柑橘的损坏率?
随着统计的频率越来越稳定,柑橘的损坏率为 0.1,
则柑橘的完好概率为 0.9.
设每千克柑橘的售价为x 元,
根据“利润=(售价-实际成本) 完好的质量”列方程求解.
解:销售人员已经对柑橘损坏率进行了抽样统计,填完表格后可以看出,随着柑橘质量的增加,柑橘损坏的频率越来越稳定.柑橘总质量为 500 kg 时的损坏频率为 0.103,于是可以估计柑橘损坏的概率约为 0.1(结果保留小数点后一位).由此可知,柑橘完好的概率为0.9.
根据估计的概率可以知道,在10000kg柑橘中完好柑橘的质量为10000×0.9=9000(kg),完好柑橘的实际成本为
设每千克柑橘的售价为x元,则应有
(x-2.22)×9 000=5 000
解得 x≈2.8(元)
因此,出售柑橘时,每千克定价大约2.8元可获利润5000元.
归纳概念
在大量的重复试验中,随机事件发生的频率会呈现出明显的规律性:随着试验次数的增加,频率将会越来越集中在一个常数附近,具有稳定性.概率是频率的稳定值,而频率是概率的近似值.
课堂练习
1. 某林业局将一种树苗移植成活的情况绘制成如下统计图,由此可估计这种树苗移植成活的概率约为( )
A. 0.95 B. 0.90
C. 0.85 D. 0.80
B
2.一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有4个,若每次将球搅匀后,任意摸出1个球记下颜色再放回暗箱,通过大量重复摸球实验后发现,摸到红球的频率稳定在20%附近,那么可以推算出a大约是( )
A.25 B.20 C.15 D.10
B
3. 植树节过后,历下区园林绿化管理局为了考察树苗的成活率,于是进行了现场统计,表中记录了树苗的成活情况,则由此估计这种树苗成活的概率约为 (结果精确到0.1) .
0.9
植树总数 400 1500 3500 7000 9000 14000
成活数 369 1335 3203 6335 8073 12628
成活的频率 0.923 0.890 0.915 0.905 0.897 0.902
试验种子n(粒) 1 5 50 100 200 500 1000 2000 3000
发芽频数m 1 4 45 92 188 476 951 1900 2850
发芽频率 1 0.80 0.90 0.92 0.94 0.952 0.951 a b
(1)计算表中a、b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则有多少千克的麦种可以成活为秧苗?
4.在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
解:(1)a=1900÷2000=0.95,b=2850÷3000=0.95.
(2)观察发现,随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,所以该麦种的发芽概率约为0.95.
(3)100×0.95×87%=82.65(千克),故有82.65千克的麦种可以成活为秧苗.
5. 4件同型号的产品中,有1件不合格品和3件合格品.在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,由此可以推算出 x 的值大约是多少?
解得
经检验, x=16是分式方程的解.
答:x的值大约是16.
解:由题意,得
课堂总结
用频率估计概率
大量重复试验
求非等可能性事件概率
列举法
不能适应
频率稳定
常数附近
统计思想
用样本(频率)估计总体(概率)
一种关系
频率与概率的关系
频率稳定时可看作是概
率但概率与频率无关
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
