人教版数学四年级上册单元测试卷第三单元 角的度量(含答案)
文档属性
| 名称 | 人教版数学四年级上册单元测试卷第三单元 角的度量(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 15:30:27 | ||
图片预览




文档简介
人教版数学四年级上册单元测试卷
第三单元 角的度量
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 七 总分
得分
一、选择题
1.陈叔叔在跑道上画了一条长10米的( )。
A.线段 B.射线 C.直线
2.下图中共有( )条线段。
A.8 B.9 C.10 D.11
3.下列说法错误的是( )。
A.直线没有端点
B.当两条直线相交成直角时,这两条直线就互相垂直
C.91°的角是锐角
D.1个周角的大小等于2个平角
4.一个平角减去一个钝角,结果一定是( )。
A.锐角 B.直角 C.钝角 D.不能确定
5.3点30分时,钟面上时针和分针组成的角是( )。
A.锐角 B.钝角 C.直角 D.平角
二、图形计算
6.下面是用三角尺拼成的图形,想一想图中所标的角各是多少度?
∠1=( )
∠2=( )
∠3=( )
∠4=( )
7.已知∠1=50°,求∠2和∠3的度数。
三、口算和估算
8.脱口秀
180°﹣25°﹣75°= 180°﹣(37°+63°)= 90°﹣37°=
80°+36°+64°= 178°﹣(78°+54°)= 180°﹣85°=
四、填空题
9.从一点引出两条( )组成的图形叫做角,这个点叫做角的( )。量角的大小,要用( );角的度量单位是( )。
10.直线________端点,射线有________个端点,线段有________个端点。
11.在时钟上,时针与分针成90°是( )时与( )时;时针和分针形成平角的时刻是( )。
12.在连结两点的所有线中,( )最短。
13.用量角器量角时,把量角器的中心与角的( )重合,0°刻度线与角的( )重合,则另一条边所对的量角器上的刻度,就是这个角的大小.
14.一长方形纸片,按如下图所示的方式折叠,BC,BD为折痕。若∠ABC=30°,则∠EBD的度数是( )。
15.在下面图形中,( )是直线,( )是射线,( )是线段。
16.如图,∠1=23°,∠2=________°,∠3=________°。
17.过两点能画( )条直线,过一点可以画( )条直线。
18.1周角=( )平角=( )直角。
五、判断题
19.如果把一个角的两条边延长,这个角就变大了。( )
20.线段是直线上两点之间的部分。( )
21.一条直线就是平角。 ( )
22.直线的长度是射线的两倍。( )
23.大于90°的角是钝角。( )
六、作图题
24.量一量,画一圆.
(1)量出下图中∠1的度数.
∠1=( )°
(2)以O为顶点,射线OA为一条边,画出∠2,使∠2的度数是125°.
七、解答题
25.甲角是乙角的3倍,甲、乙两角的和是136°,求乙角有多少度?
26.某果园种了352棵梨树和492棵苹果树,如果每年大约每棵梨树可收梨93千克,每棵苹果树可收苹果102千克,这个果园一年可收梨和苹果共多少千克?
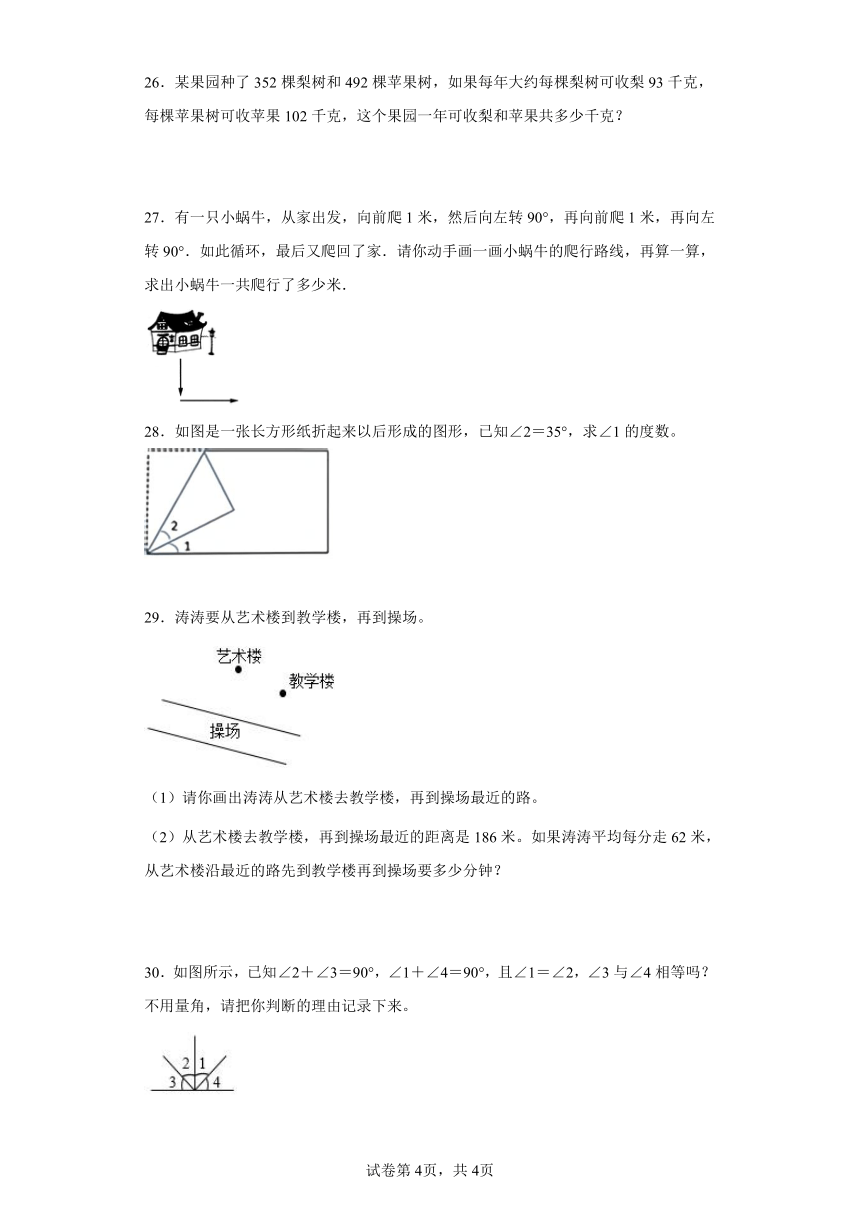
27.有一只小蜗牛,从家出发,向前爬1米,然后向左转90°,再向前爬1米,再向左转90°.如此循环,最后又爬回了家.请你动手画一画小蜗牛的爬行路线,再算一算,求出小蜗牛一共爬行了多少米.
28.如图是一张长方形纸折起来以后形成的图形,已知∠2=35°,求∠1的度数。
29.涛涛要从艺术楼到教学楼,再到操场。
(1)请你画出涛涛从艺术楼去教学楼,再到操场最近的路。
(2)从艺术楼去教学楼,再到操场最近的距离是186米。如果涛涛平均每分走62米,从艺术楼沿最近的路先到教学楼再到操场要多少分钟?
30.如图所示,已知∠2+∠3=90°,∠1+∠4=90°,且∠1=∠2,∠3与∠4相等吗?不用量角,请把你判断的理由记录下来。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
直线和射线是无限长,没有长度;线段是有限的,所以陈叔叔在跑道上画了一条长10米的线段。
故答案为:A
2.C
【解析】
【详解】
单个的线段4条,两条线段组成的线段3条,三条线段组成的线段2条,四条线段组成的线段1条,共4+3+2+1=10(条)
故答案为A
3.C
【解析】
【分析】
直线:一点在空间沿着一个方向及它的相反方向运动,所形成的图形是直线;
垂线:两条直线相交成直角时,这两条直线互相垂直;
锐角:小于90°大于0°的角;
周角:等于360°的角;平角:等于180°的角。
【详解】
A:直线没有端点,正确;
B:由垂直定义可知,正确;
C:由锐角的定义可知,错误;
D:360°=180°×2,正确。
故答案为C。
【点睛】
直线、射线、线段的判定是一个难点。这是因为,很难在生活中找到直线的例子,而一些光线大多可以看做射线,线段的例子较多,如拉直的一根线,一张纸的边等。
4.A
【解析】
【分析】
根据平角和钝角的定义可知:平角=180°,90°<钝角<180°,可得一个平角减去一个钝角后的角大于0°,小于90°,它是一个锐角,据此解答即可。
【详解】
据分析得出:
一个平角减去一个钝角,结果一定是锐角。
故答案为:A
【点睛】
此题主要考查角的概念及分类,弄清楚各类角的度数即可判断。
5.A
【解析】
【分析】
根据钟面平均分成12份,可得每份的度数,根据每份的度数乘时针与分针相距的份数,可得答案。
【详解】
3点30分时,它的时针和分针所成的角是30°×2.5=75°。
故答案为:A
【点睛】
本题考查了钟面角,每份的度数乘时针与分针相距的份数是解题关键。
6. 135° 150° 15° 60°
【解析】
【分析】
(1)用平角减去45°的角;
(2)用平角减去30°的角;
(3)用45°减去30°的角;
(4)用90°减去30°的角。
【详解】
(1)∠1=180°﹣45°=135°
(2)∠2=180°﹣30°=150°
(3)∠3=45°﹣30°=15°
(4)∠5=90°﹣30°=60°
故答案为:。
【点评】
考查了角的计算,关键是熟悉三角板上角的度数。
7.∠2=40°
∠3=140°
【解析】
【分析】
本题考查直角与平角的认识,根据题意可知,∠1+∠2=90°,∠2+∠3=180°,据此解答。
【详解】
∠2=90°-∠1
=90°-50°
=40°
∠3=180°-∠2
=180°-40°
=140°
8.80°;80°;53°
180°;46°;95°
【解析】
【分析】
整数四则混合运算法则,先算乘除后算加减,有括号先算括号里面的。整数加减法运算,数位对齐,依照从低到高的顺序依次加减即可。注意最后在结果后面加上单位“度”。
【详解】
180°﹣25°﹣75°=155°-75°=80°
180°﹣(37°+63°)=180°﹣100°=80°
90°﹣37°=53°
80°+36°+64°=116°+64°=180°
178°﹣(78°+54°)=178°-132°=46°
180°﹣85°=95°
【点睛】
运用整数加减运算的运算法则解答,最后在结果后面加上单位°即可。
9. 射线 顶点 量角器 度
【解析】
略
10. 没有 1 2
【解析】
【详解】
线的基本概念。直线没有端点,射线有1个端点,线段有2个端点。
11. 3 9 6时
【解析】
【详解】
略。
12.线段
【解析】
略
13. 顶点 一边
【解析】
【分析】
量角器测量角时,量角器的中心和角的顶点重合,0刻度线和角的一边重合,另一边所指的刻度就是角的大小.
【详解】
解:用量角器测量角时,量角器的中心和角的顶点重合,0刻度线和角的一边重合,另一边所指的刻度就是角的大小.故答案为顶点;一边.
14.60°
【解析】
因为折叠前后的角度相等,所以∠ABC=∠A′BC,∠EBD=∠E′BD,所以∠EBD和∠E′BD的度数用180°去掉2个30°再除以2即可求解。
【详解】
∠EBD=(180°-30°×2)÷2=60°
【点睛】
解答本题的关键是熟练掌握折叠的性质:折叠前后对应线段相等,对应角相等。
15. ②⑦ ①⑥ ③
【解析】
【详解】
直线没有端点,射线有1个端点,线段有2个端点.而且都是直的,没有曲的.
②⑦是直线,①⑥是射线,③是线段
考点:直线、射线、线段的定义.
16. 67° 113°
【解析】
【分析】
由图可知,∠1与∠2组成直角,直角等于90°,故∠2=90°-∠1
∠3与∠2组成平角,平角等于180°,故∠3=180°-∠2
据此解答即可。
【详解】
∠2=90°-∠1=90°-23°=67°
∠3=180°-∠2=180°-67°=113°
故答案为:67°;113°
【点睛】
此题考查角的度量,需要学会区分直角以及平角,还要掌握其度数特点。
17. 1 无数
【解析】
【详解】
过两点能画1条直线,过一点可以画无数条直线。如图所示:
18. 2 4
【解析】
【分析】
360°的角叫做周角,180°的角叫做平角,90°的角叫做直角,360°=2×180°=4×90°。据此解答即可。
【详解】
1周角=2平角=4直角。
【点睛】
熟练掌握周角、平角和直角的定义是解决本题的关键。
19.×
【解析】
【分析】
根据角的含义:由一点引出的两条射线所组成的图形叫做角;可知角的大小只与角的两边叉开的大小有关,和两边的长短无关,一个角的两边无论怎么延长,角的大小不变。
【详解】
由分析可知,角的大小与两边的长短无关,故答案为:×。
【点睛】
此题考查了角的含义,应明确:角的大小只与角的两边叉开的大小有关和两边的长短无关。
20.√
【解析】
【详解】
略
21.×
【解析】
【详解】
略
22.×
【解析】
【分析】
把线段的两端无限延长,得到一条直线,直线没有端点,无限长。把线段的一端无限延长,得到一条射线,射线有一个端点,无限长。据此判断即可。
【详解】
直线和射线均是无限长的,则“直线的长度是射线的两倍”这种说法是错误的。
故答案为:×。
【点睛】
本题考查直线、射线的性质,直线和射线是无限长的,只有线段是有限长的。
23.×
【解析】
【分析】
由题意可得大于90°小于180°的角叫做钝角,180°的角叫做平角,360°的角叫做周角,据此解答即可。
【详解】
大于90°的角不一定是钝角,还有可能是平角或者周角;且大于90°小于180°的角叫做钝角,故此说法错误。
【点睛】
本题考查钝角的定义,钝角不仅要大于90°,还要小于180°。
24.(1)30
(2)
【解析】
【详解】
略
25.34°
【解析】
略
26.82920千克
【解析】
【分析】
考察计算器的用法,先根据题意列出解题式子352×93+492×102,再在计算器上输入式子后得出正确答案,注意数据和运算符号不能输错
【详解】
依题意,这个果园一年可收的梨的斤数为352×93千克,可收的苹果的斤数为492×102千克,则可列出解题式子:352×93+492×102,在计算器输入数字和运算符号后,可得结果是82920.
352×93+492×102=82920(千克)
答:这个果园一年可收梨和苹果共82920千克.
27.4米
【解析】
【详解】
1×4=4(米)
如图便可知:
28.20°
【解析】
【分析】
如图,把这张纸展开后,以∠1、∠2的顶点为顶点的角是90°,由于∠2盖住了一个和它相等的角,展开后就是∠1+2∠2=90°,又知∠2=35°,据此可求出∠1的度数。
【详解】
90°﹣35°×2
=90°﹣70°
=20°
答:∠1的度数是20°。
【点评】
本题是考查简单图形的折叠问题及角度的计算。关键是∠2盖住了一个和它相等的角。
29.(1)
(2)3分钟
【解析】
【分析】
(1)两点之间线段最短,点到直线之间的距离最短,据此画出最短路线即可;
(2)根据时间=路程÷速度,求出所需时间即可。
【详解】
(1)如图所示:;
(2)186÷62=3(分钟)
答:从艺术楼沿最近的路先到教学楼再到操场要3分钟。
故答案为:(1)
(2)3分钟
【点睛】
本题考查两点之间线段最短、点到直线之间的距离和行程问题,解答本题的关键是掌握应用两点之间线段最短、点到直线之间的距离最短解决实际问题。
30.∠3与∠4相等。因为∠3=90°-∠2,∠4=90°-∠1,∠1=∠2,所以∠3与∠4相等。
【解析】
【分析】
如果两个角的和等于90°,就说这两角互为余角,简称互余,等角的余角相等,据此解答。
【详解】
因为∠3=90°-∠2,∠4=90°-∠1,∠1=∠2,所以∠3与∠4相等。
【点睛】
本题考查了两角大小关系的判断,掌握等角的余角相等是解题的关键。
答案第1页,共2页
答案第1页,共2页
第三单元 角的度量
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 六 七 总分
得分
一、选择题
1.陈叔叔在跑道上画了一条长10米的( )。
A.线段 B.射线 C.直线
2.下图中共有( )条线段。
A.8 B.9 C.10 D.11
3.下列说法错误的是( )。
A.直线没有端点
B.当两条直线相交成直角时,这两条直线就互相垂直
C.91°的角是锐角
D.1个周角的大小等于2个平角
4.一个平角减去一个钝角,结果一定是( )。
A.锐角 B.直角 C.钝角 D.不能确定
5.3点30分时,钟面上时针和分针组成的角是( )。
A.锐角 B.钝角 C.直角 D.平角
二、图形计算
6.下面是用三角尺拼成的图形,想一想图中所标的角各是多少度?
∠1=( )
∠2=( )
∠3=( )
∠4=( )
7.已知∠1=50°,求∠2和∠3的度数。
三、口算和估算
8.脱口秀
180°﹣25°﹣75°= 180°﹣(37°+63°)= 90°﹣37°=
80°+36°+64°= 178°﹣(78°+54°)= 180°﹣85°=
四、填空题
9.从一点引出两条( )组成的图形叫做角,这个点叫做角的( )。量角的大小,要用( );角的度量单位是( )。
10.直线________端点,射线有________个端点,线段有________个端点。
11.在时钟上,时针与分针成90°是( )时与( )时;时针和分针形成平角的时刻是( )。
12.在连结两点的所有线中,( )最短。
13.用量角器量角时,把量角器的中心与角的( )重合,0°刻度线与角的( )重合,则另一条边所对的量角器上的刻度,就是这个角的大小.
14.一长方形纸片,按如下图所示的方式折叠,BC,BD为折痕。若∠ABC=30°,则∠EBD的度数是( )。
15.在下面图形中,( )是直线,( )是射线,( )是线段。
16.如图,∠1=23°,∠2=________°,∠3=________°。
17.过两点能画( )条直线,过一点可以画( )条直线。
18.1周角=( )平角=( )直角。
五、判断题
19.如果把一个角的两条边延长,这个角就变大了。( )
20.线段是直线上两点之间的部分。( )
21.一条直线就是平角。 ( )
22.直线的长度是射线的两倍。( )
23.大于90°的角是钝角。( )
六、作图题
24.量一量,画一圆.
(1)量出下图中∠1的度数.
∠1=( )°
(2)以O为顶点,射线OA为一条边,画出∠2,使∠2的度数是125°.
七、解答题
25.甲角是乙角的3倍,甲、乙两角的和是136°,求乙角有多少度?
26.某果园种了352棵梨树和492棵苹果树,如果每年大约每棵梨树可收梨93千克,每棵苹果树可收苹果102千克,这个果园一年可收梨和苹果共多少千克?
27.有一只小蜗牛,从家出发,向前爬1米,然后向左转90°,再向前爬1米,再向左转90°.如此循环,最后又爬回了家.请你动手画一画小蜗牛的爬行路线,再算一算,求出小蜗牛一共爬行了多少米.
28.如图是一张长方形纸折起来以后形成的图形,已知∠2=35°,求∠1的度数。
29.涛涛要从艺术楼到教学楼,再到操场。
(1)请你画出涛涛从艺术楼去教学楼,再到操场最近的路。
(2)从艺术楼去教学楼,再到操场最近的距离是186米。如果涛涛平均每分走62米,从艺术楼沿最近的路先到教学楼再到操场要多少分钟?
30.如图所示,已知∠2+∠3=90°,∠1+∠4=90°,且∠1=∠2,∠3与∠4相等吗?不用量角,请把你判断的理由记录下来。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
【详解】
直线和射线是无限长,没有长度;线段是有限的,所以陈叔叔在跑道上画了一条长10米的线段。
故答案为:A
2.C
【解析】
【详解】
单个的线段4条,两条线段组成的线段3条,三条线段组成的线段2条,四条线段组成的线段1条,共4+3+2+1=10(条)
故答案为A
3.C
【解析】
【分析】
直线:一点在空间沿着一个方向及它的相反方向运动,所形成的图形是直线;
垂线:两条直线相交成直角时,这两条直线互相垂直;
锐角:小于90°大于0°的角;
周角:等于360°的角;平角:等于180°的角。
【详解】
A:直线没有端点,正确;
B:由垂直定义可知,正确;
C:由锐角的定义可知,错误;
D:360°=180°×2,正确。
故答案为C。
【点睛】
直线、射线、线段的判定是一个难点。这是因为,很难在生活中找到直线的例子,而一些光线大多可以看做射线,线段的例子较多,如拉直的一根线,一张纸的边等。
4.A
【解析】
【分析】
根据平角和钝角的定义可知:平角=180°,90°<钝角<180°,可得一个平角减去一个钝角后的角大于0°,小于90°,它是一个锐角,据此解答即可。
【详解】
据分析得出:
一个平角减去一个钝角,结果一定是锐角。
故答案为:A
【点睛】
此题主要考查角的概念及分类,弄清楚各类角的度数即可判断。
5.A
【解析】
【分析】
根据钟面平均分成12份,可得每份的度数,根据每份的度数乘时针与分针相距的份数,可得答案。
【详解】
3点30分时,它的时针和分针所成的角是30°×2.5=75°。
故答案为:A
【点睛】
本题考查了钟面角,每份的度数乘时针与分针相距的份数是解题关键。
6. 135° 150° 15° 60°
【解析】
【分析】
(1)用平角减去45°的角;
(2)用平角减去30°的角;
(3)用45°减去30°的角;
(4)用90°减去30°的角。
【详解】
(1)∠1=180°﹣45°=135°
(2)∠2=180°﹣30°=150°
(3)∠3=45°﹣30°=15°
(4)∠5=90°﹣30°=60°
故答案为:。
【点评】
考查了角的计算,关键是熟悉三角板上角的度数。
7.∠2=40°
∠3=140°
【解析】
【分析】
本题考查直角与平角的认识,根据题意可知,∠1+∠2=90°,∠2+∠3=180°,据此解答。
【详解】
∠2=90°-∠1
=90°-50°
=40°
∠3=180°-∠2
=180°-40°
=140°
8.80°;80°;53°
180°;46°;95°
【解析】
【分析】
整数四则混合运算法则,先算乘除后算加减,有括号先算括号里面的。整数加减法运算,数位对齐,依照从低到高的顺序依次加减即可。注意最后在结果后面加上单位“度”。
【详解】
180°﹣25°﹣75°=155°-75°=80°
180°﹣(37°+63°)=180°﹣100°=80°
90°﹣37°=53°
80°+36°+64°=116°+64°=180°
178°﹣(78°+54°)=178°-132°=46°
180°﹣85°=95°
【点睛】
运用整数加减运算的运算法则解答,最后在结果后面加上单位°即可。
9. 射线 顶点 量角器 度
【解析】
略
10. 没有 1 2
【解析】
【详解】
线的基本概念。直线没有端点,射线有1个端点,线段有2个端点。
11. 3 9 6时
【解析】
【详解】
略。
12.线段
【解析】
略
13. 顶点 一边
【解析】
【分析】
量角器测量角时,量角器的中心和角的顶点重合,0刻度线和角的一边重合,另一边所指的刻度就是角的大小.
【详解】
解:用量角器测量角时,量角器的中心和角的顶点重合,0刻度线和角的一边重合,另一边所指的刻度就是角的大小.故答案为顶点;一边.
14.60°
【解析】
因为折叠前后的角度相等,所以∠ABC=∠A′BC,∠EBD=∠E′BD,所以∠EBD和∠E′BD的度数用180°去掉2个30°再除以2即可求解。
【详解】
∠EBD=(180°-30°×2)÷2=60°
【点睛】
解答本题的关键是熟练掌握折叠的性质:折叠前后对应线段相等,对应角相等。
15. ②⑦ ①⑥ ③
【解析】
【详解】
直线没有端点,射线有1个端点,线段有2个端点.而且都是直的,没有曲的.
②⑦是直线,①⑥是射线,③是线段
考点:直线、射线、线段的定义.
16. 67° 113°
【解析】
【分析】
由图可知,∠1与∠2组成直角,直角等于90°,故∠2=90°-∠1
∠3与∠2组成平角,平角等于180°,故∠3=180°-∠2
据此解答即可。
【详解】
∠2=90°-∠1=90°-23°=67°
∠3=180°-∠2=180°-67°=113°
故答案为:67°;113°
【点睛】
此题考查角的度量,需要学会区分直角以及平角,还要掌握其度数特点。
17. 1 无数
【解析】
【详解】
过两点能画1条直线,过一点可以画无数条直线。如图所示:
18. 2 4
【解析】
【分析】
360°的角叫做周角,180°的角叫做平角,90°的角叫做直角,360°=2×180°=4×90°。据此解答即可。
【详解】
1周角=2平角=4直角。
【点睛】
熟练掌握周角、平角和直角的定义是解决本题的关键。
19.×
【解析】
【分析】
根据角的含义:由一点引出的两条射线所组成的图形叫做角;可知角的大小只与角的两边叉开的大小有关,和两边的长短无关,一个角的两边无论怎么延长,角的大小不变。
【详解】
由分析可知,角的大小与两边的长短无关,故答案为:×。
【点睛】
此题考查了角的含义,应明确:角的大小只与角的两边叉开的大小有关和两边的长短无关。
20.√
【解析】
【详解】
略
21.×
【解析】
【详解】
略
22.×
【解析】
【分析】
把线段的两端无限延长,得到一条直线,直线没有端点,无限长。把线段的一端无限延长,得到一条射线,射线有一个端点,无限长。据此判断即可。
【详解】
直线和射线均是无限长的,则“直线的长度是射线的两倍”这种说法是错误的。
故答案为:×。
【点睛】
本题考查直线、射线的性质,直线和射线是无限长的,只有线段是有限长的。
23.×
【解析】
【分析】
由题意可得大于90°小于180°的角叫做钝角,180°的角叫做平角,360°的角叫做周角,据此解答即可。
【详解】
大于90°的角不一定是钝角,还有可能是平角或者周角;且大于90°小于180°的角叫做钝角,故此说法错误。
【点睛】
本题考查钝角的定义,钝角不仅要大于90°,还要小于180°。
24.(1)30
(2)
【解析】
【详解】
略
25.34°
【解析】
略
26.82920千克
【解析】
【分析】
考察计算器的用法,先根据题意列出解题式子352×93+492×102,再在计算器上输入式子后得出正确答案,注意数据和运算符号不能输错
【详解】
依题意,这个果园一年可收的梨的斤数为352×93千克,可收的苹果的斤数为492×102千克,则可列出解题式子:352×93+492×102,在计算器输入数字和运算符号后,可得结果是82920.
352×93+492×102=82920(千克)
答:这个果园一年可收梨和苹果共82920千克.
27.4米
【解析】
【详解】
1×4=4(米)
如图便可知:
28.20°
【解析】
【分析】
如图,把这张纸展开后,以∠1、∠2的顶点为顶点的角是90°,由于∠2盖住了一个和它相等的角,展开后就是∠1+2∠2=90°,又知∠2=35°,据此可求出∠1的度数。
【详解】
90°﹣35°×2
=90°﹣70°
=20°
答:∠1的度数是20°。
【点评】
本题是考查简单图形的折叠问题及角度的计算。关键是∠2盖住了一个和它相等的角。
29.(1)
(2)3分钟
【解析】
【分析】
(1)两点之间线段最短,点到直线之间的距离最短,据此画出最短路线即可;
(2)根据时间=路程÷速度,求出所需时间即可。
【详解】
(1)如图所示:;
(2)186÷62=3(分钟)
答:从艺术楼沿最近的路先到教学楼再到操场要3分钟。
故答案为:(1)
(2)3分钟
【点睛】
本题考查两点之间线段最短、点到直线之间的距离和行程问题,解答本题的关键是掌握应用两点之间线段最短、点到直线之间的距离最短解决实际问题。
30.∠3与∠4相等。因为∠3=90°-∠2,∠4=90°-∠1,∠1=∠2,所以∠3与∠4相等。
【解析】
【分析】
如果两个角的和等于90°,就说这两角互为余角,简称互余,等角的余角相等,据此解答。
【详解】
因为∠3=90°-∠2,∠4=90°-∠1,∠1=∠2,所以∠3与∠4相等。
【点睛】
本题考查了两角大小关系的判断,掌握等角的余角相等是解题的关键。
答案第1页,共2页
答案第1页,共2页
