数学人教A版(2019)选择性必修第一册1.1.1 空间向量及其线性运算 课件(共20张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.1 空间向量及其线性运算 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 741.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 08:25:29 | ||
图片预览




文档简介
(共20张PPT)
1.1.1 空间向量及其运算
高中数学
选择性必修
空间向量
空间向量的基本概念(重点)
空间向量的线性运算(重点)
1
2
共线、共面定理
3
空间向量的基本概念
01
一.空间向量的概念
章前图展示的是一个做滑翔伞运动的场景.
在滑翔过程中,飞行员会受到来自不同方向、大小各异的力,例如绳索的拉力、风力、重力等,显然,这些力不在同一个平面内.
平面向量
空间向量
类比的方法
平面向量
一.空间向量的概念
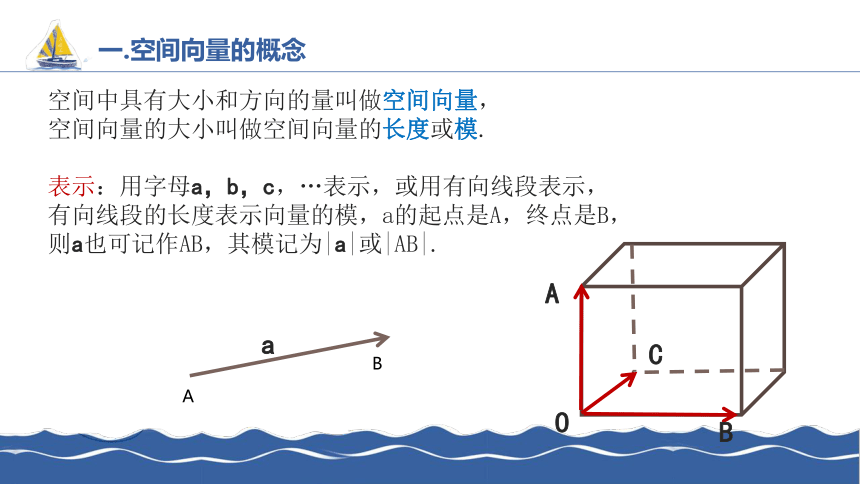
空间中具有大小和方向的量叫做空间向量,
空间向量的大小叫做空间向量的长度或模.
表示:用字母a,b,c,…表示,或用有向线段表示,
有向线段的长度表示向量的模,a的起点是A,终点是B,
则a也可记作AB,其模记为|a|或|AB|.
A
B
a
O
C
A
B
一.空间向量的概念
O
C
A
B
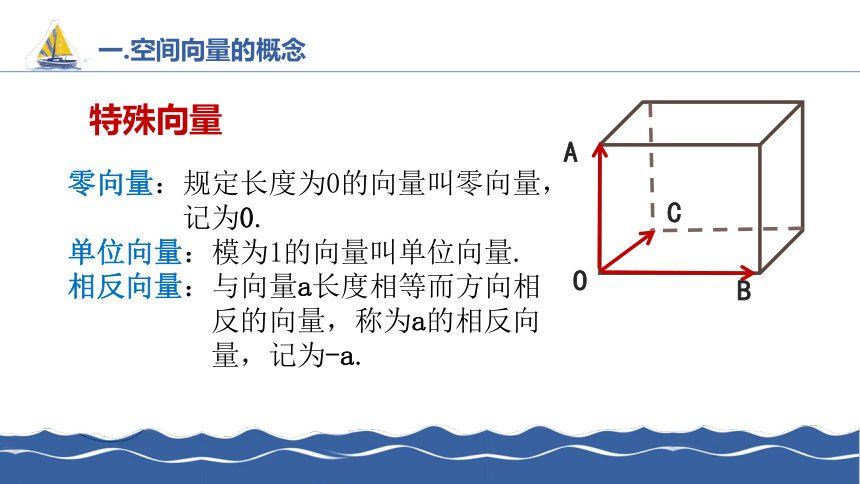
零向量:规定长度为0的向量叫零向量,
记为0.
单位向量:模为1的向量叫单位向量.
相反向量:与向量a长度相等而方向相
反的向量,称为a的相反向
量,记为-a.
特殊向量
一.空间向量的概念
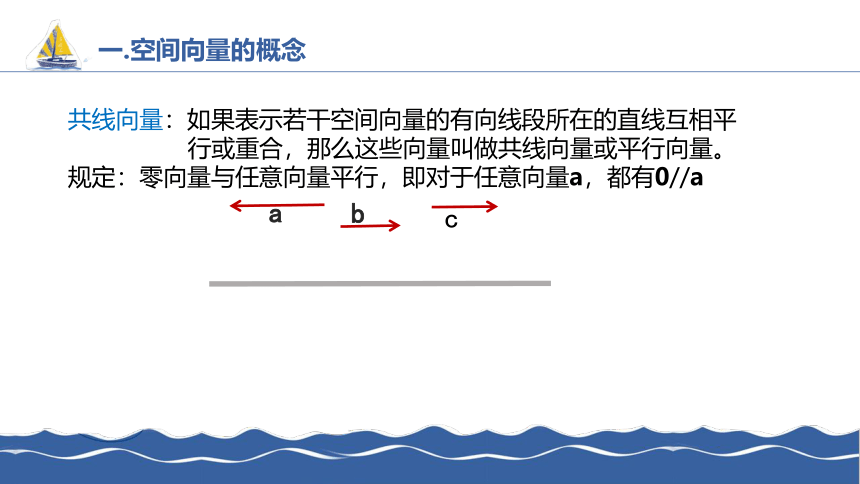
共线向量:如果表示若干空间向量的有向线段所在的直线互相平
行或重合,那么这些向量叫做共线向量或平行向量。
规定:零向量与任意向量平行,即对于任意向量a,都有0//a
a
b
c
一.空间向量的概念
相等向量:方向相同且模相等的向量称为相等向量,
同向且等长的有向线段表示同一向量或相等向量.
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合.因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空问向量都可以平移到同一个平面内,成为同一平面内的两个向量。
如图,已知空间向量a,b,以任意点O为起点,作向量OA=a,OB=b,我们就可以把它们平移到同一个平面a内.
a
b
a
b
O
A
B
b
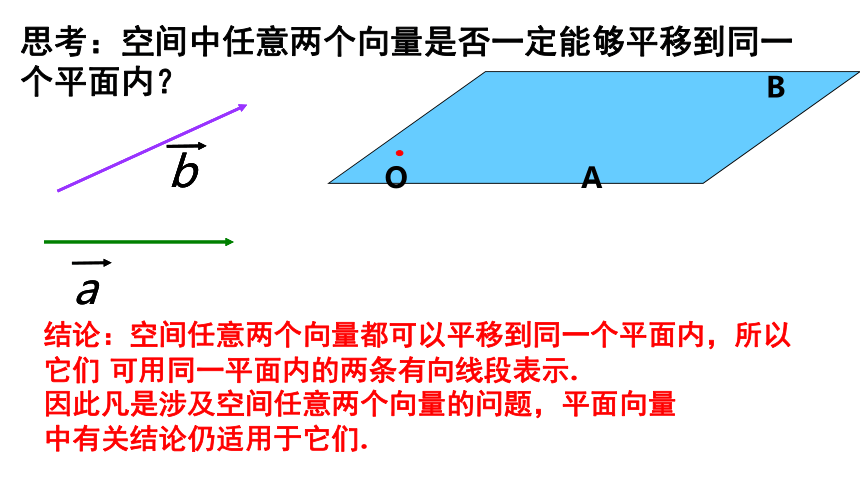
结论:空间任意两个向量都可以平移到同一个平面内,所以它们 可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量
中有关结论仍适用于它们.
思考:空间中任意两个向量是否一定能够平移到同一个平面内?
一.空间向量的概念
空间向量的线性运算
02
加减运算
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(1)空间向量加法运算:
平行四边形法则:
三角形法则:
注:首尾顺次相接,起点指向终点
二.空间向量的线性运算
三角形法则推广
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(2)空间向量的减法运算:
注:起点相同,差向量为减向量终点指向被减向量的终点
二.空间向量的线性运算
二.空间向量的线性运算
数乘运算
向量的加、减、数乘运算统称向量的线性运算.
二.空间向量的线性运算
二.空间向量的线性运算
例:
二.空间向量的线性运算
练一练:
2.
名称 概念 记法
零向量
单位向量
相反向量
共线向量或 平行向量
相等向量
与向量a长度相等而方向相反的向量,叫做a的相反向量
长度为0的向量
模为1的向量
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量
方向相同且模相等的向量
∥
小结:
小结:
1.1.1 空间向量及其运算
高中数学
选择性必修
空间向量
空间向量的基本概念(重点)
空间向量的线性运算(重点)
1
2
共线、共面定理
3
空间向量的基本概念
01
一.空间向量的概念
章前图展示的是一个做滑翔伞运动的场景.
在滑翔过程中,飞行员会受到来自不同方向、大小各异的力,例如绳索的拉力、风力、重力等,显然,这些力不在同一个平面内.
平面向量
空间向量
类比的方法
平面向量
一.空间向量的概念
空间中具有大小和方向的量叫做空间向量,
空间向量的大小叫做空间向量的长度或模.
表示:用字母a,b,c,…表示,或用有向线段表示,
有向线段的长度表示向量的模,a的起点是A,终点是B,
则a也可记作AB,其模记为|a|或|AB|.
A
B
a
O
C
A
B
一.空间向量的概念
O
C
A
B
零向量:规定长度为0的向量叫零向量,
记为0.
单位向量:模为1的向量叫单位向量.
相反向量:与向量a长度相等而方向相
反的向量,称为a的相反向
量,记为-a.
特殊向量
一.空间向量的概念
共线向量:如果表示若干空间向量的有向线段所在的直线互相平
行或重合,那么这些向量叫做共线向量或平行向量。
规定:零向量与任意向量平行,即对于任意向量a,都有0//a
a
b
c
一.空间向量的概念
相等向量:方向相同且模相等的向量称为相等向量,
同向且等长的有向线段表示同一向量或相等向量.
空间向量是自由的,所以对于空间中的任意两个非零向量,我们都可以通过平移使它们的起点重合.因为两条相交直线确定一个平面,所以起点重合的两个不共线向量可以确定一个平面,也就是说,任意两个空问向量都可以平移到同一个平面内,成为同一平面内的两个向量。
如图,已知空间向量a,b,以任意点O为起点,作向量OA=a,OB=b,我们就可以把它们平移到同一个平面a内.
a
b
a
b
O
A
B
b
结论:空间任意两个向量都可以平移到同一个平面内,所以它们 可用同一平面内的两条有向线段表示.
因此凡是涉及空间任意两个向量的问题,平面向量
中有关结论仍适用于它们.
思考:空间中任意两个向量是否一定能够平移到同一个平面内?
一.空间向量的概念
空间向量的线性运算
02
加减运算
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(1)空间向量加法运算:
平行四边形法则:
三角形法则:
注:首尾顺次相接,起点指向终点
二.空间向量的线性运算
三角形法则推广
首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
在空间中,任意两个向量都可以平移到同一个平面内,所以空间向量的加法和减法运算与平面向量相同.
(2)空间向量的减法运算:
注:起点相同,差向量为减向量终点指向被减向量的终点
二.空间向量的线性运算
二.空间向量的线性运算
数乘运算
向量的加、减、数乘运算统称向量的线性运算.
二.空间向量的线性运算
二.空间向量的线性运算
例:
二.空间向量的线性运算
练一练:
2.
名称 概念 记法
零向量
单位向量
相反向量
共线向量或 平行向量
相等向量
与向量a长度相等而方向相反的向量,叫做a的相反向量
长度为0的向量
模为1的向量
如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量
方向相同且模相等的向量
∥
小结:
小结:
