期中复习课件五年级下册数学沪教版(共26张PPT)
文档属性
| 名称 | 期中复习课件五年级下册数学沪教版(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
期中复习
五年级第二学期
体积的复习
1、用一根18分米长的铁丝围成一个最大的正方体框架,这个正方体的体积是( )立方分米。
2、把一个棱长是10分米的正方体钢块熔铸 成一块长20分米,宽5分米的长方体钢板,求钢板的厚度是( )分米。。
填空
棱长:18÷12=1.5(分米)
体积:
V=a
=1.5×1.5×1.5
=3.375(立方分米)
3.375
体积:
V=a
=10×10×10
=1000(立方分米)
正方体体积=长方体体积
长方体的高:
h=V÷a÷b
=1000×20×5
=10(分米)
10
解:设钢板的厚度是x分米。
10×10×10=20×5×x
1000=100x
X=10
3、一个长方体,长是12分米,宽是10分米,高是7分米,从中截取一个最大的正方体木块,剩下部分的体积是( )立方分米。
填空
截取一个棱长为7分米的正方体
V长=abh
=12×10×7
=840(立方分米)
V正=a
=7×7×7
=343(立方分米)
V剩余=V长-V正
=840-343
=497(立方分米)
497
4、用棱长为2厘米的小立方体搭成下图形状,它的体
积为( )立方厘米。
一个正方体的体积:2×2×2=8(cm3)
2
2
5
10
共:19
单个体积×个数:8×19=152(cm3)
152
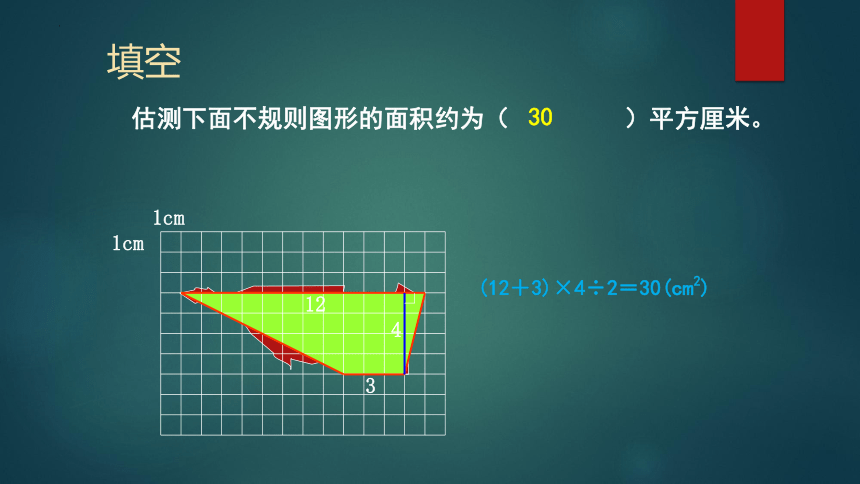
填空
估测下面不规则图形的面积约为( )平方厘米。
1cm
1cm
12
4
3
(12+3)×4÷2=30(cm2)
30
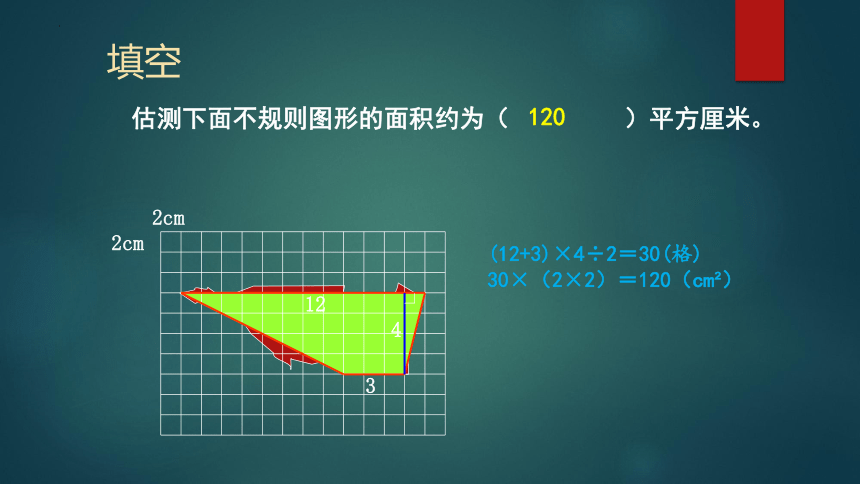
填空
估测下面不规则图形的面积约为( )平方厘米。
2cm
2cm
12
4
3
(12+3)×4÷2=30(格)
30×(2×2)=120(cm )
120
填空
列方程解决问题
(综合复习)
五年级数学第二学期
想一想,列方程解决问题的关键是什么?
等量关系!
哪些方法可以帮助我们找到等量关系?
2、找关键句
3、画图
1、想公式
一个面积为76平方厘米的梯形,上底和下底的和是38厘米,求这个梯形的高是多少厘米?
想:S=(a+b)h÷2
解:设梯形的高是x厘米。
想公式
38x÷2 = 76
这样等量关系明显的问题,直接设未知数就可以列出方程!
五年级某班男生和女生一共36人,女生人数是男生的2倍,
男生和女生各有多少人?
女生人数 = 男生人数×2
男生人数+女生人数 = 36
解:设男生有x人,则女生有2x人。
x+2x=36
和倍问题
和
倍
写设句
写等量关系
解:设男生有x人,则女生有(36- x)人。
36-x = 2x
倍
写等量关系
和
写设句
五年级某班女生人数比男生多6人,女生人数是男生的2倍,
男生和女生各有多少人?
女生人数 = 男生人数×2
女生人数-男生人数 = 6
解:设男生有x人,那么女生有2x人。
2x- x = 6
差倍问题
差
倍
写设句
写等量关系
解:设男生有x人,那么女生有(x+6)人。
x +6 = 2x
倍
写等量关系
差
写设句
果园里梨树比苹果树少12棵,两种树一共有280棵.
问:梨树与苹果树各有多少棵
苹果树的数量 + 梨树的数量 = 280
解:设苹果树有x棵,
则梨树有(x-12 )棵.
x+(x-12)=280
和差问题
差
和
设句有几种写法?
解:设苹果树有x棵,
则梨树有(280-x )棵.
(280-x)= x-12
解:设梨树有x棵,
则苹果树有(x+12 )棵.
x+(x+12)=280
解:设梨树有x棵,
则苹果树有(280-x )棵.
x =(280-x)- 12
写设句
列方程
梨树的数量 = 苹果树的数量 - 12
客船与货船分别从同个港口同时出发,背向而行。客船平均每小时行48千米,经过8小时后,两船相距1280千米,货船平均每小时行多少千米?
客船行的路程+货船行的路程 = 总路程
解:设货船每小时行驶x千米。
48×8+8x = 1280
1280千米
客船
货船
48千米/时
?千米/时
8小时
画图
乙行的路程
甲行的路程
20千米
420千米
甲行的路程 + 乙行的路程 + 20千米 = 420千米
解:设x小时后两车相距420千米。
45×4 + 4x + 20 = 420
画图
甲车和乙车从相距20千米的两地同时出发,背向而行。
甲车平均每小时行45千米,经过4小时后,两车相距420千米,乙车平均每小时行多少千米?
小丁丁、小巧锻炼身体,小巧跑出400米后小丁丁从起点出发,小丁丁平均每分钟跑200米,小巧平均每分钟跑180米,当小丁丁追上小巧时,小巧总共跑了几米?
先求时间
解:设X分钟后小丁丁追上小巧
400+180x=200x
x=20
再求路程
400+180×20=4000(米)
答:当小丁丁追上小巧时,
小巧总共跑了4000米。
小巧先行路程 + 小巧后先行路程 = 小丁丁的路程
400 m
小丁丁
小巧
A
B
200米/分
180米/分
画图
一列慢车从A站出发,每小时行驶60千米,一列快车也从A站出发,每小时行驶80千米,同向而行,快车先行半小时,慢车再出发,当快车到达B站时,慢车离乙地还有166千米,这时慢车行驶了多少小时?
A
慢车
快车
166千米
解:设这时慢车行驶了x小时。
60X + 166 = 80×0.5+80x
慢车行的路程 + 未行的路程 = 快车先行的路程+快车后行的路程
B
60x
80x
画图
画图找到主要关系,清楚表示分步关系。
一个学生从家到学校,如果用每分钟50米的速度走,
他上课就要迟到8分钟。如果用每分钟60米的速度前进,
就能早到5分钟,这个学生家到学校的距离是多少?
50 (x+8) = 60 (x-5)
家到学校的路程 = 家到学校的路程
解:设准时到校需要x分钟。
有一堆黑、白两色的棋子,黑子的数量是白子的2倍,每次取4枚黑子,3枚白子。若干次后,白子刚好取完,黑子还有16枚。一共取了多少次?黑、白子有多少枚?
黑子的数量 = 白子的数量 ×2
解:设一共取了x次,则黑子有(4x+16)枚,白子有3x枚。
4x + 16
= 3x
每次取得子数×取的次数
每次取得子数×取的次数
+16
×2
×2
掌握基本题了吗?
接下来是进阶题!
有两根同样长的木料,如果第一根锯去2米,第二根锯去3.5米,那么第一根剩余木料的长就是第二根剩下长的2.5倍。原来两根木料各长多少米?
现在第一根木料的长度=现在第二根木料的长度×2.5
解:设原来第一根木料长x米,
则原来第二根木料也长x米。
x-2=2.5(x-3.5)
x-2=2.5x-8.75
2.5x-x=8.75-2
1.5x=6.75
x=4.5
答:原来两根木料各长4.5米。
检验:
4.5-2=2.5
4.5-3.5=1
2.5÷1=2.5
x-2
x-3.5
x
小明和小红在400米的环形跑道上练习赛跑,
小红的速度为100米/分,小明的速度为150米/分。
(1)如果他们从同一地点同时相背而行,几分钟后可以第二次相遇?
小明
150米/分
小红
100米/分
小明跑的路程+小红跑的路程=环形跑道的总长
解:设x分钟后可以第二次相遇。
150x+100x=400×2
小明和小红在400米的环形跑道上练习赛跑,
小红的速度为100米/分,小明的速度为150米/分。
(2)如果他们从同一地点同时同向而行,几分钟后可以第二次相遇?
小明
150米/分
小红
100米/分
小红跑的路程+环形跑道的总长=小明跑的路程
解:设x分钟后可以第二次相遇。
100x+400×2=150x
一辆慢车从A站出发,每小时行驶60千米,一辆快车也从A站出发,每小时行驶80千米,背向而行。经过6分钟快车司机突然想起手机落在慢车司机车上,于是立即调头去追。那么快车追上慢车还需要几小时?
A
相当于两车相距的路程
解:设快车追上慢车还需要x小时。
0.1×60+0.1×80 + 60X = 80X
相距的路程 + 慢车后行的路程 = 快车行的路程
两列火车同时从A、B两站出发,相向而行,甲车每小时行驶60千米,乙车每小时行驶80千米,最后在距离中点35千米处相遇,求相遇时两车开了多少小时?
解:相遇时两车开了 X 小时。
60x
甲车行路程 + 乙车行的路程 = 总路程 ?
甲车行路程 + 35=乙车行的路程 - 35
+35
= 80x
-35
A
B
甲车
乙车
中点
一半的路程 = 一半的路程
同学们去划船,如果每只船坐4人,则少3只船;如果每只船坐6人,就空2个位子。共租了几只船?划船的同学有多少人?
“每只船坐4人”的总人数=“每只船坐6人”的总人数
解:设共租了x只船,则划船的同学有4(x+3)人。
4(x+3) =6x-2
4x+12=6x-2
每只船坐4人×船数
x+3
4
每只船坐6人×船数
x
6
4(x+3)
=4×(7+3)
=4×10
=40
答:共租了7只船,划船的同学有40人。
-2
4x + 12-4x = 6x-2-4x
12 = 2x-2
2x = 14
x = 7
期中复习
五年级第二学期
体积的复习
1、用一根18分米长的铁丝围成一个最大的正方体框架,这个正方体的体积是( )立方分米。
2、把一个棱长是10分米的正方体钢块熔铸 成一块长20分米,宽5分米的长方体钢板,求钢板的厚度是( )分米。。
填空
棱长:18÷12=1.5(分米)
体积:
V=a
=1.5×1.5×1.5
=3.375(立方分米)
3.375
体积:
V=a
=10×10×10
=1000(立方分米)
正方体体积=长方体体积
长方体的高:
h=V÷a÷b
=1000×20×5
=10(分米)
10
解:设钢板的厚度是x分米。
10×10×10=20×5×x
1000=100x
X=10
3、一个长方体,长是12分米,宽是10分米,高是7分米,从中截取一个最大的正方体木块,剩下部分的体积是( )立方分米。
填空
截取一个棱长为7分米的正方体
V长=abh
=12×10×7
=840(立方分米)
V正=a
=7×7×7
=343(立方分米)
V剩余=V长-V正
=840-343
=497(立方分米)
497
4、用棱长为2厘米的小立方体搭成下图形状,它的体
积为( )立方厘米。
一个正方体的体积:2×2×2=8(cm3)
2
2
5
10
共:19
单个体积×个数:8×19=152(cm3)
152
填空
估测下面不规则图形的面积约为( )平方厘米。
1cm
1cm
12
4
3
(12+3)×4÷2=30(cm2)
30
填空
估测下面不规则图形的面积约为( )平方厘米。
2cm
2cm
12
4
3
(12+3)×4÷2=30(格)
30×(2×2)=120(cm )
120
填空
列方程解决问题
(综合复习)
五年级数学第二学期
想一想,列方程解决问题的关键是什么?
等量关系!
哪些方法可以帮助我们找到等量关系?
2、找关键句
3、画图
1、想公式
一个面积为76平方厘米的梯形,上底和下底的和是38厘米,求这个梯形的高是多少厘米?
想:S=(a+b)h÷2
解:设梯形的高是x厘米。
想公式
38x÷2 = 76
这样等量关系明显的问题,直接设未知数就可以列出方程!
五年级某班男生和女生一共36人,女生人数是男生的2倍,
男生和女生各有多少人?
女生人数 = 男生人数×2
男生人数+女生人数 = 36
解:设男生有x人,则女生有2x人。
x+2x=36
和倍问题
和
倍
写设句
写等量关系
解:设男生有x人,则女生有(36- x)人。
36-x = 2x
倍
写等量关系
和
写设句
五年级某班女生人数比男生多6人,女生人数是男生的2倍,
男生和女生各有多少人?
女生人数 = 男生人数×2
女生人数-男生人数 = 6
解:设男生有x人,那么女生有2x人。
2x- x = 6
差倍问题
差
倍
写设句
写等量关系
解:设男生有x人,那么女生有(x+6)人。
x +6 = 2x
倍
写等量关系
差
写设句
果园里梨树比苹果树少12棵,两种树一共有280棵.
问:梨树与苹果树各有多少棵
苹果树的数量 + 梨树的数量 = 280
解:设苹果树有x棵,
则梨树有(x-12 )棵.
x+(x-12)=280
和差问题
差
和
设句有几种写法?
解:设苹果树有x棵,
则梨树有(280-x )棵.
(280-x)= x-12
解:设梨树有x棵,
则苹果树有(x+12 )棵.
x+(x+12)=280
解:设梨树有x棵,
则苹果树有(280-x )棵.
x =(280-x)- 12
写设句
列方程
梨树的数量 = 苹果树的数量 - 12
客船与货船分别从同个港口同时出发,背向而行。客船平均每小时行48千米,经过8小时后,两船相距1280千米,货船平均每小时行多少千米?
客船行的路程+货船行的路程 = 总路程
解:设货船每小时行驶x千米。
48×8+8x = 1280
1280千米
客船
货船
48千米/时
?千米/时
8小时
画图
乙行的路程
甲行的路程
20千米
420千米
甲行的路程 + 乙行的路程 + 20千米 = 420千米
解:设x小时后两车相距420千米。
45×4 + 4x + 20 = 420
画图
甲车和乙车从相距20千米的两地同时出发,背向而行。
甲车平均每小时行45千米,经过4小时后,两车相距420千米,乙车平均每小时行多少千米?
小丁丁、小巧锻炼身体,小巧跑出400米后小丁丁从起点出发,小丁丁平均每分钟跑200米,小巧平均每分钟跑180米,当小丁丁追上小巧时,小巧总共跑了几米?
先求时间
解:设X分钟后小丁丁追上小巧
400+180x=200x
x=20
再求路程
400+180×20=4000(米)
答:当小丁丁追上小巧时,
小巧总共跑了4000米。
小巧先行路程 + 小巧后先行路程 = 小丁丁的路程
400 m
小丁丁
小巧
A
B
200米/分
180米/分
画图
一列慢车从A站出发,每小时行驶60千米,一列快车也从A站出发,每小时行驶80千米,同向而行,快车先行半小时,慢车再出发,当快车到达B站时,慢车离乙地还有166千米,这时慢车行驶了多少小时?
A
慢车
快车
166千米
解:设这时慢车行驶了x小时。
60X + 166 = 80×0.5+80x
慢车行的路程 + 未行的路程 = 快车先行的路程+快车后行的路程
B
60x
80x
画图
画图找到主要关系,清楚表示分步关系。
一个学生从家到学校,如果用每分钟50米的速度走,
他上课就要迟到8分钟。如果用每分钟60米的速度前进,
就能早到5分钟,这个学生家到学校的距离是多少?
50 (x+8) = 60 (x-5)
家到学校的路程 = 家到学校的路程
解:设准时到校需要x分钟。
有一堆黑、白两色的棋子,黑子的数量是白子的2倍,每次取4枚黑子,3枚白子。若干次后,白子刚好取完,黑子还有16枚。一共取了多少次?黑、白子有多少枚?
黑子的数量 = 白子的数量 ×2
解:设一共取了x次,则黑子有(4x+16)枚,白子有3x枚。
4x + 16
= 3x
每次取得子数×取的次数
每次取得子数×取的次数
+16
×2
×2
掌握基本题了吗?
接下来是进阶题!
有两根同样长的木料,如果第一根锯去2米,第二根锯去3.5米,那么第一根剩余木料的长就是第二根剩下长的2.5倍。原来两根木料各长多少米?
现在第一根木料的长度=现在第二根木料的长度×2.5
解:设原来第一根木料长x米,
则原来第二根木料也长x米。
x-2=2.5(x-3.5)
x-2=2.5x-8.75
2.5x-x=8.75-2
1.5x=6.75
x=4.5
答:原来两根木料各长4.5米。
检验:
4.5-2=2.5
4.5-3.5=1
2.5÷1=2.5
x-2
x-3.5
x
小明和小红在400米的环形跑道上练习赛跑,
小红的速度为100米/分,小明的速度为150米/分。
(1)如果他们从同一地点同时相背而行,几分钟后可以第二次相遇?
小明
150米/分
小红
100米/分
小明跑的路程+小红跑的路程=环形跑道的总长
解:设x分钟后可以第二次相遇。
150x+100x=400×2
小明和小红在400米的环形跑道上练习赛跑,
小红的速度为100米/分,小明的速度为150米/分。
(2)如果他们从同一地点同时同向而行,几分钟后可以第二次相遇?
小明
150米/分
小红
100米/分
小红跑的路程+环形跑道的总长=小明跑的路程
解:设x分钟后可以第二次相遇。
100x+400×2=150x
一辆慢车从A站出发,每小时行驶60千米,一辆快车也从A站出发,每小时行驶80千米,背向而行。经过6分钟快车司机突然想起手机落在慢车司机车上,于是立即调头去追。那么快车追上慢车还需要几小时?
A
相当于两车相距的路程
解:设快车追上慢车还需要x小时。
0.1×60+0.1×80 + 60X = 80X
相距的路程 + 慢车后行的路程 = 快车行的路程
两列火车同时从A、B两站出发,相向而行,甲车每小时行驶60千米,乙车每小时行驶80千米,最后在距离中点35千米处相遇,求相遇时两车开了多少小时?
解:相遇时两车开了 X 小时。
60x
甲车行路程 + 乙车行的路程 = 总路程 ?
甲车行路程 + 35=乙车行的路程 - 35
+35
= 80x
-35
A
B
甲车
乙车
中点
一半的路程 = 一半的路程
同学们去划船,如果每只船坐4人,则少3只船;如果每只船坐6人,就空2个位子。共租了几只船?划船的同学有多少人?
“每只船坐4人”的总人数=“每只船坐6人”的总人数
解:设共租了x只船,则划船的同学有4(x+3)人。
4(x+3) =6x-2
4x+12=6x-2
每只船坐4人×船数
x+3
4
每只船坐6人×船数
x
6
4(x+3)
=4×(7+3)
=4×10
=40
答:共租了7只船,划船的同学有40人。
-2
4x + 12-4x = 6x-2-4x
12 = 2x-2
2x = 14
x = 7
同课章节目录
