人教版(新)六上 第三单元 8.工程问题【优质课件】
文档属性
| 名称 | 人教版(新)六上 第三单元 8.工程问题【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 11:14:15 | ||
图片预览







文档简介
(共23张PPT)
工程问题
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
修一段600米长的公路,甲工程队单独做20天完成,由乙工程队单独做30天完成,两队合作多少天完成?
600 ÷20=30(米)
600 ÷30=20(米)
600 ÷(30+20)
=600 ÷50
=12(天)
答:两队合作12天完成。
02
新课精讲
探索新知
探究点
掌握用假设、验证等方法解决问题的基本策略,体会模型思想
如果两队合修,多少天能修完?
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。
探索新知
问题:
①从题目中你知道了什么?
②要解决“两队合修,多少天修完?”这个问
题,需要知道哪些信息?
(这条路的长度“工作总量”;两队1天各
修的长度 “工作效率”)
③如果知道了这两个信息,这个问题可以怎样解决?
(这条路的长度÷(一队1天修的长度 + 二队1天
修的长度))
探索新知
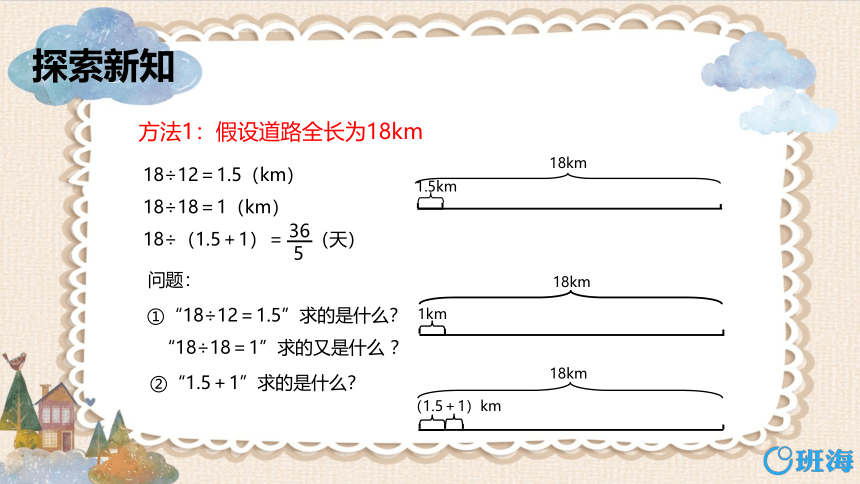
问题:
①“18÷12=1.5”求的是什么?
“18÷18=1”求的又是什么 ?
方法1:假设道路全长为18km
②“1.5+1”求的是什么?
18km
18km
18km
1.5km
1km
(1.5+1)km
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
探索新知
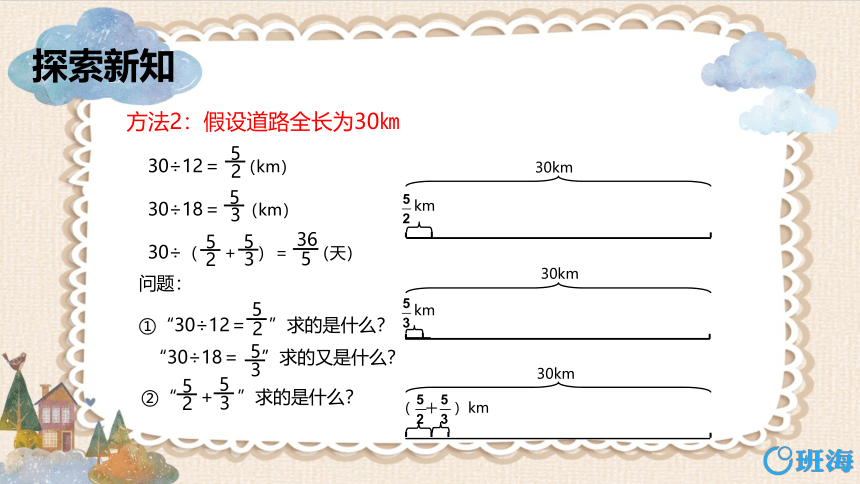
①“30÷12= ”求的是什么?
“30÷18= ”求的又是什么?
2
5
3
5
问题:
方法2:假设道路全长为30㎞
30km
30km
30km
km
km
( )km
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
②“ + ”求的是什么?
2
5
3
5
探索新知
问题:
① 我们假设这条路的长度都不同,但最终的结果是相同的,
那么这条路的长度还可以看做是多少千米?
② 这条路的长度可以看做是“1”吗?
③ 如果把这条路的长度看做是“1”,应该怎样解答?
方法1:
方法2:
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
探索新知
问题:
① 这样列式的依据是什么?
“1”
(工作总量÷工作效率=工作时间)
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
方法3:假设道路全长为“1”
探索新知
“1”
“1”
求的是什么? 呢?
(一队1天修完这条路的几分之几;二队1天修完这条路的几分之几。)
12
1
18
1
③“ + ”求的是什么?
12
1
18
1
探索新知
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
假设全长为18㎞
假设全长为30㎞
假设全长为“1”
要点提示
不管假设这条路有多长,答案都是相同的。把道路长假设成1,解答要简便。
典题精讲
如果两辆车一起运,多少次能运完这批货物?
1÷( + )
6
1
3
1
2
1
=1÷
=2(次)
答:2次能运完这批货物。
易错提醒
一项工程,甲队单独做需要 小时,乙队需要 小时,两队合做,多少小时可以完成?
(小时)
辨析:两个分数后边都有单位“小时”,因此这两个分数是工作时间而不是工作效率。
03
学以致用
小试牛刀
1.一条水渠,甲工程队单独修10天完成,乙工程队单独修15天完成,两队合修,多少天完成?
假设这条水渠长( )米。
2.一批布,单独做上衣可以做40件,单独做裤子可以做60件。如果成套做,一共可以做多少套?
假设这批布有( )米。
答:6天完成。
答:一共可以做24套。
150
120
小试牛刀
3.填一填。
(1)一件工作,甲单独做需要4小时完成,乙单独做需要6小时完成,甲每小时完成这件工作的 ,乙每小时完成这件工作的 ,两人合做,每小时完成这件工作的 。
(2)一批零件,师徒两人合做8天可以完成,徒弟单独做要40天完成,师傅单独做每天完成这批零件的 。
小试牛刀
4.选择。(把正确答案的序号填在括号里)
(1)加工一批服装,甲组单独做每天完成 ,乙组单独做每天完成 ,两组同时加工多少天完成?正确列式是( )
(2)一个游泳池可装水360吨,单开进水管20小时注满水池,单开出水管30小时可把满池水放完,现在同时打开两管,几小时可把水池注满?正确列式是( )。
B
C
小试牛刀
5.解决问题。
(1)一批货物,用小货车运需要12次运完,用大卡车运,只要4次运完。如果两车一起运,多少次运完这批货物?
(2)一辆小汽车从武汉到杭州需要8小时,一辆大客车从杭州到武汉需要10小时。两车同时从两地出发相向而行,几小时相遇?
(次)
(小时)
答:3次运完这批货物。
答: 小时相遇。
04
课堂小结
归纳总结:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
利用抽象的“1”解决实际问题:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(↓↓观看介绍视频↓↓)
工程问题
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
01
课前导入
02
新课精讲
03
学以致用
04
课堂小结
01
课前导入
情景导入
修一段600米长的公路,甲工程队单独做20天完成,由乙工程队单独做30天完成,两队合作多少天完成?
600 ÷20=30(米)
600 ÷30=20(米)
600 ÷(30+20)
=600 ÷50
=12(天)
答:两队合作12天完成。
02
新课精讲
探索新知
探究点
掌握用假设、验证等方法解决问题的基本策略,体会模型思想
如果两队合修,多少天能修完?
一条道路,如果甲队单独修,12天能修完;如果乙队单独修,18天能修完。
探索新知
问题:
①从题目中你知道了什么?
②要解决“两队合修,多少天修完?”这个问
题,需要知道哪些信息?
(这条路的长度“工作总量”;两队1天各
修的长度 “工作效率”)
③如果知道了这两个信息,这个问题可以怎样解决?
(这条路的长度÷(一队1天修的长度 + 二队1天
修的长度))
探索新知
问题:
①“18÷12=1.5”求的是什么?
“18÷18=1”求的又是什么 ?
方法1:假设道路全长为18km
②“1.5+1”求的是什么?
18km
18km
18km
1.5km
1km
(1.5+1)km
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
探索新知
①“30÷12= ”求的是什么?
“30÷18= ”求的又是什么?
2
5
3
5
问题:
方法2:假设道路全长为30㎞
30km
30km
30km
km
km
( )km
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
②“ + ”求的是什么?
2
5
3
5
探索新知
问题:
① 我们假设这条路的长度都不同,但最终的结果是相同的,
那么这条路的长度还可以看做是多少千米?
② 这条路的长度可以看做是“1”吗?
③ 如果把这条路的长度看做是“1”,应该怎样解答?
方法1:
方法2:
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
探索新知
问题:
① 这样列式的依据是什么?
“1”
(工作总量÷工作效率=工作时间)
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
方法3:假设道路全长为“1”
探索新知
“1”
“1”
求的是什么? 呢?
(一队1天修完这条路的几分之几;二队1天修完这条路的几分之几。)
12
1
18
1
③“ + ”求的是什么?
12
1
18
1
探索新知
1÷( + )
= 1÷
= (天)
18
1
12
1
36
5
5
36
30÷12= (km)
30÷18= (km)
30÷( + )= (天)
2
5
3
5
2
5
3
5
5
36
18÷12=1.5(km)
18÷18=1(km)
18÷(1.5+1)= (天)
5
36
假设全长为18㎞
假设全长为30㎞
假设全长为“1”
要点提示
不管假设这条路有多长,答案都是相同的。把道路长假设成1,解答要简便。
典题精讲
如果两辆车一起运,多少次能运完这批货物?
1÷( + )
6
1
3
1
2
1
=1÷
=2(次)
答:2次能运完这批货物。
易错提醒
一项工程,甲队单独做需要 小时,乙队需要 小时,两队合做,多少小时可以完成?
(小时)
辨析:两个分数后边都有单位“小时”,因此这两个分数是工作时间而不是工作效率。
03
学以致用
小试牛刀
1.一条水渠,甲工程队单独修10天完成,乙工程队单独修15天完成,两队合修,多少天完成?
假设这条水渠长( )米。
2.一批布,单独做上衣可以做40件,单独做裤子可以做60件。如果成套做,一共可以做多少套?
假设这批布有( )米。
答:6天完成。
答:一共可以做24套。
150
120
小试牛刀
3.填一填。
(1)一件工作,甲单独做需要4小时完成,乙单独做需要6小时完成,甲每小时完成这件工作的 ,乙每小时完成这件工作的 ,两人合做,每小时完成这件工作的 。
(2)一批零件,师徒两人合做8天可以完成,徒弟单独做要40天完成,师傅单独做每天完成这批零件的 。
小试牛刀
4.选择。(把正确答案的序号填在括号里)
(1)加工一批服装,甲组单独做每天完成 ,乙组单独做每天完成 ,两组同时加工多少天完成?正确列式是( )
(2)一个游泳池可装水360吨,单开进水管20小时注满水池,单开出水管30小时可把满池水放完,现在同时打开两管,几小时可把水池注满?正确列式是( )。
B
C
小试牛刀
5.解决问题。
(1)一批货物,用小货车运需要12次运完,用大卡车运,只要4次运完。如果两车一起运,多少次运完这批货物?
(2)一辆小汽车从武汉到杭州需要8小时,一辆大客车从杭州到武汉需要10小时。两车同时从两地出发相向而行,几小时相遇?
(次)
(小时)
答:3次运完这批货物。
答: 小时相遇。
04
课堂小结
归纳总结:
工程问题是分数问题的特例,工作总量与工作效率都不是具体的数,而是用抽象的分数来表示。
一般地,工作总量用单位“1”来表示,工作效率则用完成总量所需时间的倒数来表示。
利用抽象的“1”解决实际问题:
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(↓↓观看介绍视频↓↓)
