人教版七年级上册1.5.2 科学记数法 课件(共19张PPT)
文档属性
| 名称 | 人教版七年级上册1.5.2 科学记数法 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-10 21:44:17 | ||
图片预览






文档简介
(共19张PPT)
1.5.2科学计数法
第一章 有理数
教学目标
会用科学计数法表示大数。 (重点)
掌握科学计数法的写法。 (重点)
会用科学计数法表示绝对值较大的数。(难点)
嫦娥奔月
大家知道嫦娥奔月的故事吗?月球距离 地球有多远,怎么表示呢?
思维激发
月球到地球的平均距离是384,403.9千米
月球离地球近地点距离为363,300千米
月球距离地球最远的远地点距离为405,493千米
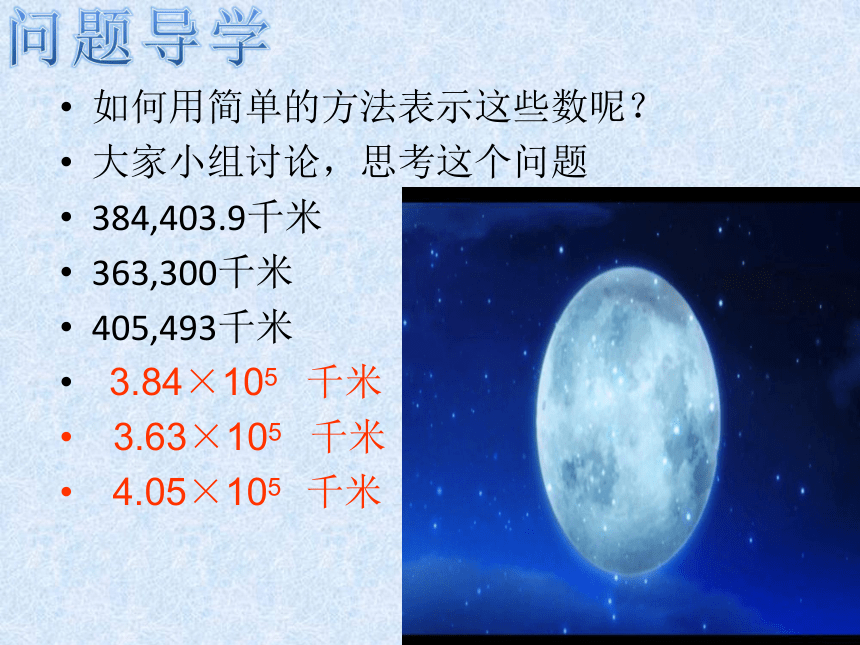
如何用简单的方法表示这些数呢?
大家小组讨论,思考这个问题
384,403.9千米
363,300千米
405,493千米
3.84×105 千米
3.63×105 千米
4.05×105 千米
问题导学
合作交流
1、大家知道为什么可以这样表示吗?
2、大家知道105是什么意思吗?
3、大家还知道哪些大数可以用这种方法表示
?
探析建构
用简单方法表示大数
696 000 km
300 000 00m/s
6.96×105 千米
3×107 米
探析建构
展示
集体探究
10的乘方有如下的特点:
…
一般地,10的n次幂等于10···0(在1的后面有n个0),所以就可以用10的乘方表示一些大数.
你知道
分别等于多少吗?
的意义和规律是什么?
书写简短,便于读数.
读作:9乘10的4次方(幂)
例如:90 000 = 9×10 000 = 9×104
696 000 = 6.96×100 000
= 6.96×105
7 000 000 000= 7×1 000 000 000
=7×109
300 000 000 = 3×100 000 000
= 3×108
你能看出这样表示的奥妙吗?
归纳与概括
像这样,把一个大于10的数表示成 ×
10n的形式(其中 是整数数位只有一位的数, n为正整数),这种记数方法叫做科学记数法.
1. 用科学记数法表示下列各数:
探析建构
①32 000 ②384 000 000
③-810 000 ④9 410 000
=3.2×104
= - 8.1×105
=3.84×108
=9.41×106
思考:等号左边整数的位数与右边10的指数有
什么关系?用科学记数法表示一个n 位整数,其中10的指数是 .
n-1
2.下列各数是否是用科学记数法表示的?
×
×
2 400 000
2 400 000
3 100 000
3 100 000
整数数位只有一位
探析建构
3.下列用科学记数法表示的数,原数是什么?
=32 000
=6 000
=32 500 000
练一练,你一定行
1.用科学记数法写出下列各数:
10 000, 800 000, 56 000 000, -7 400 000.
2.下列用科学记数法写出的数,原来分别是什么数?
1×107 4×103
8.5×106 7.04×105
=104
=8×105
=5.6×107
=-7.4×106
=10 000 000
=4 000
=8 500 000
=704 000
-3.96×104
=-39 600
二,试一试你的身手,想好了再填
1.用科学计数法表示的原数4×103 =
2.用科学计数法表示的原数2.05x105=
3.用科学计数法表示的原数-2.17x106=
4.已知某种型号的纸100张的厚度约为1cm,那么这种型号的纸13亿张的厚度约为
5.2006年我国公民义务植树运动开展25周年,25年来我市累计植树154000000株,这个数字可以用科学记数法表示为 株.
4000
205000
-2170000
1.3x102 km
1.54x108
训练迁移
大家谈谈
一个正常人的平均心跳速率约为每分70次,一年(取365天)大约跳多少次?用科学记数法表示这一结果,一个正常人一生心跳次数能达到1亿次吗?请说明理由.
扩展延伸
解:因为1年=365天=365×24×60(分),
所以一年心跳次数约为:
365×24×60×70=
=3.679 2×107(次);
108÷( 3.6792×107 )
≈2.7(年),
因为心跳达到1亿次需要的时间是:
所以一个正常人一生心跳次数能达到1亿次.
36 792 000
总 结
1.本节课你学习了什么
2.本节课你有哪些收获?
3.通过学习,你想探究的问题是什么?
1.教科书第47页习题1.5第4、5题.
2.补充作业:
课后作业
(1)用科学记数法表示下列各数:
①900 200 ②300
③10 000 000 ④-510 000
(2)已知下列用科学记数法表示的数,写出原来的数.
①2.01×104 ②6.070×105
③6×105 ④104
(3)用科学记数法表示下列各小题中的量:
①银河系中的恒星约有160 000 000 000颗;
②地球离太阳大约有一亿五千万千米.
1.5.2科学计数法
第一章 有理数
教学目标
会用科学计数法表示大数。 (重点)
掌握科学计数法的写法。 (重点)
会用科学计数法表示绝对值较大的数。(难点)
嫦娥奔月
大家知道嫦娥奔月的故事吗?月球距离 地球有多远,怎么表示呢?
思维激发
月球到地球的平均距离是384,403.9千米
月球离地球近地点距离为363,300千米
月球距离地球最远的远地点距离为405,493千米
如何用简单的方法表示这些数呢?
大家小组讨论,思考这个问题
384,403.9千米
363,300千米
405,493千米
3.84×105 千米
3.63×105 千米
4.05×105 千米
问题导学
合作交流
1、大家知道为什么可以这样表示吗?
2、大家知道105是什么意思吗?
3、大家还知道哪些大数可以用这种方法表示
?
探析建构
用简单方法表示大数
696 000 km
300 000 00m/s
6.96×105 千米
3×107 米
探析建构
展示
集体探究
10的乘方有如下的特点:
…
一般地,10的n次幂等于10···0(在1的后面有n个0),所以就可以用10的乘方表示一些大数.
你知道
分别等于多少吗?
的意义和规律是什么?
书写简短,便于读数.
读作:9乘10的4次方(幂)
例如:90 000 = 9×10 000 = 9×104
696 000 = 6.96×100 000
= 6.96×105
7 000 000 000= 7×1 000 000 000
=7×109
300 000 000 = 3×100 000 000
= 3×108
你能看出这样表示的奥妙吗?
归纳与概括
像这样,把一个大于10的数表示成 ×
10n的形式(其中 是整数数位只有一位的数, n为正整数),这种记数方法叫做科学记数法.
1. 用科学记数法表示下列各数:
探析建构
①32 000 ②384 000 000
③-810 000 ④9 410 000
=3.2×104
= - 8.1×105
=3.84×108
=9.41×106
思考:等号左边整数的位数与右边10的指数有
什么关系?用科学记数法表示一个n 位整数,其中10的指数是 .
n-1
2.下列各数是否是用科学记数法表示的?
×
×
2 400 000
2 400 000
3 100 000
3 100 000
整数数位只有一位
探析建构
3.下列用科学记数法表示的数,原数是什么?
=32 000
=6 000
=32 500 000
练一练,你一定行
1.用科学记数法写出下列各数:
10 000, 800 000, 56 000 000, -7 400 000.
2.下列用科学记数法写出的数,原来分别是什么数?
1×107 4×103
8.5×106 7.04×105
=104
=8×105
=5.6×107
=-7.4×106
=10 000 000
=4 000
=8 500 000
=704 000
-3.96×104
=-39 600
二,试一试你的身手,想好了再填
1.用科学计数法表示的原数4×103 =
2.用科学计数法表示的原数2.05x105=
3.用科学计数法表示的原数-2.17x106=
4.已知某种型号的纸100张的厚度约为1cm,那么这种型号的纸13亿张的厚度约为
5.2006年我国公民义务植树运动开展25周年,25年来我市累计植树154000000株,这个数字可以用科学记数法表示为 株.
4000
205000
-2170000
1.3x102 km
1.54x108
训练迁移
大家谈谈
一个正常人的平均心跳速率约为每分70次,一年(取365天)大约跳多少次?用科学记数法表示这一结果,一个正常人一生心跳次数能达到1亿次吗?请说明理由.
扩展延伸
解:因为1年=365天=365×24×60(分),
所以一年心跳次数约为:
365×24×60×70=
=3.679 2×107(次);
108÷( 3.6792×107 )
≈2.7(年),
因为心跳达到1亿次需要的时间是:
所以一个正常人一生心跳次数能达到1亿次.
36 792 000
总 结
1.本节课你学习了什么
2.本节课你有哪些收获?
3.通过学习,你想探究的问题是什么?
1.教科书第47页习题1.5第4、5题.
2.补充作业:
课后作业
(1)用科学记数法表示下列各数:
①900 200 ②300
③10 000 000 ④-510 000
(2)已知下列用科学记数法表示的数,写出原来的数.
①2.01×104 ②6.070×105
③6×105 ④104
(3)用科学记数法表示下列各小题中的量:
①银河系中的恒星约有160 000 000 000颗;
②地球离太阳大约有一亿五千万千米.
