第一章《反比例函数》单元测试卷《标准难度》(含答案)
文档属性
| 名称 | 第一章《反比例函数》单元测试卷《标准难度》(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 216.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 19:14:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
湘教版初中数学九年级上册第一章《反比例函数》单元测试卷
考试范围:第一章;考试时间:120分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
下列函数中,是的反比例函数的是( )
A. B. C. D.
如图,长方体的体积是,底面一边长为记底面另一边长为,底面的周长为,长方体的高为当在一定范围内变化时,和都随的变化而变化,则与,与满足的函数关系分别是( )
A. 一次函数关系,二次函数关系
B. 反比例函数关系,二次函数关系
C. 反比例函数关系,一次函数关系
D. 一次函数关系,反比例函数关系
给出的六个关系式:,其中是的反比例函数是( )
A. B. C. D.
若函数是反比例函数,则必须满足( )
A. B.
C. 或 D. 且
已知点、、在反比例函数的图象上,当时,、、的大小关系( )
A. B. C. D.
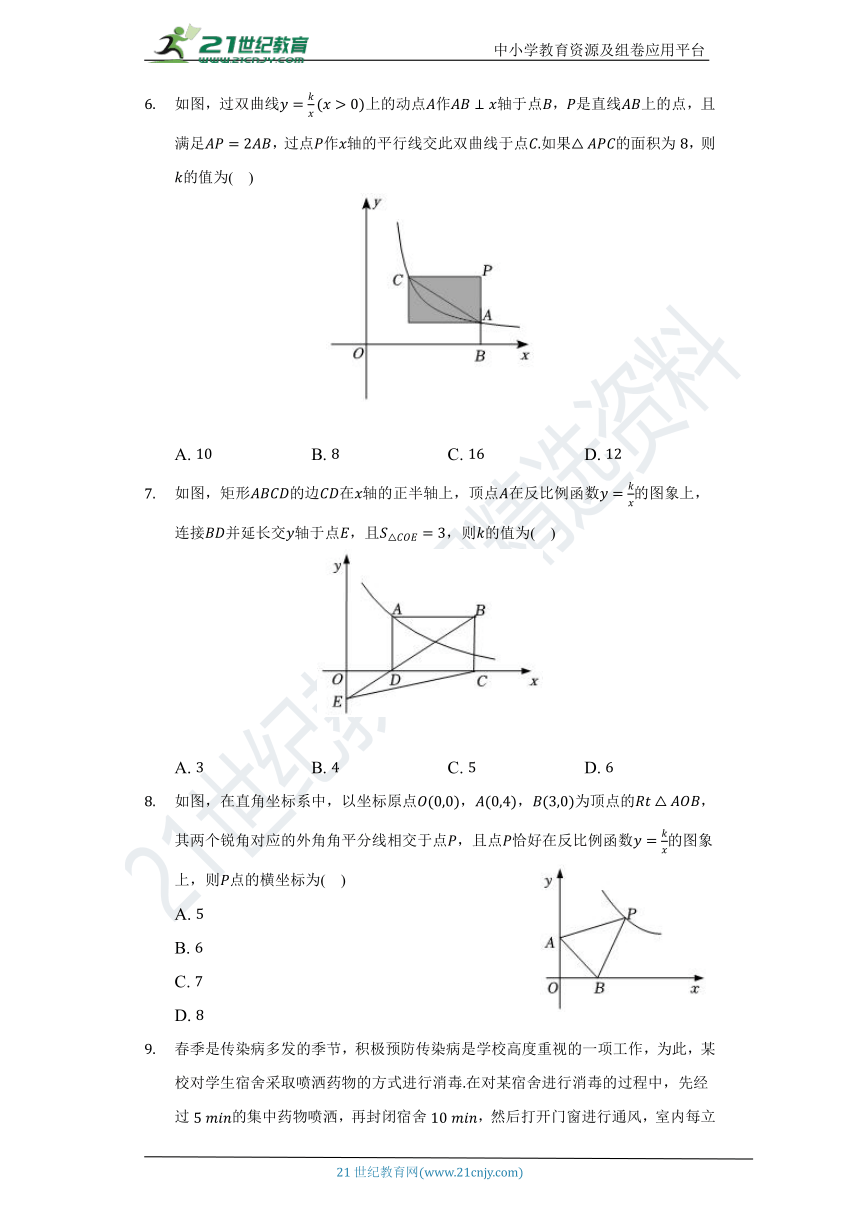
如图,过双曲线上的动点作轴于点,是直线上的点,且满足,过点作轴的平行线交此双曲线于点如果的面积为,则的值为( )
A. B. C. D.
如图,矩形的边在轴的正半轴上,顶点在反比例函数的图象上,连接并延长交轴于点,且,则的值为( )
A. B. C. D.
如图,在直角坐标系中,以坐标原点,,为顶点的,其两个锐角对应的外角角平分线相交于点,且点恰好在反比例函数的图象上,则点的横坐标为( )
A.
B.
C.
D.
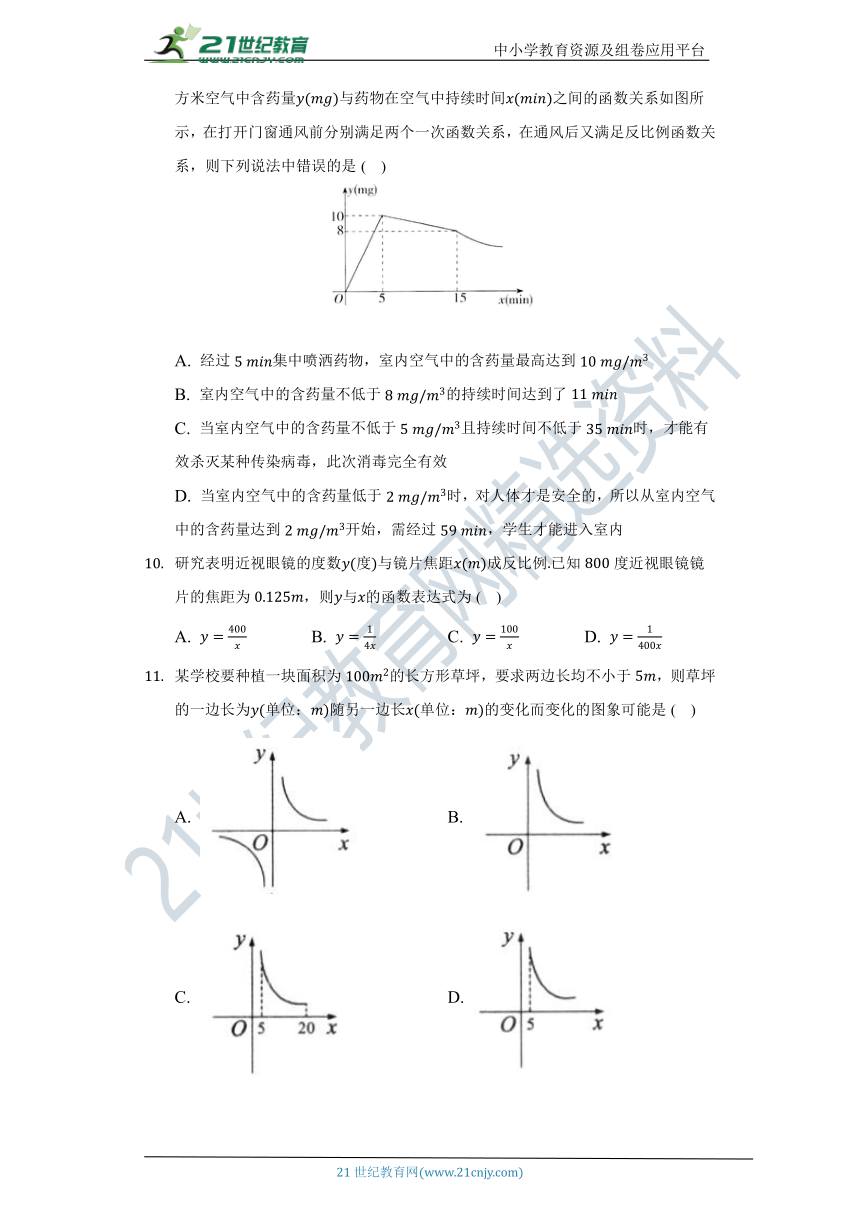
春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物的方式进行消毒在对某宿舍进行消毒的过程中,先经过的集中药物喷洒,再封闭宿舍,然后打开门窗进行通风,室内每立方米空气中含药量与药物在空气中持续时间之间的函数关系如图所示,在打开门窗通风前分别满足两个一次函数关系,在通风后又满足反比例函数关系,则下列说法中错误的是( )
A. 经过集中喷洒药物,室内空气中的含药量最高达到
B. 室内空气中的含药量不低于的持续时间达到了
C. 当室内空气中的含药量不低于且持续时间不低于时,才能有效杀灭某种传染病毒,此次消毒完全有效
D. 当室内空气中的含药量低于时,对人体才是安全的,所以从室内空气中的含药量达到开始,需经过,学生才能进入室内
研究表明近视眼镜的度数度与镜片焦距成反比例已知度近视眼镜镜片的焦距为,则与的函数表达式为( )
A. B. C. D.
某学校要种植一块面积为的长方形草坪,要求两边长均不小于,则草坪的一边长为单位:随另一边长单位:的变化而变化的图象可能是( )
B.
C. D.
某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片烂泥湿地,他们发现,当人和木板对湿地的压力一定时,人和木板对地面的压强随着木板面积的变化而变化,如果人和木板对湿地地面的压力合计,那么下列说法正确的是( )
A. 与的函数表达式为
B. 当越来越大时,也越来越大
C. 若压强不超过时,木板面积最多
D. 当木板面积为时,压强是
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
已知与成反比例,比例系数为,与成正比例,比例系数为,和是已知数,且,则关于成______比例.填“正”或“反”
若与成正比例,与成反比例,与成正比例,与成反比例,则与成______比例.
若点,在反比例函数的图象上,则 ______ 填“”或“”或“”
一辆汽车前灯电路上的电压保持不变,选用灯泡的电阻为,通过的电流强度为,由欧姆定律可知,当电阻为时,测得通过的电流强度为为保证电流强度不低于且不超过,则选用灯泡电阻的取值范围是______.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
已知,与成正比例函数关系,与成反比例函数关系,且时,;时,.
求与之间的函数表达式;
当时,求的值.
已知,与成正比例,与成反比例.当时,;当时,.求关于的函数表达式;
求当时的值.
在面积为定值的一组菱形中,当菱形的一条对角线长为时,它的另一条对角线长为.
设菱形的两条对角线的长分别为,,求关于的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.
若其中一个菱形的一条对角线长为,求这个菱形的边长.
如图,一次函数的图象与反比例函数在第一象限的图象交于和两点,与轴交于点.
求反比例函数的解析式;
若点在轴上,且的面积为,求点的坐标.
如图,在平面直角坐标中,点是坐标原点,一次函数与反比例函数的图象交于、两点.
求直线的解析式及面积;
根据图象写出当时,的取值范围;
若点在轴上,求的最小值.
在平面直角坐标系中,直线:与轴交于点,与轴交于点双曲线与直线交于,两点,其中点的纵坐标大于点的纵坐标.
求点的坐标;
当点的横坐标为时,求的值;
连接,记的面积为若,结合函数图象,直接写出的取值范围.
已知蓄电池的电压为定值,使用蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
请写出这个反比例函数解析式;
蓄电池的电压是多少?
下表中的、、的值分别是多少?
如果以此蓄电池为电源的用电器的限制电流不能超过,那么用电器可变电阻应控制在什么范围?
某气球内充满一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.
写出这个函数的表达式;
当气体体积为时,气压是多少?
当气球内的气压大于时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
受疫情影响,小林为了生计摆地摊,到批发市场进一批单价元的小商品,在夜市营销中统计该批商品的销售单价元与日销售量个之间有如下关系:
猜测并确定与之间的函数关系式;
设经营此小商品的销售利润为元,求出与之间的函数关系式.若物价局规定此小商品的售价最高不能超过元个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
销售单价元
日销售量个
答案和解析
1.【答案】
【解析】解:如果两个变量、之间的关系可以表示成为常数,的形式,那么称是的反比例函数.
故选:.
根据反比例函数的定义即可求出答案.
本题考查反比例函数的定义,解题的关键是熟练运用反比例函数的定义,本题属于基础题型.
2.【答案】
【解析】解:由底面的周长公式:底面周长长宽,
可得:,
即:.
与的关系为:一次函数关系.
根据长方体的体积公式:长方体体积长宽高,
可得:,
,
与的关系为:反比例函数关系.
故选:.
根据底面的周长公式“底面周长长宽“可表示出与的关系式,根据长方体的体积公式“长方体体积长宽高”可表示出与,根据各自的表达式形式判断函数类型即可.
此题考查了函数关系式的综合应用,涉及到一次函数,二次函数,反比例函数等知识,熟知函数的相关类型并能够根据实际问题列出函数关系式是解决本题的关键.
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】解:反比例函数的图象在二四象限,在每个象限内随的增大而增大,
又
点和在第二象限、而在第四象限,
于是有:,而,
因此,
故选:.
在反比例函数的图象在二四象限,根据,可以确定点、、所在象限,根据反比例函数的图象和性质,可以确定、、的大小关系.
考查反比例函数的图象和性质,即函数的增减性.
6.【答案】
【解析】解:设点的坐标为,
,轴,
点的坐标为,
,
的面积为,
,
解得,.
故选:.
设点的坐标为,由确定点的坐标,根据的面积为,列等式可解答.
本题考查的是反比例函数图象上点的坐标特征,根据坐标表示出线段的长度是解题的关键.
7.【答案】
【解析】解:双曲线经过点,
设,
则,,
矩形,
,
,
,.
∽.
,
.
.
.
.
.
故选:.
先用含的代数式表示的面积,再求.
本题考查求反比例的,通过相似三角形边的关系将三角形的面积用含的代数式表示是求解本题的关键.
8.【答案】
【解析】解:如图,过点分别作轴,轴,的垂线,垂足分别为、、,
、分别是两锐角相应的外角平分线,
,
四边形是正方形,
由角平分线的对称性可知,,,
在中,,
设,则,,
由于得,
,
解得,
即,
,
故选:.
根据角平分线的性质可得,进而得出四边形是正方形,由角平分线的对称性得出,,由勾股定理求出,设,列方程求出的值,进而确定点的横坐标.
本题考查反比例函数图象上点的坐标特征,角平分线的性质以及直角三角形的性质,掌握反比例函数图象上点的坐标特征以及勾股定理是解决问题的前提.
9.【答案】
【解析】解:由已知得,
当时,函数解析式为
当时,函数解析式为
当时,函数解析式为.
由题图知,选项不符合题意
当时,或,
室内空气中的含药量不低于的持续时间达到了,
故B选项不符合题意
当时,或,,
故C选项符合题意
当时,或,,
从室内空气中的含药量达到开始,
需经过,学生才能进入室内,
故D选项不符合题意.
综上,选C.
故选C.
10.【答案】
【解析】
【分析】
本题考查了根据实际问题列反比例函数关系式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.反比例函数的一般形式为是常数,且,常用待定系数法求解函数解析式设出反比例函数解析式,把代入即可求解.
【解答】
解:设,
度近视眼镜镜片的焦距为,
即,,
,
.
故选C.
11.【答案】
【解析】
【分析】
本题考查反比例函数的图象,反比例函数的应用,根据反比例函数解析式确定的取值范围,即可求得的取值范围,熟练掌握实际问题的反比例函数图象是解题的关键,易知是的反比例函数,再根据边长的取值范围即可解题.
【解答】
解:草坪面积为,
、存在关系,
两边长均不小于,
当时,,
又,
符合条件的是图.
故选C.
12.【答案】
【解析】解:压力一定时,压强和受力面积成反比;
,
,
是的反比例函数,
,
当越来越大时,也越来越小,
故选项A,不符合题意;
当时,
即,
,
若压强不超过时,木板面积最少,
故选项C不符合题意;
当时,,
当木板面积为时,压强是,
故选项D符合题意;
故选:.
压力一定时,压强和受力面积成反比,根据压力为写出解析式,根据解析式即可判定各个选项.
本题考查反比例函数的应用,根据题意写出反比例函数的解析式是解题的关键.
13.【答案】反
【解析】解:与成反比例,比例系数为,
,
与成正比例,比例系数为,
,
,
和是已知数,且,
关于成反比例,
故答案为:反.
根据反比例函数的定义得出,根据正比例函数的定义得出,求出,再根据反比例函数的定义得出答案即可.
本题考查了正比例函数与反比例函数的定义,能熟记正比例函数与反比例函数的定义是解此题的关键.
14.【答案】反
【解析】解:与成正比例,与成反比例,与成正比例,与成反比例,
,,
,
与成反比例,
同理可得:与成反比例,与成正比例,与成正比例,
与成反比例,
比例关系每四个一循环,分别是:正比例,反比例,反比例,正比例关系,
,
与成反比例关系,
故答案为:反.
根据与成正比例,与成反比例,得出,,即可得出,进而得出与成反比例,与成正比例,与成正比例,进而得出与比例关系每四个一循环,进而得出答案.
此题主要考查了正比例函数与反比例函数的关系,利用已知得出与比例关系,每四个一循环是解题关键.
15.【答案】
【解析】解:,
反比例函数的图象在一、三象限,且在每个象限内随的增大而减小,
点,同在第三象限,且,
,
故答案为.
反比例函数的图象在一、三象限,在每个象限内,随的增大而减小,判断出的值的大小关系.
本题考查反比例函数的图象和性质,掌握反比例函数的增减性是解决问题的关键,
16.【答案】
【解析】解:由题意得:
,
当电阻为时,测得通过的电流强度为,
,
,
当时,
,
,
故答案为:.
利用待定系数法可得,然后根据题意可得,从而可得,然后进行计算即可解答.
本题考查了反比例函数的应用,熟练掌握待定系数法求反比例函数解析式是解题的关键.
17.【答案】解:根据与成正比例关系,与成反比例关系,
设,.
则.
把,;,分别代入上式,
得
解得
所以.
当时,
.
【解析】本题考查了待定系数法求函数解析式,根据正比例与反比例关系设出与之间的关系是解题的关键,设关系式时注意正比例与反比例关系的比例系数要区分,不能用同一个字母,这一点也是同学们经常犯的错误.
根据正比例关系与反比例关系设出比例式,然后把两组数据代入关系式,解方程组即可;
把的值代入所求函数关系式,计算即可得解.
18.【答案】解:与成正比例,与成反比例,
,,
,当时,,当时,,
,
,,
;
当,.
【解析】本题考查的是反比例函数及正比例函数的定义,以及待定系数法求函数解析式,解答此题的关键是能根据题意得出与的函数关系式.
先根据题意得出,,根据,当时,,当时,得出、的函数关系式即可;
把代入中的函数关系式,求出的值即可.
19.【答案】解:在面积为定值的一组菱形中,当菱形的一条对角线长为时,它的另一条对角线长为,
,
菱形的两条对角线的长分别为,,
,
关于的函数表达式为:;
这个函数是反比例函数,比例系数是.
其中一个菱形的一条对角线长为,
另一条对角线长为:,
这个菱形的边长为:,
这个菱形的边长.
【解析】此题考查了菱形的性质、反比例函数的概念.掌握菱形的面积等于其对角线积的一半是解题的关键.
由在面积为定值的一组菱形中,当菱形的一条对角线长为时,它的另一条对角线长为,即可得,继而求得答案;
由其中一个菱形的一条对角线长为,可求得另一条对角线长,继而求得答案.
20.【答案】解:把点代入,得,
把代入反比例函数,
;
反比例函数的解析式为;
一次函数的图象与轴交于点,
,
设,
,
,
或,
的坐标为或.
【解析】本题考查了反比例函数与一次函数的交点问题,用待定系数法求出反比例函数的解析式等知识点,能用待定系数法求出反比例函数的解析式是解此题的关键.
利用点在上求,进而代入反比例函数求即可;
设,求得点的坐标,则,然后根据三角形面积公式列出方程,解方程即可.
21.【答案】解:、两点坐标分别代入反比例函数,可得,,
、,
把、代入一次函数,可得
,
解得,
直线的解析式为.
,.
.
从图象看出或时,一次函数图象在反比例函数图象的下方,
当时,的取值范围是:或.
如图,作点关于轴的对称点,连接交轴于点,则的最小值等于的长,
过作轴的平行线,过作轴的平行线,交于点,
则中,,,
的最小值为.
【解析】依据反比例函数的图象交于、两点,即可得到、,代入一次函数,可得直线的解析式,从而求出、两点的坐标即可求出的面积;
当或时,一次函数图象在反比例函数图象的下方,即可得到当时,的取值范围是:或;
作点关于轴的对称点,连接交轴于点,则的最小值等于的长,利用勾股定理即可得到的长.
本题考查的是反比例函数与一次函数的交点问题,根据函数图象的上下位置关系结合交点的横坐标,得出不等式的取值范围是解答此题的关键.
22.【答案】解:直线:与轴交于点,
,
,
一次函数解析式为:,
直线与轴交于点为,
点的坐标为;
双曲线与直线交于,两点,
点在直线上,
当点的横坐标为时,,
点的坐标为,
,
的值为
或.
【解析】
【分析】
本题主要涉及一次函数与反比例函数相交的知识点.根据交点既在一次函数上又在反比例函数上,即可解决问题.
由点的坐标,可求出直线的解析式,再由解析式求出点坐标.
把点的横坐标代入直线解析式即可求得点的纵坐标,然后把点代入反比例函数解析式即可得值.
根据的面积的取值范围求点的横坐标取值,然后把横坐标代入直线解析式,即可求得点纵坐标的取值范围,进而求得的取值范围.
【解答】
解:见答案;
见答案;
如图:当时,
,
,
,
,
;
如图,当时,
,
,
,
,
,
;
或.
23.【答案】解:设电流与电阻之间的函数解析式为,
由图象知,函数的图像过点,
,
解得,
这个反比例函数解析式为;
蓄电池的电压是;
把,,分别代入得:
,,,
,,;
限制电流不能超过,
,
用电器的可变电阻应控制在.
【解析】设电流与电阻之间的函数解析式为,用待定系数法求出解析式即可;
由反比例函数解析式即可得到结论;
把,,分别代入即可求出,,;
由函数解析式即可求出电流不能超过,得出电器的可变电阻应控制范围.
本题考查了反比例函数的应用,求出反比例函数解析式是解决此题的关键.
24.【答案】解:设与的函数关系式为,
把,代入上式,解得.
与的函数关系式为.
当时,.
当气体体积为时,气压是;
由,得,
气球的体积应不小于.
【解析】设与的函数关系式为,将代入即可得出的值,由此可得出结论;
将代入中所求解析式即可得出结论;
由,得,由此可得出结论.
主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用不等式解决实际问题.
25.【答案】解:由表中数据可知,销售单价与日销售量的乘积为定值,
与之间的函数关系为反比例函数,
设与之间的函数关系式为为常数且,
把代入解析式得,,
解得:,
与之间的函数关系式为;
由题意得:,
,
当时,最大,最大值为,
与之间的函数关系式为,当日销售单价定为元时,才能获得最大日销售利润.
【解析】要确定与之间的函数关系式,通过观察表中数据,可以发现与的乘积是相同的,都是,所以可知与成反比例,用待定系数法求解即可;
首先要知道纯利润销售单价日销售数量,这样就可以确定与的函数关系式,然后根据题目的售价最高不超过元个,就可以求出获得最大日销售利润时的日销售单价.
本题考查了反比例函数的定义,两个变量的积是定值,也考查了根据实际问题和反比例函数的关系式求最大值,属于中等难度的题,解答此类题目的关键是仔细理解题意.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
湘教版初中数学九年级上册第一章《反比例函数》单元测试卷
考试范围:第一章;考试时间:120分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分。在每小题列出的选项中,选出符合题目的一项)
下列函数中,是的反比例函数的是( )
A. B. C. D.
如图,长方体的体积是,底面一边长为记底面另一边长为,底面的周长为,长方体的高为当在一定范围内变化时,和都随的变化而变化,则与,与满足的函数关系分别是( )
A. 一次函数关系,二次函数关系
B. 反比例函数关系,二次函数关系
C. 反比例函数关系,一次函数关系
D. 一次函数关系,反比例函数关系
给出的六个关系式:,其中是的反比例函数是( )
A. B. C. D.
若函数是反比例函数,则必须满足( )
A. B.
C. 或 D. 且
已知点、、在反比例函数的图象上,当时,、、的大小关系( )
A. B. C. D.
如图,过双曲线上的动点作轴于点,是直线上的点,且满足,过点作轴的平行线交此双曲线于点如果的面积为,则的值为( )
A. B. C. D.
如图,矩形的边在轴的正半轴上,顶点在反比例函数的图象上,连接并延长交轴于点,且,则的值为( )
A. B. C. D.
如图,在直角坐标系中,以坐标原点,,为顶点的,其两个锐角对应的外角角平分线相交于点,且点恰好在反比例函数的图象上,则点的横坐标为( )
A.
B.
C.
D.
春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物的方式进行消毒在对某宿舍进行消毒的过程中,先经过的集中药物喷洒,再封闭宿舍,然后打开门窗进行通风,室内每立方米空气中含药量与药物在空气中持续时间之间的函数关系如图所示,在打开门窗通风前分别满足两个一次函数关系,在通风后又满足反比例函数关系,则下列说法中错误的是( )
A. 经过集中喷洒药物,室内空气中的含药量最高达到
B. 室内空气中的含药量不低于的持续时间达到了
C. 当室内空气中的含药量不低于且持续时间不低于时,才能有效杀灭某种传染病毒,此次消毒完全有效
D. 当室内空气中的含药量低于时,对人体才是安全的,所以从室内空气中的含药量达到开始,需经过,学生才能进入室内
研究表明近视眼镜的度数度与镜片焦距成反比例已知度近视眼镜镜片的焦距为,则与的函数表达式为( )
A. B. C. D.
某学校要种植一块面积为的长方形草坪,要求两边长均不小于,则草坪的一边长为单位:随另一边长单位:的变化而变化的图象可能是( )
B.
C. D.
某校科技小组进行野外考察,利用铺垫木板的方式,通过了一片烂泥湿地,他们发现,当人和木板对湿地的压力一定时,人和木板对地面的压强随着木板面积的变化而变化,如果人和木板对湿地地面的压力合计,那么下列说法正确的是( )
A. 与的函数表达式为
B. 当越来越大时,也越来越大
C. 若压强不超过时,木板面积最多
D. 当木板面积为时,压强是
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
已知与成反比例,比例系数为,与成正比例,比例系数为,和是已知数,且,则关于成______比例.填“正”或“反”
若与成正比例,与成反比例,与成正比例,与成反比例,则与成______比例.
若点,在反比例函数的图象上,则 ______ 填“”或“”或“”
一辆汽车前灯电路上的电压保持不变,选用灯泡的电阻为,通过的电流强度为,由欧姆定律可知,当电阻为时,测得通过的电流强度为为保证电流强度不低于且不超过,则选用灯泡电阻的取值范围是______.
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
已知,与成正比例函数关系,与成反比例函数关系,且时,;时,.
求与之间的函数表达式;
当时,求的值.
已知,与成正比例,与成反比例.当时,;当时,.求关于的函数表达式;
求当时的值.
在面积为定值的一组菱形中,当菱形的一条对角线长为时,它的另一条对角线长为.
设菱形的两条对角线的长分别为,,求关于的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.
若其中一个菱形的一条对角线长为,求这个菱形的边长.
如图,一次函数的图象与反比例函数在第一象限的图象交于和两点,与轴交于点.
求反比例函数的解析式;
若点在轴上,且的面积为,求点的坐标.
如图,在平面直角坐标中,点是坐标原点,一次函数与反比例函数的图象交于、两点.
求直线的解析式及面积;
根据图象写出当时,的取值范围;
若点在轴上,求的最小值.
在平面直角坐标系中,直线:与轴交于点,与轴交于点双曲线与直线交于,两点,其中点的纵坐标大于点的纵坐标.
求点的坐标;
当点的横坐标为时,求的值;
连接,记的面积为若,结合函数图象,直接写出的取值范围.
已知蓄电池的电压为定值,使用蓄电池时,电流单位:与电阻单位:是反比例函数关系,它的图象如图所示.
请写出这个反比例函数解析式;
蓄电池的电压是多少?
下表中的、、的值分别是多少?
如果以此蓄电池为电源的用电器的限制电流不能超过,那么用电器可变电阻应控制在什么范围?
某气球内充满一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.
写出这个函数的表达式;
当气体体积为时,气压是多少?
当气球内的气压大于时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
受疫情影响,小林为了生计摆地摊,到批发市场进一批单价元的小商品,在夜市营销中统计该批商品的销售单价元与日销售量个之间有如下关系:
猜测并确定与之间的函数关系式;
设经营此小商品的销售利润为元,求出与之间的函数关系式.若物价局规定此小商品的售价最高不能超过元个,请你求出当日销售单价定为多少时,才能获得最大日销售利润?
销售单价元
日销售量个
答案和解析
1.【答案】
【解析】解:如果两个变量、之间的关系可以表示成为常数,的形式,那么称是的反比例函数.
故选:.
根据反比例函数的定义即可求出答案.
本题考查反比例函数的定义,解题的关键是熟练运用反比例函数的定义,本题属于基础题型.
2.【答案】
【解析】解:由底面的周长公式:底面周长长宽,
可得:,
即:.
与的关系为:一次函数关系.
根据长方体的体积公式:长方体体积长宽高,
可得:,
,
与的关系为:反比例函数关系.
故选:.
根据底面的周长公式“底面周长长宽“可表示出与的关系式,根据长方体的体积公式“长方体体积长宽高”可表示出与,根据各自的表达式形式判断函数类型即可.
此题考查了函数关系式的综合应用,涉及到一次函数,二次函数,反比例函数等知识,熟知函数的相关类型并能够根据实际问题列出函数关系式是解决本题的关键.
3.【答案】
【解析】略
4.【答案】
【解析】略
5.【答案】
【解析】解:反比例函数的图象在二四象限,在每个象限内随的增大而增大,
又
点和在第二象限、而在第四象限,
于是有:,而,
因此,
故选:.
在反比例函数的图象在二四象限,根据,可以确定点、、所在象限,根据反比例函数的图象和性质,可以确定、、的大小关系.
考查反比例函数的图象和性质,即函数的增减性.
6.【答案】
【解析】解:设点的坐标为,
,轴,
点的坐标为,
,
的面积为,
,
解得,.
故选:.
设点的坐标为,由确定点的坐标,根据的面积为,列等式可解答.
本题考查的是反比例函数图象上点的坐标特征,根据坐标表示出线段的长度是解题的关键.
7.【答案】
【解析】解:双曲线经过点,
设,
则,,
矩形,
,
,
,.
∽.
,
.
.
.
.
.
故选:.
先用含的代数式表示的面积,再求.
本题考查求反比例的,通过相似三角形边的关系将三角形的面积用含的代数式表示是求解本题的关键.
8.【答案】
【解析】解:如图,过点分别作轴,轴,的垂线,垂足分别为、、,
、分别是两锐角相应的外角平分线,
,
四边形是正方形,
由角平分线的对称性可知,,,
在中,,
设,则,,
由于得,
,
解得,
即,
,
故选:.
根据角平分线的性质可得,进而得出四边形是正方形,由角平分线的对称性得出,,由勾股定理求出,设,列方程求出的值,进而确定点的横坐标.
本题考查反比例函数图象上点的坐标特征,角平分线的性质以及直角三角形的性质,掌握反比例函数图象上点的坐标特征以及勾股定理是解决问题的前提.
9.【答案】
【解析】解:由已知得,
当时,函数解析式为
当时,函数解析式为
当时,函数解析式为.
由题图知,选项不符合题意
当时,或,
室内空气中的含药量不低于的持续时间达到了,
故B选项不符合题意
当时,或,,
故C选项符合题意
当时,或,,
从室内空气中的含药量达到开始,
需经过,学生才能进入室内,
故D选项不符合题意.
综上,选C.
故选C.
10.【答案】
【解析】
【分析】
本题考查了根据实际问题列反比例函数关系式,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.反比例函数的一般形式为是常数,且,常用待定系数法求解函数解析式设出反比例函数解析式,把代入即可求解.
【解答】
解:设,
度近视眼镜镜片的焦距为,
即,,
,
.
故选C.
11.【答案】
【解析】
【分析】
本题考查反比例函数的图象,反比例函数的应用,根据反比例函数解析式确定的取值范围,即可求得的取值范围,熟练掌握实际问题的反比例函数图象是解题的关键,易知是的反比例函数,再根据边长的取值范围即可解题.
【解答】
解:草坪面积为,
、存在关系,
两边长均不小于,
当时,,
又,
符合条件的是图.
故选C.
12.【答案】
【解析】解:压力一定时,压强和受力面积成反比;
,
,
是的反比例函数,
,
当越来越大时,也越来越小,
故选项A,不符合题意;
当时,
即,
,
若压强不超过时,木板面积最少,
故选项C不符合题意;
当时,,
当木板面积为时,压强是,
故选项D符合题意;
故选:.
压力一定时,压强和受力面积成反比,根据压力为写出解析式,根据解析式即可判定各个选项.
本题考查反比例函数的应用,根据题意写出反比例函数的解析式是解题的关键.
13.【答案】反
【解析】解:与成反比例,比例系数为,
,
与成正比例,比例系数为,
,
,
和是已知数,且,
关于成反比例,
故答案为:反.
根据反比例函数的定义得出,根据正比例函数的定义得出,求出,再根据反比例函数的定义得出答案即可.
本题考查了正比例函数与反比例函数的定义,能熟记正比例函数与反比例函数的定义是解此题的关键.
14.【答案】反
【解析】解:与成正比例,与成反比例,与成正比例,与成反比例,
,,
,
与成反比例,
同理可得:与成反比例,与成正比例,与成正比例,
与成反比例,
比例关系每四个一循环,分别是:正比例,反比例,反比例,正比例关系,
,
与成反比例关系,
故答案为:反.
根据与成正比例,与成反比例,得出,,即可得出,进而得出与成反比例,与成正比例,与成正比例,进而得出与比例关系每四个一循环,进而得出答案.
此题主要考查了正比例函数与反比例函数的关系,利用已知得出与比例关系,每四个一循环是解题关键.
15.【答案】
【解析】解:,
反比例函数的图象在一、三象限,且在每个象限内随的增大而减小,
点,同在第三象限,且,
,
故答案为.
反比例函数的图象在一、三象限,在每个象限内,随的增大而减小,判断出的值的大小关系.
本题考查反比例函数的图象和性质,掌握反比例函数的增减性是解决问题的关键,
16.【答案】
【解析】解:由题意得:
,
当电阻为时,测得通过的电流强度为,
,
,
当时,
,
,
故答案为:.
利用待定系数法可得,然后根据题意可得,从而可得,然后进行计算即可解答.
本题考查了反比例函数的应用,熟练掌握待定系数法求反比例函数解析式是解题的关键.
17.【答案】解:根据与成正比例关系,与成反比例关系,
设,.
则.
把,;,分别代入上式,
得
解得
所以.
当时,
.
【解析】本题考查了待定系数法求函数解析式,根据正比例与反比例关系设出与之间的关系是解题的关键,设关系式时注意正比例与反比例关系的比例系数要区分,不能用同一个字母,这一点也是同学们经常犯的错误.
根据正比例关系与反比例关系设出比例式,然后把两组数据代入关系式,解方程组即可;
把的值代入所求函数关系式,计算即可得解.
18.【答案】解:与成正比例,与成反比例,
,,
,当时,,当时,,
,
,,
;
当,.
【解析】本题考查的是反比例函数及正比例函数的定义,以及待定系数法求函数解析式,解答此题的关键是能根据题意得出与的函数关系式.
先根据题意得出,,根据,当时,,当时,得出、的函数关系式即可;
把代入中的函数关系式,求出的值即可.
19.【答案】解:在面积为定值的一组菱形中,当菱形的一条对角线长为时,它的另一条对角线长为,
,
菱形的两条对角线的长分别为,,
,
关于的函数表达式为:;
这个函数是反比例函数,比例系数是.
其中一个菱形的一条对角线长为,
另一条对角线长为:,
这个菱形的边长为:,
这个菱形的边长.
【解析】此题考查了菱形的性质、反比例函数的概念.掌握菱形的面积等于其对角线积的一半是解题的关键.
由在面积为定值的一组菱形中,当菱形的一条对角线长为时,它的另一条对角线长为,即可得,继而求得答案;
由其中一个菱形的一条对角线长为,可求得另一条对角线长,继而求得答案.
20.【答案】解:把点代入,得,
把代入反比例函数,
;
反比例函数的解析式为;
一次函数的图象与轴交于点,
,
设,
,
,
或,
的坐标为或.
【解析】本题考查了反比例函数与一次函数的交点问题,用待定系数法求出反比例函数的解析式等知识点,能用待定系数法求出反比例函数的解析式是解此题的关键.
利用点在上求,进而代入反比例函数求即可;
设,求得点的坐标,则,然后根据三角形面积公式列出方程,解方程即可.
21.【答案】解:、两点坐标分别代入反比例函数,可得,,
、,
把、代入一次函数,可得
,
解得,
直线的解析式为.
,.
.
从图象看出或时,一次函数图象在反比例函数图象的下方,
当时,的取值范围是:或.
如图,作点关于轴的对称点,连接交轴于点,则的最小值等于的长,
过作轴的平行线,过作轴的平行线,交于点,
则中,,,
的最小值为.
【解析】依据反比例函数的图象交于、两点,即可得到、,代入一次函数,可得直线的解析式,从而求出、两点的坐标即可求出的面积;
当或时,一次函数图象在反比例函数图象的下方,即可得到当时,的取值范围是:或;
作点关于轴的对称点,连接交轴于点,则的最小值等于的长,利用勾股定理即可得到的长.
本题考查的是反比例函数与一次函数的交点问题,根据函数图象的上下位置关系结合交点的横坐标,得出不等式的取值范围是解答此题的关键.
22.【答案】解:直线:与轴交于点,
,
,
一次函数解析式为:,
直线与轴交于点为,
点的坐标为;
双曲线与直线交于,两点,
点在直线上,
当点的横坐标为时,,
点的坐标为,
,
的值为
或.
【解析】
【分析】
本题主要涉及一次函数与反比例函数相交的知识点.根据交点既在一次函数上又在反比例函数上,即可解决问题.
由点的坐标,可求出直线的解析式,再由解析式求出点坐标.
把点的横坐标代入直线解析式即可求得点的纵坐标,然后把点代入反比例函数解析式即可得值.
根据的面积的取值范围求点的横坐标取值,然后把横坐标代入直线解析式,即可求得点纵坐标的取值范围,进而求得的取值范围.
【解答】
解:见答案;
见答案;
如图:当时,
,
,
,
,
;
如图,当时,
,
,
,
,
,
;
或.
23.【答案】解:设电流与电阻之间的函数解析式为,
由图象知,函数的图像过点,
,
解得,
这个反比例函数解析式为;
蓄电池的电压是;
把,,分别代入得:
,,,
,,;
限制电流不能超过,
,
用电器的可变电阻应控制在.
【解析】设电流与电阻之间的函数解析式为,用待定系数法求出解析式即可;
由反比例函数解析式即可得到结论;
把,,分别代入即可求出,,;
由函数解析式即可求出电流不能超过,得出电器的可变电阻应控制范围.
本题考查了反比例函数的应用,求出反比例函数解析式是解决此题的关键.
24.【答案】解:设与的函数关系式为,
把,代入上式,解得.
与的函数关系式为.
当时,.
当气体体积为时,气压是;
由,得,
气球的体积应不小于.
【解析】设与的函数关系式为,将代入即可得出的值,由此可得出结论;
将代入中所求解析式即可得出结论;
由,得,由此可得出结论.
主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式.会用不等式解决实际问题.
25.【答案】解:由表中数据可知,销售单价与日销售量的乘积为定值,
与之间的函数关系为反比例函数,
设与之间的函数关系式为为常数且,
把代入解析式得,,
解得:,
与之间的函数关系式为;
由题意得:,
,
当时,最大,最大值为,
与之间的函数关系式为,当日销售单价定为元时,才能获得最大日销售利润.
【解析】要确定与之间的函数关系式,通过观察表中数据,可以发现与的乘积是相同的,都是,所以可知与成反比例,用待定系数法求解即可;
首先要知道纯利润销售单价日销售数量,这样就可以确定与的函数关系式,然后根据题目的售价最高不超过元个,就可以求出获得最大日销售利润时的日销售单价.
本题考查了反比例函数的定义,两个变量的积是定值,也考查了根据实际问题和反比例函数的关系式求最大值,属于中等难度的题,解答此类题目的关键是仔细理解题意.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
