湖南省长沙市三年(2020-2022)小升初数学卷真题分题型分层汇编-14解答题(人教版)(含答案)
文档属性
| 名称 | 湖南省长沙市三年(2020-2022)小升初数学卷真题分题型分层汇编-14解答题(人教版)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 452.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 12:30:46 | ||
图片预览


文档简介
湖南省长沙市三年(2020-2022)小升初数学卷真题分题型分层汇编
14解答题
负数的意义及其应用(共1小题)
(2020 长沙)把几个数用大括号括起来,中间用逗号断开,如:{1,2,8}、{﹣2,7,,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数10﹣a也必是这个集合的元素,这样的集合我们称为“好的集合”.例如集合{10,0}就是一个“好的集合”.
(1)集合{﹣2,7,,19} (填“是”或“不是”)“好的集合”.
(2)请你再写出两个“好的集合”(不得与上面出现过的集合重复).
(3)在所有“好的集合”中,元素个数最少的集合是 .
“式”的规律(共1小题)
(2020 岳麓区)观察1+3=4;4+5=9;9+7=16;16+9=25;25+11=36这五道算式,找出规律,然后填写20012+ =20022.
简单周期现象中的规律(共1小题)
(2020 长沙)有同样大小的红、蓝、白玻璃球共76个,始终按2个红球、3个蓝球,4个白球的顺序排列.蓝玻璃球的个数占总数的.
圆与组合图形(共1小题)
(2020 长沙)图中是一个边长为4厘米的正方形,那么总的阴影面积是多少平方厘米?(π取3.14)
简单的立方体切拼问题(共1小题)
(2020 长沙)有n个同样大小的正方体,将它们摞成一个长方体,这个长方体的底面就是原正方体的底面.如果这个长方体的表面积是3096平方厘米,当从这个长方体的顶部拿去一个正方体后,新的长方体的表面积比原来长方体的表面积减少144平方厘米,那么n是多少?(写出简要解答步骤)
多边形的内角和(共1小题)
(2020 岳麓区)同学们都知道三角形内角和是180°,四边形内角和是360°,请你求出99边形的内角和。
组合图形的面积(共6小题)
(2022 长沙)如图,四边形ABCD是周长为80cm的正方形,在以C为圆心、CD为半径的扇形中,∠DCE=90°。求阴影部分的面积。(圆周率取3.14)
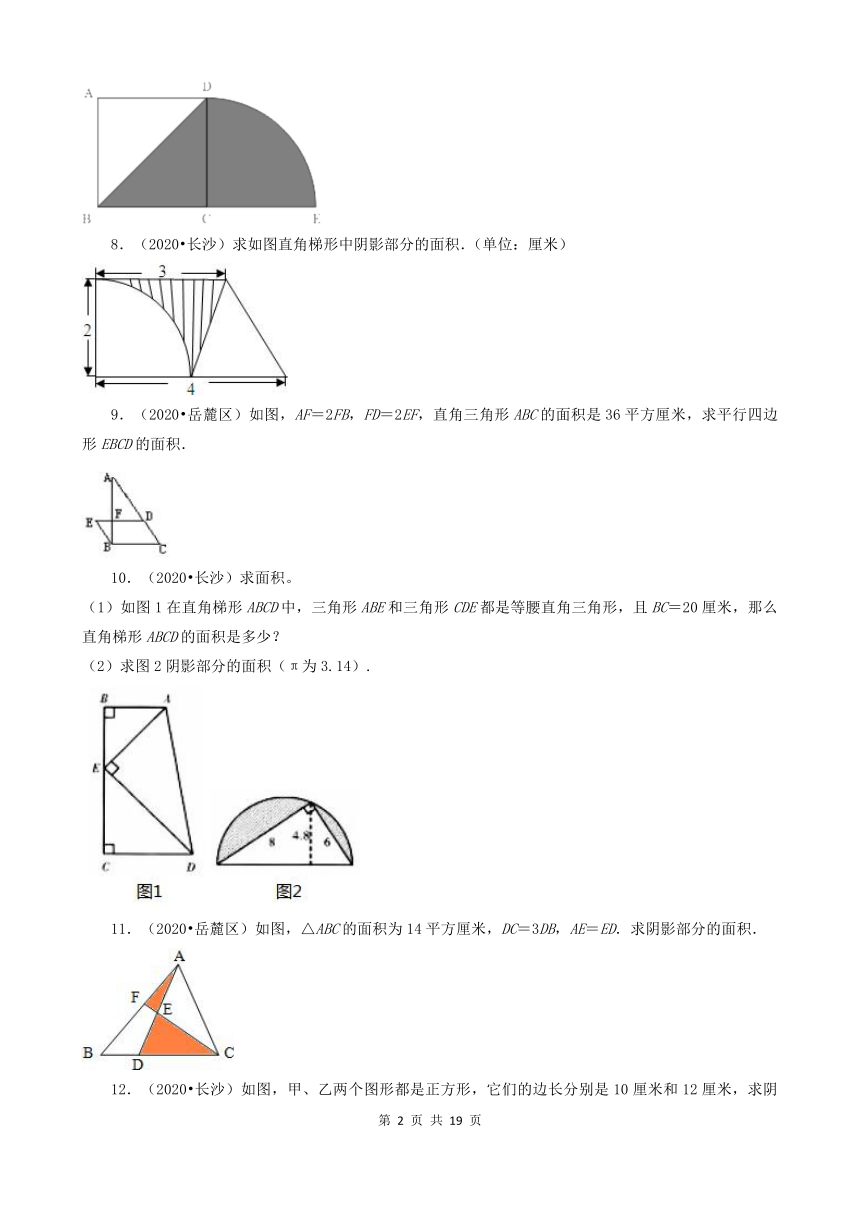
(2020 长沙)求如图直角梯形中阴影部分的面积.(单位:厘米)
(2020 岳麓区)如图,AF=2FB,FD=2EF,直角三角形ABC的面积是36平方厘米,求平行四边形EBCD的面积.
(2020 长沙)求面积。
(1)如图1在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是多少?
(2)求图2阴影部分的面积(π为3.14).
(2020 岳麓区)如图,△ABC的面积为14平方厘米,DC=3DB,AE=ED.求阴影部分的面积.
(2020 长沙)如图,甲、乙两个图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积.
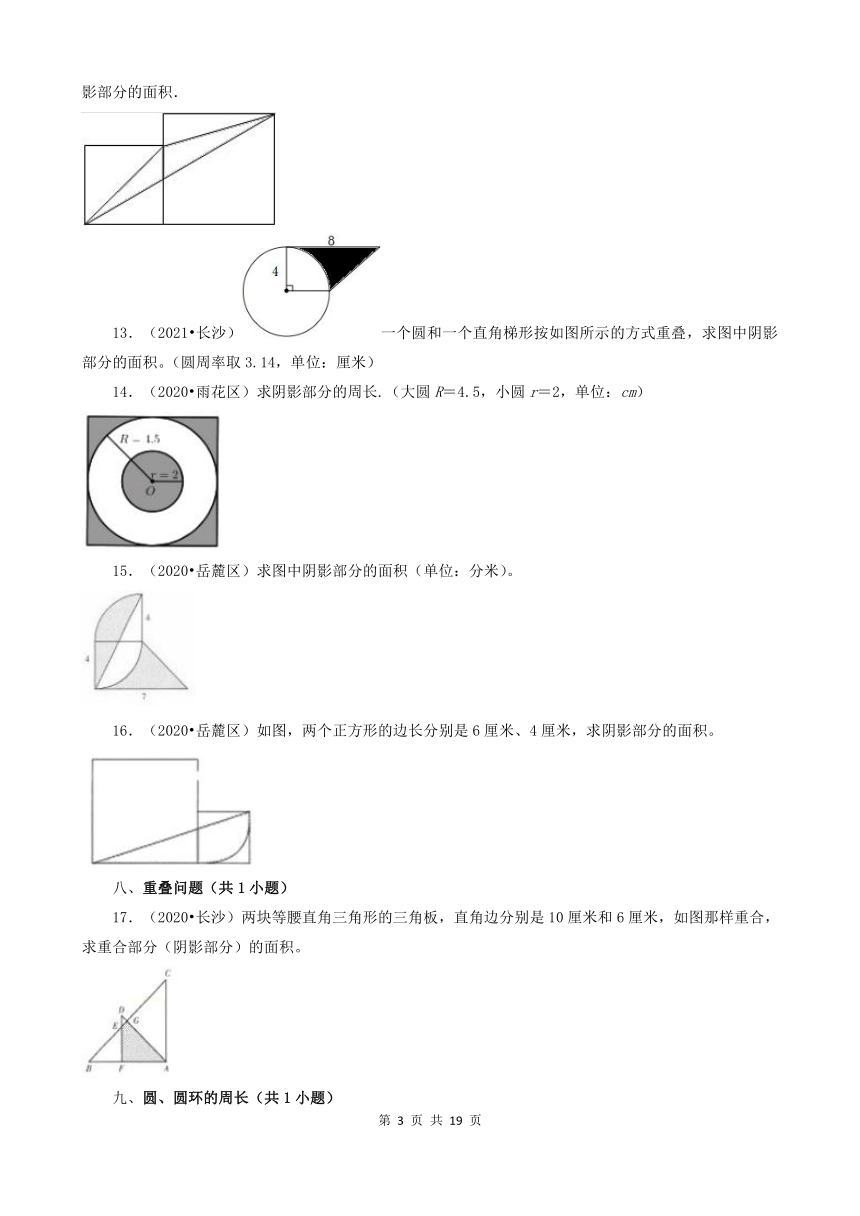
(2021 长沙)一个圆和一个直角梯形按如图所示的方式重叠,求图中阴影部分的面积。(圆周率取3.14,单位:厘米)
(2020 雨花区)求阴影部分的周长.(大圆R=4.5,小圆r=2,单位:cm)
(2020 岳麓区)求图中阴影部分的面积(单位:分米)。
(2020 岳麓区)如图,两个正方形的边长分别是6厘米、4厘米,求阴影部分的面积。
重叠问题(共1小题)
(2020 长沙)两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米,如图那样重合,求重合部分(阴影部分)的面积。
圆、圆环的周长(共1小题)
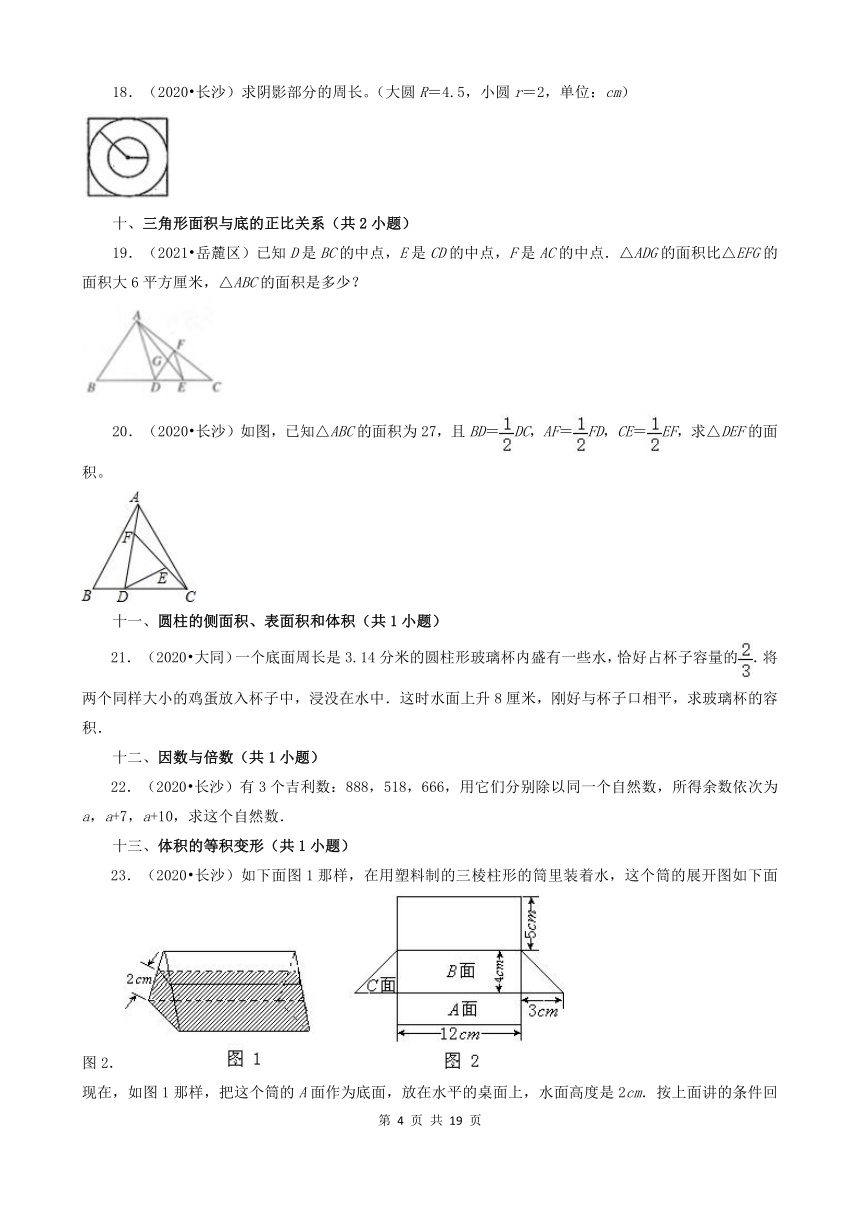
(2020 长沙)求阴影部分的周长。(大圆R=4.5,小圆r=2,单位:cm)
三角形面积与底的正比关系(共2小题)
(2021 岳麓区)已知D是BC的中点,E是CD的中点,F是AC的中点.△ADG的面积比△EFG的面积大6平方厘米,△ABC的面积是多少?
(2020 长沙)如图,已知△ABC的面积为27,且BD=DC,AF=FD,CE=EF,求△DEF的面积。
圆柱的侧面积、表面积和体积(共1小题)
(2020 大同)一个底面周长是3.14分米的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的.将两个同样大小的鸡蛋放入杯子中,浸没在水中.这时水面上升8厘米,刚好与杯子口相平,求玻璃杯的容积.
因数与倍数(共1小题)
(2020 长沙)有3个吉利数:888,518,666,用它们分别除以同一个自然数,所得余数依次为a,a+7,a+10,求这个自然数.
体积的等积变形(共1小题)
(2020 长沙)如下面图1那样,在用塑料制的三棱柱形的筒里装着水,这个筒的展开图如下面图2.
现在,如图1那样,把这个筒的A面作为底面,放在水平的桌面上,水面高度是2cm.按上面讲的条件回答下列问题:
(1)把B面作为底面,放在水平的桌面上,水面高多少厘米?
(2)把C面(直角三角形的面)作为底面,放在水平的桌面上,水面高又是多少厘米?
逻辑推理(共1小题)
(2020 岳麓区)张凯靓、王全美、余鑫盈三位老师共同担任五(2)班的语文、数学、英语、音乐、美术和体育六门课的教学,每人教两门,现在知道:
(1)英语老师和数学老师是邻居;
(2)王全美年纪最小;
(3)张凯靓喜欢和体育老师、数学老师来往;
(4)体育老师比语文老师年龄大;
(5)王全美、语文老师、音乐老师三人经常一起做操。
请判断各人分别教的是哪两门课程.
列方程解含有两个未知数的应用(共2小题)
(2020 岳麓区)原来每个足球的价钱是每个篮球价钱的,每个足球和每个篮球的售价都提高3元后,每个足球的价钱是每个篮球价钱的,现在每个篮球售价 元.
(2020 岳麓区)一串数有11个数,中间一个数最大.从中间的数往前数,一个数比一个数小2;从中间的数往后数,一个数比一个数小3,这11个数的总和是200,那么中间的数是多少?
比的应用(共4小题)
(2021 长沙)有A、B两棵小树,现在高度均为80cm。A、B两棵树的生长速度之比为12:7。
(1)当A树长到104厘米高时,B树有多高?
(2)当A、B两树的高度之比为4:3时,A树高 厘米。(直接填出得数)
(2020 长沙)图书馆共进两批图书,第一批图书本数比第二批多10%,如果从第一批拿80本到第二批,这时第一批本数与第二批本数之比是3:4,图书馆这两批图书共进了多少本?
(2020 长沙)甲、乙两个班的学生人数的比是5:4,如果从乙班转走9名学生,那么甲班就比乙班人数多.这时乙班有多少人?
(2020 岳麓区)六年级一班原有学生42人,其中男生占.后来转来女生若干人,这时男生与女生人数的比是6:5.现在全班有多少人?
比的意义(共1小题)
(2020 岳麓区)甲、乙、丙三个数,已知甲:(乙+丙)=4:3,乙:丙=2:7,求甲:乙:丙.
含字母式子的求值(共1小题)
(2020 岳麓区)已知==20092010,求.
参考答案与试题解析
负数的意义及其应用(共1小题)
(2020 长沙)把几个数用大括号括起来,中间用逗号断开,如:{1,2,8}、{﹣2,7,,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数10﹣a也必是这个集合的元素,这样的集合我们称为“好的集合”.例如集合{10,0}就是一个“好的集合”.
(1)集合{﹣2,7,,19} 不是 (填“是”或“不是”)“好的集合”.
(2)请你再写出两个“好的集合”(不得与上面出现过的集合重复).
(3)在所有“好的集合”中,元素个数最少的集合是 {5} .
【解答】解:(1)集合{﹣2,7,,19}不是“好的集合”。
(2){3,7},{1,9}。
(3)在所有“好的集合”中,元素个数最少的集合是{5}。
故答案为:不是;{5}。
“式”的规律(共1小题)
(2020 岳麓区)观察1+3=4;4+5=9;9+7=16;16+9=25;25+11=36这五道算式,找出规律,然后填写20012+ 4003 =20022.
【解答】解:通过观察可以得出规律:相邻的两个自然数的平方差,得到的差等于这两个自然数的和.
20022﹣20012
=2002+2001
=4003
所以:20012+4003=20022.
故答案为:4003.
简单周期现象中的规律(共1小题)
(2020 长沙)有同样大小的红、蓝、白玻璃球共76个,始终按2个红球、3个蓝球,4个白球的顺序排列.蓝玻璃球的个数占总数的.
【解答】解:76÷9=8…4,
所以76个球共经历了8个周期零4个球,
所以蓝球的个数为:8×3+2=26(个),
26÷76=
答:蓝玻璃球的个数占总数的.
故答案为:.
圆与组合图形(共1小题)
(2020 长沙)图中是一个边长为4厘米的正方形,那么总的阴影面积是多少平方厘米?(π取3.14)
【解答】解:4÷2=2(厘米)
3.14×22÷2+4×4÷4
=6.28+4
=10.28(平方厘米)
答:总的阴影面积是10.28平方厘米。
简单的立方体切拼问题(共1小题)
(2020 长沙)有n个同样大小的正方体,将它们摞成一个长方体,这个长方体的底面就是原正方体的底面.如果这个长方体的表面积是3096平方厘米,当从这个长方体的顶部拿去一个正方体后,新的长方体的表面积比原来长方体的表面积减少144平方厘米,那么n是多少?(写出简要解答步骤)
【解答】解:正方体一个面的面积是:144÷4=36(平方厘米),根据长方体的表面积可得:
36×(4n+2)=3096,
144n+72=3096,
144n=3024,
n=21,
答:n是21.
多边形的内角和(共1小题)
(2020 岳麓区)同学们都知道三角形内角和是180°,四边形内角和是360°,请你求出99边形的内角和。
【解答】解:从四边形的一个顶点可以引出1条对角线,把四边形分成2个三角形,那么它的内角和是180°×2=360°,
从五边形的一个顶点可以引出2条对角线,把五边形分成3个三角形,那么它的内角和是180°×3=540°,
从六边形的一个顶点可以引出3条对角线,把六边形分成4个三角形,那么它的内角和是180°×4=720°,
…
从n(n大于或等于3)边形的一个顶点可以引出(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,那么n边形的内角和为180°×(n﹣2),
当n=99时,
180°×(99﹣2)
=180°×97
=17460°
答:99边形的内角和是17460°。
组合图形的面积(共6小题)
(2022 长沙)如图,四边形ABCD是周长为80cm的正方形,在以C为圆心、CD为半径的扇形中,∠DCE=90°。求阴影部分的面积。(圆周率取3.14)
【解答】解:正方形的边长为:80÷4=20(cm)
20×20÷2+3.14×202÷4
=400÷2+3.14×400÷4
=200+314
=514(平方厘米)
答:阴影部分的面积是514平方厘米。
(2020 长沙)求如图直角梯形中阴影部分的面积.(单位:厘米)
【解答】解:(3+4)×2÷2﹣3.14×22×﹣(4﹣2)×2÷2,
=7﹣3.14﹣2,
=1.86(平方厘米);
答:阴影部分的面积是1.86平方厘米.
(2020 岳麓区)如图,AF=2FB,FD=2EF,直角三角形ABC的面积是36平方厘米,求平行四边形EBCD的面积.
【解答】解:根据题意得出:
BC×3FB÷2=36
FB=36×2÷3÷BC
平行四边形EBCD的面积
BC×FB
=BC×(36×2÷3÷BC)
=36×2÷3
=24(平方厘米)
答:平行四边形EBCD的面积是24平方厘米.
(2020 长沙)求面积。
(1)如图1在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是多少?
(2)求图2阴影部分的面积(π为3.14).
【解答】解:(1)20×20÷2=200(平方厘米)
答:梯形ABCD的面积是200平方厘米。
(2)×3.14×(8×6÷4.8÷2)2﹣8×6÷2
=×3.14×25﹣24
=39.25﹣24
=15.25
答:阴影部分的面积是15.25。
(2020 岳麓区)如图,△ABC的面积为14平方厘米,DC=3DB,AE=ED.求阴影部分的面积.
【解答】解:连接DF,
因为AE=DE,
所以S△AFE=S△DFE,S△ACE=S△DCE.
所以S△ACF=S△DCF.
又因为CD=3DB,
所以S△ACF=S△DCF=3S△BDF;
所以S△ABC=S△BDF×7=14,
故S△BDF=14÷7=2(平方厘米).
S阴影=S△DCF=S△BDF×3=2×3=6(平方厘米).
答:阴影部分的总面积是6平方厘米.
(2020 长沙)如图,甲、乙两个图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积.
【解答】解:12×12+10×10﹣(12+10)×12÷2﹣10×10÷2﹣(12﹣10)×12÷2
=144+100﹣132﹣50﹣12
=244﹣194
=50(平方厘米)
答:阴影部分的面积是50平方厘米.
53.(2021 长沙)一个圆和一个直角梯形按如图所示的方式重叠,求图中阴影部分的面积。(圆周率取3.14,单位:厘米)
【解答】解:(4+8)×4÷2﹣3.14×4×4×
=24﹣12.56
=11.44(平方厘米)
答:图中阴影部分的面积是11.44平方厘米。
54.(2020 雨花区)求阴影部分的周长.(大圆R=4.5,小圆r=2,单位:cm)
【解答】解:(4.5×2)×4+2×3.14×4.5+2×3.14×2
=9×4+28.26+12.56
=36+28.26+12.56
=76.82(厘米)
答:阴影部分的周长是76.82厘米。
55.(2020 岳麓区)求图中阴影部分的面积(单位:分米)。
【解答】解:如图:
7×4÷2+4×4÷2
=28÷2+16÷2
=14+8
=22(平方分米)
答:阴影部分的面积是22平方分米。
56.(2020 岳麓区)如图,两个正方形的边长分别是6厘米、4厘米,求阴影部分的面积。
【解答】解:如图分割:
S阴影=S三角形+S弓形
=×6×4+(×3.14×4×4﹣×4×4)
=3×4+(3.14×4﹣2×4)
=12+(12.56﹣8)
=12+12.56﹣8
=16.56(cm2)
答:阴影部分的面积为16.56平方厘米。
重叠问题(共1小题)
51.(2020 长沙)两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米,如图那样重合,求重合部分(阴影部分)的面积。
【解答】解:根据题干分析可得:
10×10÷2÷2﹣(10﹣6)×(10﹣6)÷2
=25﹣4×4÷2
=25﹣8
=17(平方厘米)
答:阴影部分的面积是17平方厘米。
圆、圆环的周长(共1小题)
52.(2020 长沙)求阴影部分的周长。(大圆R=4.5,小圆r=2,单位:cm)
【解答】解:4.5×2×4+2×3.14×4.5+2×3.14×2
=9×4+28.26+12.56
=36+28.26+12.56
=76.82(厘米)
答:阴影部分的周长是76.82厘米。
三角形面积与底的正比关系(共2小题)
58.(2021 岳麓区)已知D是BC的中点,E是CD的中点,F是AC的中点.△ADG的面积比△EFG的面积大6平方厘米,△ABC的面积是多少?
【解答】解:根据题干和图形可得:因为△ADG的面积﹣△EFG的面积=6平方厘米,
所以三角形ADE的面积﹣三角形FDE的面积=6平方厘米,
因为D是BC的中点,E是CD的中点,F是AC的中点,
所以三角形ADE的面积=三角形ADC的面积=三角形ABC的面积;
三角形FDE的面积=三角形FDC的面积=三角形ADC的面积=三角形ABC的面积,
所以三角形ABC的面积﹣三角形ABC的面积=6平方厘米,
即三角形ABC的面积=6平方厘米,
所以三角形ABC的面积为:6÷=48(平方厘米),
答:三角形ABC的面积是48平方厘米.
59.(2020 长沙)如图,已知△ABC的面积为27,且BD=DC,AF=FD,CE=EF,求△DEF的面积。
【解答】解:根据BD=DC,AF=FD,CE=EF,
可知,CD=BC,DF=AD,EF=CF;
△ABC与△ADC等高,底CD=BC,
所以,S△ACD=S△ABC×,
同理可得:S△CDF=S△ACD,S△DEF=S△CDF,
所以,S△DEF=××S△ABC
=×27
=8
答:△DEF的面积为8。
圆柱的侧面积、表面积和体积(共1小题)
(2020 大同)一个底面周长是3.14分米的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的.将两个同样大小的鸡蛋放入杯子中,浸没在水中.这时水面上升8厘米,刚好与杯子口相平,求玻璃杯的容积.
【解答】解:杯子高是:
8÷(1﹣)
=8
=8×3
=24(厘米);
3.14分米=31.4厘米,
3.14×(31.4÷3.14÷2)2×24
=3.14×52×24
=3.14×25×24
=1884(立方厘米);
答:玻璃杯子的容积是1884立方厘米.
因数与倍数(共1小题)
(2020 长沙)有3个吉利数:888,518,666,用它们分别除以同一个自然数,所得余数依次为a,a+7,a+10,求这个自然数.
【解答】解:518﹣7=511,666﹣10=656;888,511,656除以这个数,余数相同;888﹣511=377,888﹣656=232,这个数为377与232的公因数,且大于10,
因为377=13×29,232=8×29,所以这个自然数为29;
答:这个自然数是29.
体积的等积变形(共1小题)
(2020 长沙)如下面图1那样,在用塑料制的三棱柱形的筒里装着水,这个筒的展开图如下面图2.
现在,如图1那样,把这个筒的A面作为底面,放在水平的桌面上,水面高度是2cm.按上面讲的条件回答下列问题:
(1)把B面作为底面,放在水平的桌面上,水面高多少厘米?
(2)把C面(直角三角形的面)作为底面,放在水平的桌面上,水面高又是多少厘米?
【解答】解:在图中标上字母如下图所示,
因X是MN的中点,故Y也是MP的中点,△MXY,△MNP都是直角三角形;
利用勾股定理,可求出XY=1.5cm,水的体积为:
(1.5+3)×2÷2×12=54(cm3);
当YZ与PN垂直,交NP于Z时,XY=NZ=ZP=1.5cm,XN=YZ=2cm;
故三角形XYM与三角形YZP完全一样.
(1)当B作底面时,侧面PMN如下图所示,
因为△YZM与△XYP完全一样.故水深1.5cm.
(2)因高=体积÷底面积,
所以△NMP面积:3×4÷2=6(cm2);
高为:54÷6=9(cm).
答:把B面作为底面,水面高1.5厘米;把C面作为底面,水面高是9厘米.
逻辑推理(共1小题)
(2020 岳麓区)张凯靓、王全美、余鑫盈三位老师共同担任五(2)班的语文、数学、英语、音乐、美术和体育六门课的教学,每人教两门,现在知道:
(1)英语老师和数学老师是邻居;
(2)王全美年纪最小;
(3)张凯靓喜欢和体育老师、数学老师来往;
(4)体育老师比语文老师年龄大;
(5)王全美、语文老师、音乐老师三人经常一起做操。
请判断各人分别教的是哪两门课程.
【解答】解:根据题意知:
(1)英语老师和数学老师不是一个人;
(2)王全美老师最年轻;
(3)张凯靓老师不是体育老师,也不是数学老师,而且体育老师和数学老师不是一个人;
(4)王全美不是体育老师;
(5)王全美老师不是语文老师,也不是音乐老师,而且音乐老师和语文老师是两个人。
综合条件(3)(4)可知,体育老师是余鑫盈老师,数学老师是王全美老师。由条件(5)可知,王全美老师不是音乐老师和语文老师,语文老师是张凯靓老师;所以音乐老师是谁时不能确定;由于英语老师和数学老师是邻居,所以英语老师不是王全美老师,而王全美老师只能是美术老师;由于王全美老师与音乐老师和语文老师经常一起做操,所以张凯靓老师教语文不教音乐,所以音乐老师是余鑫盈老师;张凯靓老师是英语老师。
答:张凯靓老师教语文和英语;王全美老师教数学和美术;余鑫盈老师教体育和音乐。
列方程解含有两个未知数的应用(共2小题)
(2020 岳麓区)原来每个足球的价钱是每个篮球价钱的,每个足球和每个篮球的售价都提高3元后,每个足球的价钱是每个篮球价钱的,现在每个篮球售价 57 元.
【解答】解:设原来每个篮球的价钱是x元,则原来每个足球的价钱是x元,
x+3=(x+3)×
x+3=x+
x+3﹣x=x+﹣x
x+=3
x+﹣=3﹣
x=
x÷=÷
x=54
54+3=57(元)
答:现在每个篮球售价57元.
故答案为:57.
(2020 岳麓区)一串数有11个数,中间一个数最大.从中间的数往前数,一个数比一个数小2;从中间的数往后数,一个数比一个数小3,这11个数的总和是200,那么中间的数是多少?
【解答】解:设中间的数是x,则这11个数依次是:x﹣10,x﹣8,x﹣6,x﹣4,x﹣2,x,x﹣3,x﹣6,x﹣9,x﹣12,x﹣15,可得方程:
11x﹣(2+4+6+8+10)﹣(3+6+9+12+15)=200,
11x=200+30+45,
x=25.
答:中间的数是25.
比的应用(共4小题)
(2021 长沙)有A、B两棵小树,现在高度均为80cm。A、B两棵树的生长速度之比为12:7。
(1)当A树长到104厘米高时,B树有多高?
(2)当A、B两树的高度之比为4:3时,A树高 200 厘米。(直接填出得数)
【解答】解:(1)(104﹣80)×+80
=24×+80
=14+80
=94(厘米)
答:B树有94厘米高。
(2)设A树长12x厘米,则B树长7x厘米。
(80+12x):(80+7x)=4:3
3(80+12x)=4(80+7x)
240+36x=320+28x
36x﹣28x=320﹣240
8x=80
x=10
80+12×10
=80+120
=200(厘米)
答:A树高200厘米。
故答案为:200。
(2020 长沙)图书馆共进两批图书,第一批图书本数比第二批多10%,如果从第一批拿80本到第二批,这时第一批本数与第二批本数之比是3:4,图书馆这两批图书共进了多少本?
【解答】解:设第二批进了x本,则第一批进了(1+10%)x本,根据从第一批拿80本到第二批.由题意
=
=
(1.1x﹣80)×4=(x+80)×3
4.4x﹣320=3x+240
4.4x﹣320+320﹣3x=3x+240+320﹣3x
1.4x=560
1.4x÷1.4=560÷1.4
x=400
400×(1+10)+400
=400×1.1+400
=440+400
=840(本)
答:图书馆这两批图书共进了840本.
(2020 长沙)甲、乙两个班的学生人数的比是5:4,如果从乙班转走9名学生,那么甲班就比乙班人数多.这时乙班有多少人?
【解答】解:甲班比乙班多,
此时乙班学生占3份,甲班学生就是这样的3+2=5(份)
由于甲班份数刚好没有变,所以乙班转走的9名同学刚好是4﹣3=1(份)
所以这时乙班人数是:9×3=27(人)
答:这时乙班有27人.
(2020 岳麓区)六年级一班原有学生42人,其中男生占.后来转来女生若干人,这时男生与女生人数的比是6:5.现在全班有多少人?
【解答】解:42×=24(人)
24÷
=24÷
=44(人)
答:现在全班有44人.
比的意义(共1小题)
(2020 岳麓区)甲、乙、丙三个数,已知甲:(乙+丙)=4:3,乙:丙=2:7,求甲:乙:丙.
【解答】解:根据题意设乙为2a,丙为7a,则
可得乙+丙=2a+7a=9a
由甲:(乙+丙)=4:3得
甲=9a×4÷3=12a
所以甲:乙:丙=12a:2a:7a=12:2:7.
含字母式子的求值(共1小题)
(2020 岳麓区)已知==20092010,求.
【解答】解:设20092010为k,那么a=2k,b=3k,c=4k
当a=2k,b=3k,c=4k时
=
=
=.
14解答题
负数的意义及其应用(共1小题)
(2020 长沙)把几个数用大括号括起来,中间用逗号断开,如:{1,2,8}、{﹣2,7,,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数10﹣a也必是这个集合的元素,这样的集合我们称为“好的集合”.例如集合{10,0}就是一个“好的集合”.
(1)集合{﹣2,7,,19} (填“是”或“不是”)“好的集合”.
(2)请你再写出两个“好的集合”(不得与上面出现过的集合重复).
(3)在所有“好的集合”中,元素个数最少的集合是 .
“式”的规律(共1小题)
(2020 岳麓区)观察1+3=4;4+5=9;9+7=16;16+9=25;25+11=36这五道算式,找出规律,然后填写20012+ =20022.
简单周期现象中的规律(共1小题)
(2020 长沙)有同样大小的红、蓝、白玻璃球共76个,始终按2个红球、3个蓝球,4个白球的顺序排列.蓝玻璃球的个数占总数的.
圆与组合图形(共1小题)
(2020 长沙)图中是一个边长为4厘米的正方形,那么总的阴影面积是多少平方厘米?(π取3.14)
简单的立方体切拼问题(共1小题)
(2020 长沙)有n个同样大小的正方体,将它们摞成一个长方体,这个长方体的底面就是原正方体的底面.如果这个长方体的表面积是3096平方厘米,当从这个长方体的顶部拿去一个正方体后,新的长方体的表面积比原来长方体的表面积减少144平方厘米,那么n是多少?(写出简要解答步骤)
多边形的内角和(共1小题)
(2020 岳麓区)同学们都知道三角形内角和是180°,四边形内角和是360°,请你求出99边形的内角和。
组合图形的面积(共6小题)
(2022 长沙)如图,四边形ABCD是周长为80cm的正方形,在以C为圆心、CD为半径的扇形中,∠DCE=90°。求阴影部分的面积。(圆周率取3.14)
(2020 长沙)求如图直角梯形中阴影部分的面积.(单位:厘米)
(2020 岳麓区)如图,AF=2FB,FD=2EF,直角三角形ABC的面积是36平方厘米,求平行四边形EBCD的面积.
(2020 长沙)求面积。
(1)如图1在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是多少?
(2)求图2阴影部分的面积(π为3.14).
(2020 岳麓区)如图,△ABC的面积为14平方厘米,DC=3DB,AE=ED.求阴影部分的面积.
(2020 长沙)如图,甲、乙两个图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积.
(2021 长沙)一个圆和一个直角梯形按如图所示的方式重叠,求图中阴影部分的面积。(圆周率取3.14,单位:厘米)
(2020 雨花区)求阴影部分的周长.(大圆R=4.5,小圆r=2,单位:cm)
(2020 岳麓区)求图中阴影部分的面积(单位:分米)。
(2020 岳麓区)如图,两个正方形的边长分别是6厘米、4厘米,求阴影部分的面积。
重叠问题(共1小题)
(2020 长沙)两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米,如图那样重合,求重合部分(阴影部分)的面积。
圆、圆环的周长(共1小题)
(2020 长沙)求阴影部分的周长。(大圆R=4.5,小圆r=2,单位:cm)
三角形面积与底的正比关系(共2小题)
(2021 岳麓区)已知D是BC的中点,E是CD的中点,F是AC的中点.△ADG的面积比△EFG的面积大6平方厘米,△ABC的面积是多少?
(2020 长沙)如图,已知△ABC的面积为27,且BD=DC,AF=FD,CE=EF,求△DEF的面积。
圆柱的侧面积、表面积和体积(共1小题)
(2020 大同)一个底面周长是3.14分米的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的.将两个同样大小的鸡蛋放入杯子中,浸没在水中.这时水面上升8厘米,刚好与杯子口相平,求玻璃杯的容积.
因数与倍数(共1小题)
(2020 长沙)有3个吉利数:888,518,666,用它们分别除以同一个自然数,所得余数依次为a,a+7,a+10,求这个自然数.
体积的等积变形(共1小题)
(2020 长沙)如下面图1那样,在用塑料制的三棱柱形的筒里装着水,这个筒的展开图如下面图2.
现在,如图1那样,把这个筒的A面作为底面,放在水平的桌面上,水面高度是2cm.按上面讲的条件回答下列问题:
(1)把B面作为底面,放在水平的桌面上,水面高多少厘米?
(2)把C面(直角三角形的面)作为底面,放在水平的桌面上,水面高又是多少厘米?
逻辑推理(共1小题)
(2020 岳麓区)张凯靓、王全美、余鑫盈三位老师共同担任五(2)班的语文、数学、英语、音乐、美术和体育六门课的教学,每人教两门,现在知道:
(1)英语老师和数学老师是邻居;
(2)王全美年纪最小;
(3)张凯靓喜欢和体育老师、数学老师来往;
(4)体育老师比语文老师年龄大;
(5)王全美、语文老师、音乐老师三人经常一起做操。
请判断各人分别教的是哪两门课程.
列方程解含有两个未知数的应用(共2小题)
(2020 岳麓区)原来每个足球的价钱是每个篮球价钱的,每个足球和每个篮球的售价都提高3元后,每个足球的价钱是每个篮球价钱的,现在每个篮球售价 元.
(2020 岳麓区)一串数有11个数,中间一个数最大.从中间的数往前数,一个数比一个数小2;从中间的数往后数,一个数比一个数小3,这11个数的总和是200,那么中间的数是多少?
比的应用(共4小题)
(2021 长沙)有A、B两棵小树,现在高度均为80cm。A、B两棵树的生长速度之比为12:7。
(1)当A树长到104厘米高时,B树有多高?
(2)当A、B两树的高度之比为4:3时,A树高 厘米。(直接填出得数)
(2020 长沙)图书馆共进两批图书,第一批图书本数比第二批多10%,如果从第一批拿80本到第二批,这时第一批本数与第二批本数之比是3:4,图书馆这两批图书共进了多少本?
(2020 长沙)甲、乙两个班的学生人数的比是5:4,如果从乙班转走9名学生,那么甲班就比乙班人数多.这时乙班有多少人?
(2020 岳麓区)六年级一班原有学生42人,其中男生占.后来转来女生若干人,这时男生与女生人数的比是6:5.现在全班有多少人?
比的意义(共1小题)
(2020 岳麓区)甲、乙、丙三个数,已知甲:(乙+丙)=4:3,乙:丙=2:7,求甲:乙:丙.
含字母式子的求值(共1小题)
(2020 岳麓区)已知==20092010,求.
参考答案与试题解析
负数的意义及其应用(共1小题)
(2020 长沙)把几个数用大括号括起来,中间用逗号断开,如:{1,2,8}、{﹣2,7,,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数10﹣a也必是这个集合的元素,这样的集合我们称为“好的集合”.例如集合{10,0}就是一个“好的集合”.
(1)集合{﹣2,7,,19} 不是 (填“是”或“不是”)“好的集合”.
(2)请你再写出两个“好的集合”(不得与上面出现过的集合重复).
(3)在所有“好的集合”中,元素个数最少的集合是 {5} .
【解答】解:(1)集合{﹣2,7,,19}不是“好的集合”。
(2){3,7},{1,9}。
(3)在所有“好的集合”中,元素个数最少的集合是{5}。
故答案为:不是;{5}。
“式”的规律(共1小题)
(2020 岳麓区)观察1+3=4;4+5=9;9+7=16;16+9=25;25+11=36这五道算式,找出规律,然后填写20012+ 4003 =20022.
【解答】解:通过观察可以得出规律:相邻的两个自然数的平方差,得到的差等于这两个自然数的和.
20022﹣20012
=2002+2001
=4003
所以:20012+4003=20022.
故答案为:4003.
简单周期现象中的规律(共1小题)
(2020 长沙)有同样大小的红、蓝、白玻璃球共76个,始终按2个红球、3个蓝球,4个白球的顺序排列.蓝玻璃球的个数占总数的.
【解答】解:76÷9=8…4,
所以76个球共经历了8个周期零4个球,
所以蓝球的个数为:8×3+2=26(个),
26÷76=
答:蓝玻璃球的个数占总数的.
故答案为:.
圆与组合图形(共1小题)
(2020 长沙)图中是一个边长为4厘米的正方形,那么总的阴影面积是多少平方厘米?(π取3.14)
【解答】解:4÷2=2(厘米)
3.14×22÷2+4×4÷4
=6.28+4
=10.28(平方厘米)
答:总的阴影面积是10.28平方厘米。
简单的立方体切拼问题(共1小题)
(2020 长沙)有n个同样大小的正方体,将它们摞成一个长方体,这个长方体的底面就是原正方体的底面.如果这个长方体的表面积是3096平方厘米,当从这个长方体的顶部拿去一个正方体后,新的长方体的表面积比原来长方体的表面积减少144平方厘米,那么n是多少?(写出简要解答步骤)
【解答】解:正方体一个面的面积是:144÷4=36(平方厘米),根据长方体的表面积可得:
36×(4n+2)=3096,
144n+72=3096,
144n=3024,
n=21,
答:n是21.
多边形的内角和(共1小题)
(2020 岳麓区)同学们都知道三角形内角和是180°,四边形内角和是360°,请你求出99边形的内角和。
【解答】解:从四边形的一个顶点可以引出1条对角线,把四边形分成2个三角形,那么它的内角和是180°×2=360°,
从五边形的一个顶点可以引出2条对角线,把五边形分成3个三角形,那么它的内角和是180°×3=540°,
从六边形的一个顶点可以引出3条对角线,把六边形分成4个三角形,那么它的内角和是180°×4=720°,
…
从n(n大于或等于3)边形的一个顶点可以引出(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,那么n边形的内角和为180°×(n﹣2),
当n=99时,
180°×(99﹣2)
=180°×97
=17460°
答:99边形的内角和是17460°。
组合图形的面积(共6小题)
(2022 长沙)如图,四边形ABCD是周长为80cm的正方形,在以C为圆心、CD为半径的扇形中,∠DCE=90°。求阴影部分的面积。(圆周率取3.14)
【解答】解:正方形的边长为:80÷4=20(cm)
20×20÷2+3.14×202÷4
=400÷2+3.14×400÷4
=200+314
=514(平方厘米)
答:阴影部分的面积是514平方厘米。
(2020 长沙)求如图直角梯形中阴影部分的面积.(单位:厘米)
【解答】解:(3+4)×2÷2﹣3.14×22×﹣(4﹣2)×2÷2,
=7﹣3.14﹣2,
=1.86(平方厘米);
答:阴影部分的面积是1.86平方厘米.
(2020 岳麓区)如图,AF=2FB,FD=2EF,直角三角形ABC的面积是36平方厘米,求平行四边形EBCD的面积.
【解答】解:根据题意得出:
BC×3FB÷2=36
FB=36×2÷3÷BC
平行四边形EBCD的面积
BC×FB
=BC×(36×2÷3÷BC)
=36×2÷3
=24(平方厘米)
答:平行四边形EBCD的面积是24平方厘米.
(2020 长沙)求面积。
(1)如图1在直角梯形ABCD中,三角形ABE和三角形CDE都是等腰直角三角形,且BC=20厘米,那么直角梯形ABCD的面积是多少?
(2)求图2阴影部分的面积(π为3.14).
【解答】解:(1)20×20÷2=200(平方厘米)
答:梯形ABCD的面积是200平方厘米。
(2)×3.14×(8×6÷4.8÷2)2﹣8×6÷2
=×3.14×25﹣24
=39.25﹣24
=15.25
答:阴影部分的面积是15.25。
(2020 岳麓区)如图,△ABC的面积为14平方厘米,DC=3DB,AE=ED.求阴影部分的面积.
【解答】解:连接DF,
因为AE=DE,
所以S△AFE=S△DFE,S△ACE=S△DCE.
所以S△ACF=S△DCF.
又因为CD=3DB,
所以S△ACF=S△DCF=3S△BDF;
所以S△ABC=S△BDF×7=14,
故S△BDF=14÷7=2(平方厘米).
S阴影=S△DCF=S△BDF×3=2×3=6(平方厘米).
答:阴影部分的总面积是6平方厘米.
(2020 长沙)如图,甲、乙两个图形都是正方形,它们的边长分别是10厘米和12厘米,求阴影部分的面积.
【解答】解:12×12+10×10﹣(12+10)×12÷2﹣10×10÷2﹣(12﹣10)×12÷2
=144+100﹣132﹣50﹣12
=244﹣194
=50(平方厘米)
答:阴影部分的面积是50平方厘米.
53.(2021 长沙)一个圆和一个直角梯形按如图所示的方式重叠,求图中阴影部分的面积。(圆周率取3.14,单位:厘米)
【解答】解:(4+8)×4÷2﹣3.14×4×4×
=24﹣12.56
=11.44(平方厘米)
答:图中阴影部分的面积是11.44平方厘米。
54.(2020 雨花区)求阴影部分的周长.(大圆R=4.5,小圆r=2,单位:cm)
【解答】解:(4.5×2)×4+2×3.14×4.5+2×3.14×2
=9×4+28.26+12.56
=36+28.26+12.56
=76.82(厘米)
答:阴影部分的周长是76.82厘米。
55.(2020 岳麓区)求图中阴影部分的面积(单位:分米)。
【解答】解:如图:
7×4÷2+4×4÷2
=28÷2+16÷2
=14+8
=22(平方分米)
答:阴影部分的面积是22平方分米。
56.(2020 岳麓区)如图,两个正方形的边长分别是6厘米、4厘米,求阴影部分的面积。
【解答】解:如图分割:
S阴影=S三角形+S弓形
=×6×4+(×3.14×4×4﹣×4×4)
=3×4+(3.14×4﹣2×4)
=12+(12.56﹣8)
=12+12.56﹣8
=16.56(cm2)
答:阴影部分的面积为16.56平方厘米。
重叠问题(共1小题)
51.(2020 长沙)两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米,如图那样重合,求重合部分(阴影部分)的面积。
【解答】解:根据题干分析可得:
10×10÷2÷2﹣(10﹣6)×(10﹣6)÷2
=25﹣4×4÷2
=25﹣8
=17(平方厘米)
答:阴影部分的面积是17平方厘米。
圆、圆环的周长(共1小题)
52.(2020 长沙)求阴影部分的周长。(大圆R=4.5,小圆r=2,单位:cm)
【解答】解:4.5×2×4+2×3.14×4.5+2×3.14×2
=9×4+28.26+12.56
=36+28.26+12.56
=76.82(厘米)
答:阴影部分的周长是76.82厘米。
三角形面积与底的正比关系(共2小题)
58.(2021 岳麓区)已知D是BC的中点,E是CD的中点,F是AC的中点.△ADG的面积比△EFG的面积大6平方厘米,△ABC的面积是多少?
【解答】解:根据题干和图形可得:因为△ADG的面积﹣△EFG的面积=6平方厘米,
所以三角形ADE的面积﹣三角形FDE的面积=6平方厘米,
因为D是BC的中点,E是CD的中点,F是AC的中点,
所以三角形ADE的面积=三角形ADC的面积=三角形ABC的面积;
三角形FDE的面积=三角形FDC的面积=三角形ADC的面积=三角形ABC的面积,
所以三角形ABC的面积﹣三角形ABC的面积=6平方厘米,
即三角形ABC的面积=6平方厘米,
所以三角形ABC的面积为:6÷=48(平方厘米),
答:三角形ABC的面积是48平方厘米.
59.(2020 长沙)如图,已知△ABC的面积为27,且BD=DC,AF=FD,CE=EF,求△DEF的面积。
【解答】解:根据BD=DC,AF=FD,CE=EF,
可知,CD=BC,DF=AD,EF=CF;
△ABC与△ADC等高,底CD=BC,
所以,S△ACD=S△ABC×,
同理可得:S△CDF=S△ACD,S△DEF=S△CDF,
所以,S△DEF=××S△ABC
=×27
=8
答:△DEF的面积为8。
圆柱的侧面积、表面积和体积(共1小题)
(2020 大同)一个底面周长是3.14分米的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的.将两个同样大小的鸡蛋放入杯子中,浸没在水中.这时水面上升8厘米,刚好与杯子口相平,求玻璃杯的容积.
【解答】解:杯子高是:
8÷(1﹣)
=8
=8×3
=24(厘米);
3.14分米=31.4厘米,
3.14×(31.4÷3.14÷2)2×24
=3.14×52×24
=3.14×25×24
=1884(立方厘米);
答:玻璃杯子的容积是1884立方厘米.
因数与倍数(共1小题)
(2020 长沙)有3个吉利数:888,518,666,用它们分别除以同一个自然数,所得余数依次为a,a+7,a+10,求这个自然数.
【解答】解:518﹣7=511,666﹣10=656;888,511,656除以这个数,余数相同;888﹣511=377,888﹣656=232,这个数为377与232的公因数,且大于10,
因为377=13×29,232=8×29,所以这个自然数为29;
答:这个自然数是29.
体积的等积变形(共1小题)
(2020 长沙)如下面图1那样,在用塑料制的三棱柱形的筒里装着水,这个筒的展开图如下面图2.
现在,如图1那样,把这个筒的A面作为底面,放在水平的桌面上,水面高度是2cm.按上面讲的条件回答下列问题:
(1)把B面作为底面,放在水平的桌面上,水面高多少厘米?
(2)把C面(直角三角形的面)作为底面,放在水平的桌面上,水面高又是多少厘米?
【解答】解:在图中标上字母如下图所示,
因X是MN的中点,故Y也是MP的中点,△MXY,△MNP都是直角三角形;
利用勾股定理,可求出XY=1.5cm,水的体积为:
(1.5+3)×2÷2×12=54(cm3);
当YZ与PN垂直,交NP于Z时,XY=NZ=ZP=1.5cm,XN=YZ=2cm;
故三角形XYM与三角形YZP完全一样.
(1)当B作底面时,侧面PMN如下图所示,
因为△YZM与△XYP完全一样.故水深1.5cm.
(2)因高=体积÷底面积,
所以△NMP面积:3×4÷2=6(cm2);
高为:54÷6=9(cm).
答:把B面作为底面,水面高1.5厘米;把C面作为底面,水面高是9厘米.
逻辑推理(共1小题)
(2020 岳麓区)张凯靓、王全美、余鑫盈三位老师共同担任五(2)班的语文、数学、英语、音乐、美术和体育六门课的教学,每人教两门,现在知道:
(1)英语老师和数学老师是邻居;
(2)王全美年纪最小;
(3)张凯靓喜欢和体育老师、数学老师来往;
(4)体育老师比语文老师年龄大;
(5)王全美、语文老师、音乐老师三人经常一起做操。
请判断各人分别教的是哪两门课程.
【解答】解:根据题意知:
(1)英语老师和数学老师不是一个人;
(2)王全美老师最年轻;
(3)张凯靓老师不是体育老师,也不是数学老师,而且体育老师和数学老师不是一个人;
(4)王全美不是体育老师;
(5)王全美老师不是语文老师,也不是音乐老师,而且音乐老师和语文老师是两个人。
综合条件(3)(4)可知,体育老师是余鑫盈老师,数学老师是王全美老师。由条件(5)可知,王全美老师不是音乐老师和语文老师,语文老师是张凯靓老师;所以音乐老师是谁时不能确定;由于英语老师和数学老师是邻居,所以英语老师不是王全美老师,而王全美老师只能是美术老师;由于王全美老师与音乐老师和语文老师经常一起做操,所以张凯靓老师教语文不教音乐,所以音乐老师是余鑫盈老师;张凯靓老师是英语老师。
答:张凯靓老师教语文和英语;王全美老师教数学和美术;余鑫盈老师教体育和音乐。
列方程解含有两个未知数的应用(共2小题)
(2020 岳麓区)原来每个足球的价钱是每个篮球价钱的,每个足球和每个篮球的售价都提高3元后,每个足球的价钱是每个篮球价钱的,现在每个篮球售价 57 元.
【解答】解:设原来每个篮球的价钱是x元,则原来每个足球的价钱是x元,
x+3=(x+3)×
x+3=x+
x+3﹣x=x+﹣x
x+=3
x+﹣=3﹣
x=
x÷=÷
x=54
54+3=57(元)
答:现在每个篮球售价57元.
故答案为:57.
(2020 岳麓区)一串数有11个数,中间一个数最大.从中间的数往前数,一个数比一个数小2;从中间的数往后数,一个数比一个数小3,这11个数的总和是200,那么中间的数是多少?
【解答】解:设中间的数是x,则这11个数依次是:x﹣10,x﹣8,x﹣6,x﹣4,x﹣2,x,x﹣3,x﹣6,x﹣9,x﹣12,x﹣15,可得方程:
11x﹣(2+4+6+8+10)﹣(3+6+9+12+15)=200,
11x=200+30+45,
x=25.
答:中间的数是25.
比的应用(共4小题)
(2021 长沙)有A、B两棵小树,现在高度均为80cm。A、B两棵树的生长速度之比为12:7。
(1)当A树长到104厘米高时,B树有多高?
(2)当A、B两树的高度之比为4:3时,A树高 200 厘米。(直接填出得数)
【解答】解:(1)(104﹣80)×+80
=24×+80
=14+80
=94(厘米)
答:B树有94厘米高。
(2)设A树长12x厘米,则B树长7x厘米。
(80+12x):(80+7x)=4:3
3(80+12x)=4(80+7x)
240+36x=320+28x
36x﹣28x=320﹣240
8x=80
x=10
80+12×10
=80+120
=200(厘米)
答:A树高200厘米。
故答案为:200。
(2020 长沙)图书馆共进两批图书,第一批图书本数比第二批多10%,如果从第一批拿80本到第二批,这时第一批本数与第二批本数之比是3:4,图书馆这两批图书共进了多少本?
【解答】解:设第二批进了x本,则第一批进了(1+10%)x本,根据从第一批拿80本到第二批.由题意
=
=
(1.1x﹣80)×4=(x+80)×3
4.4x﹣320=3x+240
4.4x﹣320+320﹣3x=3x+240+320﹣3x
1.4x=560
1.4x÷1.4=560÷1.4
x=400
400×(1+10)+400
=400×1.1+400
=440+400
=840(本)
答:图书馆这两批图书共进了840本.
(2020 长沙)甲、乙两个班的学生人数的比是5:4,如果从乙班转走9名学生,那么甲班就比乙班人数多.这时乙班有多少人?
【解答】解:甲班比乙班多,
此时乙班学生占3份,甲班学生就是这样的3+2=5(份)
由于甲班份数刚好没有变,所以乙班转走的9名同学刚好是4﹣3=1(份)
所以这时乙班人数是:9×3=27(人)
答:这时乙班有27人.
(2020 岳麓区)六年级一班原有学生42人,其中男生占.后来转来女生若干人,这时男生与女生人数的比是6:5.现在全班有多少人?
【解答】解:42×=24(人)
24÷
=24÷
=44(人)
答:现在全班有44人.
比的意义(共1小题)
(2020 岳麓区)甲、乙、丙三个数,已知甲:(乙+丙)=4:3,乙:丙=2:7,求甲:乙:丙.
【解答】解:根据题意设乙为2a,丙为7a,则
可得乙+丙=2a+7a=9a
由甲:(乙+丙)=4:3得
甲=9a×4÷3=12a
所以甲:乙:丙=12a:2a:7a=12:2:7.
含字母式子的求值(共1小题)
(2020 岳麓区)已知==20092010,求.
【解答】解:设20092010为k,那么a=2k,b=3k,c=4k
当a=2k,b=3k,c=4k时
=
=
=.
同课章节目录
