13.3.1 等腰三角形的性质 课件(共27张PPT)
文档属性
| 名称 | 13.3.1 等腰三角形的性质 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-06 09:40:07 | ||
图片预览





文档简介
(共27张PPT)
13.3.1等腰三角形的性质
人教版八年级上册
知识回顾
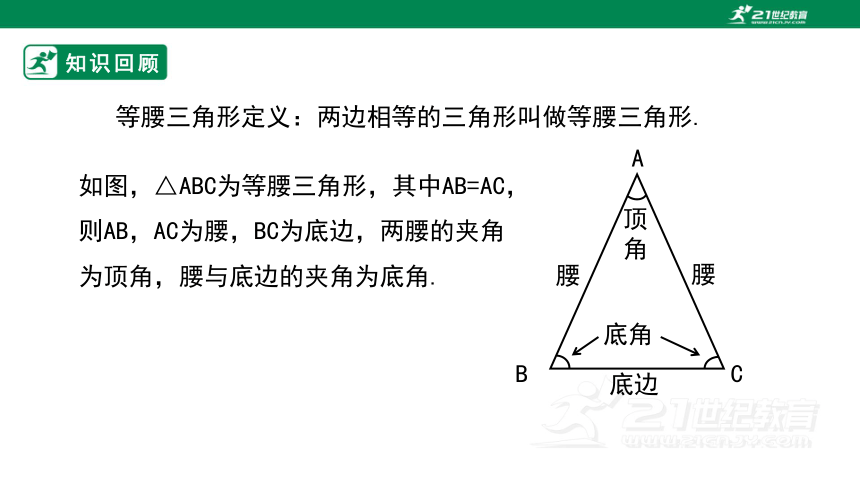
等腰三角形定义:两边相等的三角形叫做等腰三角形.
如图,△ABC为等腰三角形,其中AB=AC,则AB,AC为腰,BC为底边,两腰的夹角为顶角,腰与底边的夹角为底角.
A
B
C
腰
腰
底边
顶
角
底角
教学目标
1.了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.
2.探索、掌握等腰三角形的性质,并能解决相关实际问题.
新知导入
新知探究
等腰三角形的性质
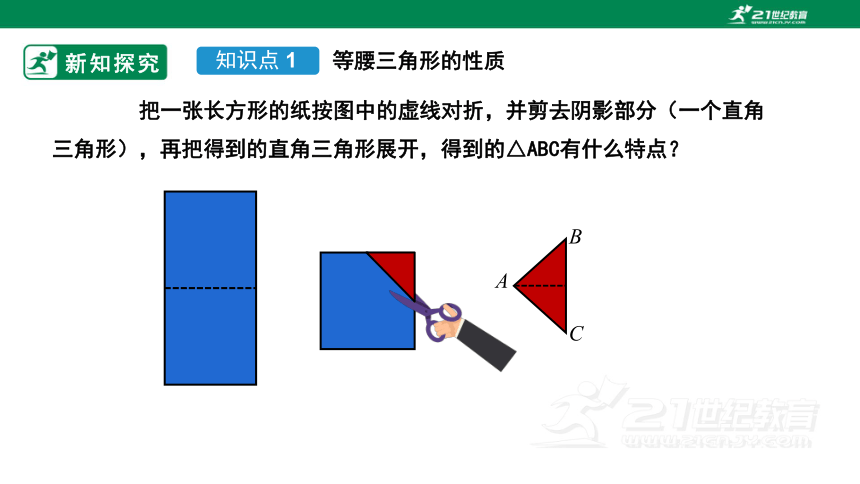
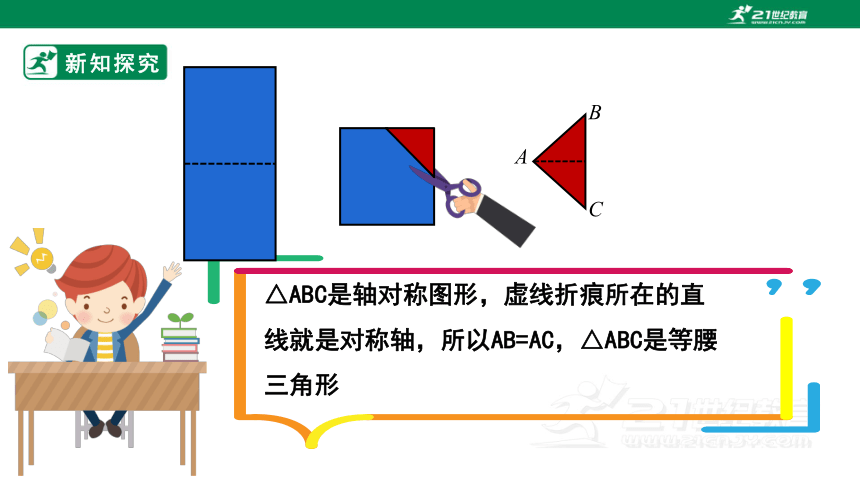
把一张长方形的纸按图中的虚线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的△ABC有什么特点?
知识点 1
A
B
C
新知探究
△ABC是轴对称图形,虚线折痕所在的直线就是对称轴,所以AB=AC,△ABC是等腰三角形
A
B
C
新知探究
剪出的等腰三角形是轴对称图形吗?把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.
A
C
B
D
重合的线段 重合的角
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜想1:等腰三角形的底角相等。
猜想2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
新知探究
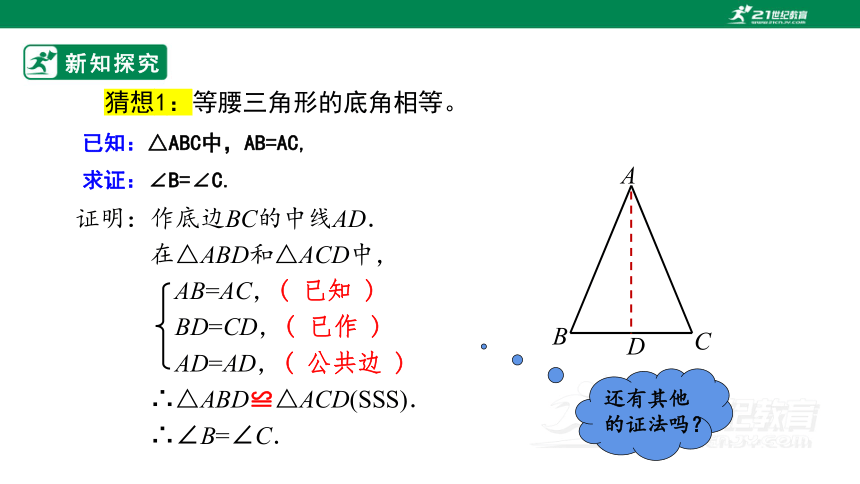
猜想1:等腰三角形的底角相等。
已知:△ABC中,AB=AC,
求证:∠B=∠C.
A
B
C
D
证明:作底边BC的中线AD.
在△ABD和△ACD中,
AB=AC,( 已知 )
BD=CD,( 已作 )
AD=AD,( 公共边 )
∴△ABD≌△ACD(SSS).
∴∠B=∠C.
还有其他的证法吗?
新知探究
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
探究新知
证明:作底边BC的高AD,交BC于点D.
∵AD⊥BC,
∴ ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
∴ Rt△ABD ≌ Rt△ACD(HL),
∴ ∠B=∠C.
A
B
C
D
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
方法三:作底边上的高
课堂小结
等腰三角形性质1:等腰三角形的两个底角相等
(简称:等边对等角).
A
C
B
几何语言:
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
应用“等边对等角”的前提条件是在同一个三角形中.
新知典例
方法点拨:在含多个等腰三角形的图形中求角时,常常利用方程思想,通过内角、外角之间的关系进行转化求解.
例1 如图,在等腰△ABC中,AB=AC,延长BC到点D,使得CD=CA,连接AD,若∠D=25°,求∠BAC的度数.
解:∵CD=CA,∠D=25°,
∴∠CAD=25°
∴∠BCA=2∠D=50°,
∵AB=AC,
∴∠B=∠BCA=50°,
∴∠BAC=180°﹣∠B﹣∠C=80°.
课堂练习
1. 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
∴∠A=36°,∠ABC=∠C=72°.
证明:∵AD平分∠BAC,∴∠BAD=∠CAD.
AB=AC,
在△ABD和△ACD中,∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS),
∴∠ADB=∠ADC,BD=CD即AD为BC的中线.
∵ ∠ADB+∠ADC=180°,∴AD⊥BC.
探究新知
猜想2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
如图,在△ABC中,AB=AC ,AD平分∠BAC,
求证:AD⊥BC,BD=CD .
B
C
D
A
证明:∵AD是底边BC的中线,∴BD=CD.
AB=AC,
在△ABD和△ACD中, BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠ADB=∠ADC,∠BAD=∠CAD即
AD为∠CAB的平分线.
∵ ∠ADB+∠ADC=180°,∴AD⊥BC.
探究新知
如图,在△ABC中,AB=AC,AD是底边BC的中线,
求证:AD⊥BC,AD平分∠BAC.
A
B
C
D
新知探究
如图,在△ABC中,AB=AC, AD是底边BC的高,
求证: AD平分∠BAC ,BD=CD.
B
C
D
A
证明:∵AD是底边BC的高,∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,AB=AC,
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
∴BD=CD,∠BAD=∠CAD .
课堂小结
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
即:等腰三角形
顶角平分线
底边上的高线
底边上的中线
具备其
中一条
另外两条成立
课堂小结
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
几何语言:如图, 在△ABC中,
A
B
C
D
(
(
1
2
(1)∵AB=AC, AD⊥BC,
∴∠_____ = ∠_____,____= ____.
1
2
BD
CD
(2) ∵AB=AC, AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3) ∵AB=AC, AD是角平分线,
∴____ ⊥____ ,_____ =_____.
2
AD
BC
BD
1
BC
AD
CD
新知典例
例2 如图 ,已知点D、E在△ABC的边BC上,AB=AC.
若BD=CE,F为DE的中点.
求证:AF⊥BC.
证明:∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
方法点拨:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线
课堂小练
2.如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
证明:如图,过点A作AP⊥BC于P.
∵AB=AC,
∴BP=PC;
∵AD=AE,
∴DP=PE,
∴BP﹣DP=PC﹣PE,
∴BD=CE.
P
课堂小测
1.如图,已知在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点D,交AB于点E,连接BD,则∠DBC的度数为( )
A.30° B.32°
C.34° D.36°
A
2.如图,在△ABC中,AB=AC,以点B为圆心,BC的长为半径画弧交AC于点C、E,再分别以点C与点E为圆心,大于CE长的一半为半径画弧,两弧交于点F,连接BF交AC于点D,若∠A=50°,则∠CBD的大小是( )
A.25° B.40° C.50° D.65°
A
当堂小测
3.如图,已知∠A=13°,AB=BC=CD,那么∠BCD= 度.
128
4.如图,△ABC中,AB=AC,∠ABC=40°,点D在线段BC上运动(点D不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.当△ADE是等腰三角形时,∠BAD的度数为 .
60°或30°
当堂小测
5.如图,在△ABC中,AB=AC,∠B+∠C=60°,BC=15cm,ED、FG分别是AB、AC的垂直平分线,求GE的长.
解:连接AE,AG,
∵∠B+∠C=60°,AB=AC,
∴∠B=∠C=30°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠DAE=∠B=30°.
∵GF是AC的垂直平分线,
∴AG=CG,
∴∠CAG=∠C=30°.
∴∠AEG=60°,∠AGE=60°,
∴△EAG是等边三角形,
∴AE=AG=EG,
∵BC=15cm,
∴GE=5cm.
课堂总结
等腰
三角形
定义
性质
有两边相等的三角形
等边对等角
三线合一
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
13.3.1等腰三角形的性质
人教版八年级上册
知识回顾
等腰三角形定义:两边相等的三角形叫做等腰三角形.
如图,△ABC为等腰三角形,其中AB=AC,则AB,AC为腰,BC为底边,两腰的夹角为顶角,腰与底边的夹角为底角.
A
B
C
腰
腰
底边
顶
角
底角
教学目标
1.了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.
2.探索、掌握等腰三角形的性质,并能解决相关实际问题.
新知导入
新知探究
等腰三角形的性质
把一张长方形的纸按图中的虚线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的△ABC有什么特点?
知识点 1
A
B
C
新知探究
△ABC是轴对称图形,虚线折痕所在的直线就是对称轴,所以AB=AC,△ABC是等腰三角形
A
B
C
新知探究
剪出的等腰三角形是轴对称图形吗?把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.
A
C
B
D
重合的线段 重合的角
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜想1:等腰三角形的底角相等。
猜想2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
新知探究
猜想1:等腰三角形的底角相等。
已知:△ABC中,AB=AC,
求证:∠B=∠C.
A
B
C
D
证明:作底边BC的中线AD.
在△ABD和△ACD中,
AB=AC,( 已知 )
BD=CD,( 已作 )
AD=AD,( 公共边 )
∴△ABD≌△ACD(SSS).
∴∠B=∠C.
还有其他的证法吗?
新知探究
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
探究新知
证明:作底边BC的高AD,交BC于点D.
∵AD⊥BC,
∴ ∠ADB =∠ADC=90°.
在Rt△ABD与Rt△ACD中,
AB=AC(已知),
AD=AD(公共边),
∴ Rt△ABD ≌ Rt△ACD(HL),
∴ ∠B=∠C.
A
B
C
D
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
方法三:作底边上的高
课堂小结
等腰三角形性质1:等腰三角形的两个底角相等
(简称:等边对等角).
A
C
B
几何语言:
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
应用“等边对等角”的前提条件是在同一个三角形中.
新知典例
方法点拨:在含多个等腰三角形的图形中求角时,常常利用方程思想,通过内角、外角之间的关系进行转化求解.
例1 如图,在等腰△ABC中,AB=AC,延长BC到点D,使得CD=CA,连接AD,若∠D=25°,求∠BAC的度数.
解:∵CD=CA,∠D=25°,
∴∠CAD=25°
∴∠BCA=2∠D=50°,
∵AB=AC,
∴∠B=∠BCA=50°,
∴∠BAC=180°﹣∠B﹣∠C=80°.
课堂练习
1. 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 ° ,
解得x=36 ° .
∴∠A=36°,∠ABC=∠C=72°.
证明:∵AD平分∠BAC,∴∠BAD=∠CAD.
AB=AC,
在△ABD和△ACD中,∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS),
∴∠ADB=∠ADC,BD=CD即AD为BC的中线.
∵ ∠ADB+∠ADC=180°,∴AD⊥BC.
探究新知
猜想2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
如图,在△ABC中,AB=AC ,AD平分∠BAC,
求证:AD⊥BC,BD=CD .
B
C
D
A
证明:∵AD是底边BC的中线,∴BD=CD.
AB=AC,
在△ABD和△ACD中, BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠ADB=∠ADC,∠BAD=∠CAD即
AD为∠CAB的平分线.
∵ ∠ADB+∠ADC=180°,∴AD⊥BC.
探究新知
如图,在△ABC中,AB=AC,AD是底边BC的中线,
求证:AD⊥BC,AD平分∠BAC.
A
B
C
D
新知探究
如图,在△ABC中,AB=AC, AD是底边BC的高,
求证: AD平分∠BAC ,BD=CD.
B
C
D
A
证明:∵AD是底边BC的高,∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,AB=AC,
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
∴BD=CD,∠BAD=∠CAD .
课堂小结
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
即:等腰三角形
顶角平分线
底边上的高线
底边上的中线
具备其
中一条
另外两条成立
课堂小结
性质2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
几何语言:如图, 在△ABC中,
A
B
C
D
(
(
1
2
(1)∵AB=AC, AD⊥BC,
∴∠_____ = ∠_____,____= ____.
1
2
BD
CD
(2) ∵AB=AC, AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3) ∵AB=AC, AD是角平分线,
∴____ ⊥____ ,_____ =_____.
2
AD
BC
BD
1
BC
AD
CD
新知典例
例2 如图 ,已知点D、E在△ABC的边BC上,AB=AC.
若BD=CE,F为DE的中点.
求证:AF⊥BC.
证明:∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
方法点拨:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线
课堂小练
2.如图,点D、E在△ABC的BC边上,AB=AC,AD=AE.求证:BD=CE.
证明:如图,过点A作AP⊥BC于P.
∵AB=AC,
∴BP=PC;
∵AD=AE,
∴DP=PE,
∴BP﹣DP=PC﹣PE,
∴BD=CE.
P
课堂小测
1.如图,已知在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AC于点D,交AB于点E,连接BD,则∠DBC的度数为( )
A.30° B.32°
C.34° D.36°
A
2.如图,在△ABC中,AB=AC,以点B为圆心,BC的长为半径画弧交AC于点C、E,再分别以点C与点E为圆心,大于CE长的一半为半径画弧,两弧交于点F,连接BF交AC于点D,若∠A=50°,则∠CBD的大小是( )
A.25° B.40° C.50° D.65°
A
当堂小测
3.如图,已知∠A=13°,AB=BC=CD,那么∠BCD= 度.
128
4.如图,△ABC中,AB=AC,∠ABC=40°,点D在线段BC上运动(点D不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.当△ADE是等腰三角形时,∠BAD的度数为 .
60°或30°
当堂小测
5.如图,在△ABC中,AB=AC,∠B+∠C=60°,BC=15cm,ED、FG分别是AB、AC的垂直平分线,求GE的长.
解:连接AE,AG,
∵∠B+∠C=60°,AB=AC,
∴∠B=∠C=30°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠DAE=∠B=30°.
∵GF是AC的垂直平分线,
∴AG=CG,
∴∠CAG=∠C=30°.
∴∠AEG=60°,∠AGE=60°,
∴△EAG是等边三角形,
∴AE=AG=EG,
∵BC=15cm,
∴GE=5cm.
课堂总结
等腰
三角形
定义
性质
有两边相等的三角形
等边对等角
三线合一
作业布置
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
