华师大版八年级数学上册 第13章 全等三角形 单元测试卷(word版含答案)
文档属性
| 名称 | 华师大版八年级数学上册 第13章 全等三角形 单元测试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 685.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-11 10:52:28 | ||
图片预览



文档简介
华师大版八年级数学上册单元测试卷
第13章 全 等 三 角 形
时间:60分钟 总分:120分
一、选择题 (每题3分,共24分)
1.在等腰△ABC中有一个角是50°,那么另外两个角分别是 ( )
A.50°、80° B.50°、80°或 65°、65°
C.65°、65° D.无法确定
2.对假命题“若a>b,则a2>b2”举一个反例,符合要求的反例是( )
A.a=﹣1,b=﹣2 B.a=2,b=一1
C.a=2,b=1 D.a=﹣1,b=0
3.下列命题中,是假命题的是 ( )
A.对顶角相等
B.同旁内角互补
C.全等三角形的对应边相等
D.角平分线上的点到这个角的两边的距离相等
4.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,△ABC的周长为 ( )
A.16 B.13 C.19 D.10
5.用直尺和圆规作一个角的角平分线的示意图如图所示,其中说明△COE≌△DOE的依据是 ( )
A.SSS B.SAS C.ASA D.AAS
6.如图,在△ABC中,边AB,AC的垂直平分线交于点P,连接BP,CP,若∠A=50°,∠PBC= ( )
A.40° B.50° C.80° D.100°
7.如图,在△ABC中,以A为圆心,适当长为半径作弧,分别交AB、AC于点D、E,再分别以D、E为圆心,相同长为半径作弧,分别交DB、EC于点F、G,连接EF、DG,交于点H,连接AH并延长交BC于点I,则线段AI是( )
A.△ABC的高 B.△ABC的中线
C.△ABC的角平分线 D.以上都不对
8.如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为 ( )
A.54° B.50° C.48° D.46°
二.填空题(每题3分,共24分)
9.已知△ABC的三边长为x,3,6,△DEF的三边长为5,6,y.若△ABC与△DEF全等,则x+y的值为 .
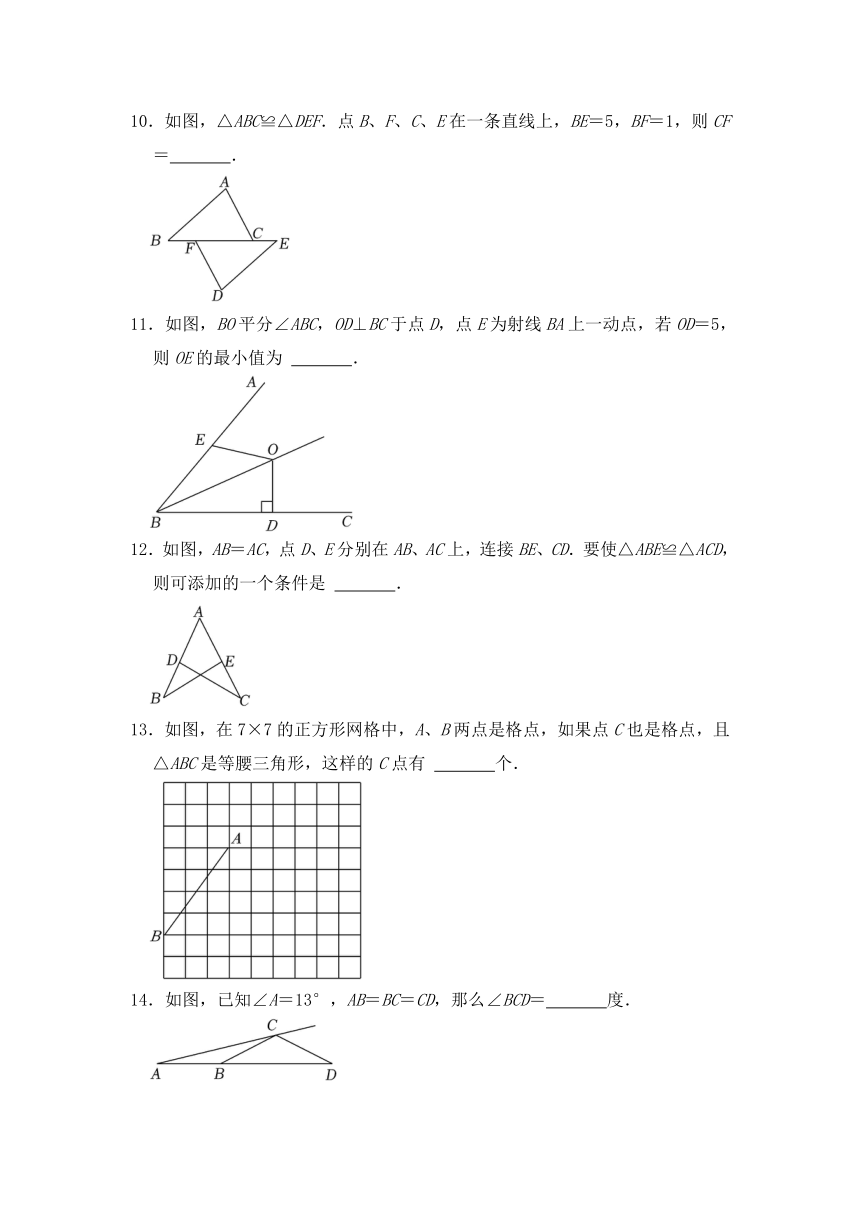
10.如图,△ABC≌△DEF.点B、F、C、E在一条直线上,BE=5,BF=1,则CF= .
11.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=5,则OE的最小值为 .
12.如图,AB=AC,点D、E分别在AB、AC上,连接BE、CD.要使△ABE≌△ACD,则可添加的一个条件是 .
13.如图,在7×7的正方形网格中,A、B两点是格点,如果点C也是格点,且△ABC是等腰三角形,这样的C点有 个.
14.如图,已知∠A=13°,AB=BC=CD,那么∠BCD= 度.
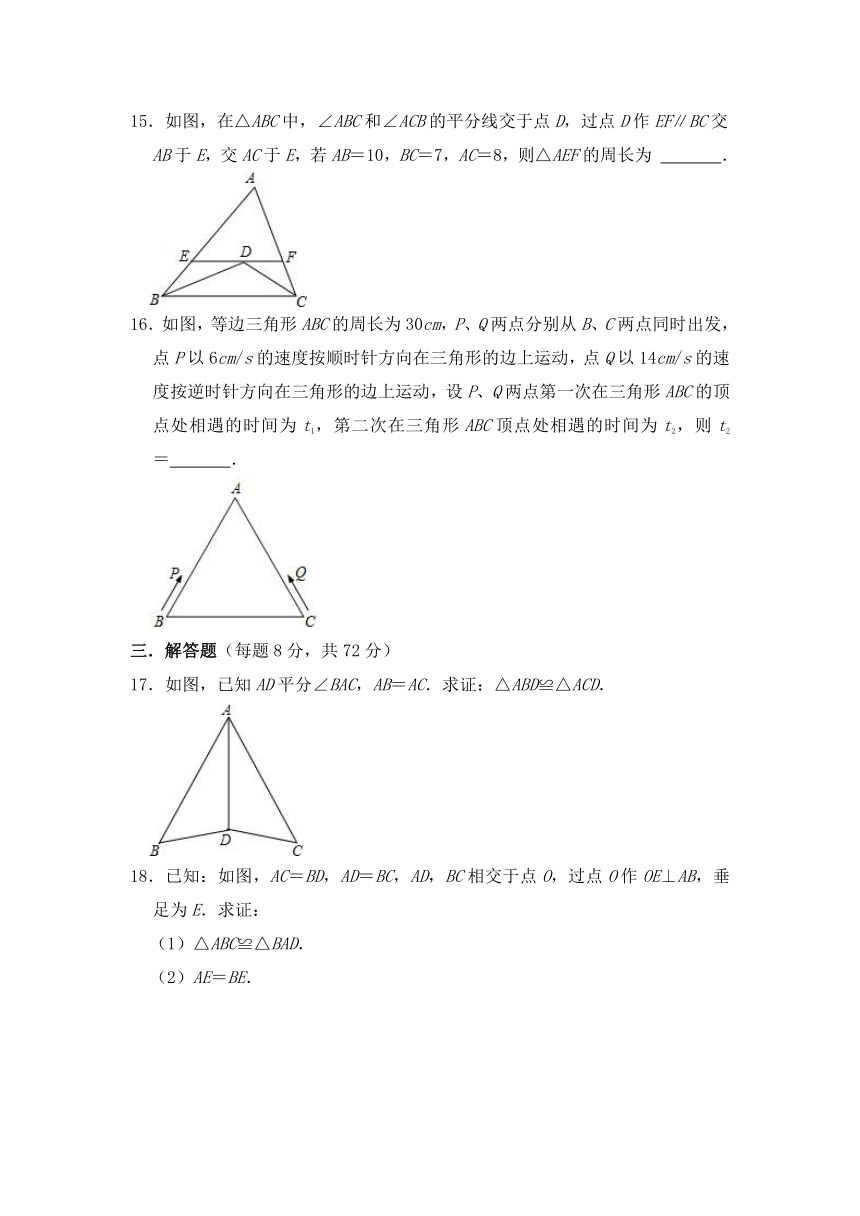
15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于E,若AB=10,BC=7,AC=8,则△AEF的周长为 .
16.如图,等边三角形ABC的周长为30cm,P、Q两点分别从B、C两点同时出发,点P以6cm/s的速度按顺时针方向在三角形的边上运动,点Q以14cm/s的速度按逆时针方向在三角形的边上运动,设P、Q两点第一次在三角形ABC的顶点处相遇的时间为t1,第二次在三角形ABC顶点处相遇的时间为t2,则t2= .
三.解答题(每题8分,共72分)
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
18.已知:如图,AC=BD,AD=BC,AD,BC相交于点O,过点O作OE⊥AB,垂足为E.求证:
(1)△ABC≌△BAD.
(2)AE=BE.
19.在等边△ABC中,点D,E分别在边BC,AB上,且BE=CD,AD与CE交于点F.求证:△AEC≌△BDA.
20.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=60°时,求∠EDF的度数.
21.新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.求证:BD=CE.
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,点D、E均在△ABC外,连接BD、CE交于点M,连接AM,求证:AM平分∠BME.
22.在△ABC中,AB=AC,D是BC边的中点,E、F分别是AD、AC边上的点.
(1)如图①,连接BE、EF,若∠ABE=∠EFC,求证:BE=EF;
(2)如图②,若B、E、F在一条直线上,且∠ABE=∠BAC=45°,探究BD与AE的数量之间有何等量关系,并说明理由.
23.如图,△ABC中,BD平分∠ABC,交AC于点D,AE⊥BD,垂足为点F.
(1)求证:AD=DE;
(2)若∠ABC=∠C=45°,求证:AD=EC.
24.如图,在△ACB中,AD为△ACB的角平分线,E为射线CB上的一点,过E点作EF⊥AB,垂足为F.
(1)若∠ACB=90°,当点E在线段CD上时,EF交AD于G点.
①如图1,求证:∠EGD=∠EDG.
②画∠CEF的角平分线分别交AC和BA的延长线于M,N点.请在图1中补全图形,并求证:∠MNA=∠CAD.
(2)如图2,若点E在CB延长线上,EP平分∠CEF交AD延长线于点P,试判断∠C与∠P的数量关系,并说明理由.
25.综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
参考答案与试题解析
一.选择题(每题3分,共24分)
1.在等腰△ABC中有一个角是50°,那么另外两个角分别是( )
A.50°、80° B.50°、80°或 65°、65°
C.65°、65° D.无法确定
解:当∠B=50°为顶角时,
此时∠A=∠C==65°;
当∠B=50°为底角时,
此时另一底角为50°,顶角为80°,
故另外两个角分别是50°,80°或65°,65°.
故选:B.
2.对假命题“若a>b,则a2>b2”举一个反例,符合要求的反例是( )
A.a=﹣1,b=﹣2 B.a=2,b=一1 C.a=2,b=1 D.a=﹣1,b=0
解:当a=﹣1,b=﹣2时,a>b,而a2<b2,
∴“若a>b,则a2>b2”是假命题,
故选:A.
3.下列命题中,是假命题的是( )
A.对顶角相等
B.同旁内角互补
C.全等三角形的对应边相等
D.角平分线上的点到这个角的两边的距离相等
解:A、对顶角相等,本选项说法是真命题,不符合题意;
B、两直线平行,同旁内角互补,故本选项说法是假命题,符合题意;
C、全等三角形的对应边相等,本选项说法是真命题,不符合题意;
D、角平分线上的点到这个角的两边的距离相等,本选项说法是真命题,不符合题意;
故选:B.
4.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,△ABC的周长为( )
A.16 B.13 C.19 D.10
解:∵DE是AC的垂直平分线,AE=3,
∴DA=DC,AC=2AE=6,
∵△ABD的周长为13,
∴AB+BD+AD=AB+BD+DC=AB+BC=13,
∴△ABC的周长=AB+BC+AC=13+6=19,
故选:C.
5.用直尺和圆规作一个角的角平分线的示意图如图所示,其中说明△COE≌△DOE的依据是( )
A.SSS B.SAS C.ASA D.AAS
解:根据作图的过程可知:
OC=OD,CE=DE,OE=OE
∴△OCE≌△ODE(SSS)
∴∠COE=∠DOE
故选:A.
6.如图,在△ABC中,边AB,AC的垂直平分线交于点P,连接BP,CP,若∠A=50°,∠PBC=( )
A.40° B.50° C.80° D.100°
解:连接AP,
在△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵边AB,AC的垂直平分线交于点P,
∴PA=PB,PA=PC,
∴∠PAB=∠PBA,∠PAC=∠PCA,PB=PC,
∴∠PBA+∠PCA=∠PAB+∠PAC=50°,
∴∠PBC+∠PCB=130°﹣50°=80°,
∵PB=PC,
∴∠PBC=∠PCB=40°,
故选:A.
7.如图,在△ABC中,以A为圆心,适当长为半径作弧,分别交AB、AC于点D、E,再分别以D、E为圆心,相同长为半径作弧,分别交DB、EC于点F、G,连接EF、DG,交于点H,连接AH并延长交BC于点I,则线段AI是( )
A.△ABC的高 B.△ABC的中线
C.△ABC的角平分线 D.以上都不对
解:由作图可知,AE=AD,AG=AF,
在△AFE和△AGD中,
,
∴△AFE≌△AGD(SAS),
∴∠AFE=∠AGD,
∵AG=AF,AE=AD,
∴EG=DF,
在△EHG和△DHF中,
,
∴△EHG≌△DHF(AAS),
∴EH=DH,
在△AHE和△AHD中,
,
∴△AHE≌△AHD(SSS),
∴∠EAH=∠DAH,
∴AI是△ABC的角平分线.
故选:C.
8.如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
解:如图所示,过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DF=DE,
又∵∠ACD=136°,∠BCD=44°,
∴∠ACB=92°,∠DCF=44°,
∴CD平分∠BCF,
又∵DF⊥AC于F,DG⊥BC于G,
∴DF=DG,
∴DE=DG,
∴BD平分∠CBE,
∴∠DBE=∠CBE,
∵AD平分∠BAC,
∴∠BAD=∠BAC,
∴∠ADB=∠DBE﹣∠BAD=(∠CBE﹣∠BAC)=∠ACB=×92°=46°,
故选:D.
二.填空题(每题3分,共24分)
9.已知△ABC的三边长为x,3,6,△DEF的三边长为5,6,y.若△ABC与△DEF全等,则x+y的值为 8 .
解:因为△ABC与△DEF全等,
所以x=5,y=3,
所以x+y=8,
故答案为:8.
10.如图,△ABC≌△DEF.点B、F、C、E在一条直线上,BE=5,BF=1,则CF= 3 .
解:∵△ABC≌△DEF,
∴BC=EF,
∴BF=EC=1,
∴FC=BE﹣BF﹣EC=5﹣1﹣1=3.
故答案为:3.
11.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=5,则OE的最小值为 5 .
解:∵BO平分∠ABC,OD⊥BC于点D,OD=5,
∴O到AB的距离等于OD的长,
根据垂线段最短,可知OE最小值为5.
故答案为:5.
12.如图,AB=AC,点D、E分别在AB、AC上,连接BE、CD.要使△ABE≌△ACD,则可添加的一个条件是 ∠B=∠C .
解:在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA).
故答案为:∠B=∠C.(答案不唯一).
13.如图,在7×7的正方形网格中,A、B两点是格点,如果点C也是格点,且△ABC是等腰三角形,这样的C点有 8 个.
解:以A为圆心,AB的长为半径作圆,此时C点有4个,
以B为圆心,AB的长为半径作圆,此时C点有4个,
作AB的垂直平分线,此时C点有0个,
故答案为:8.
14.如图,已知∠A=13°,AB=BC=CD,那么∠BCD= 128 度.
解:∵AB=BC,
∴∠BCA=∠A=13°,
∴∠CBD=∠A+∠BCD=26°,
又∵BC=CD,
∴∠CBD=∠D=26°,
∴∠BCD=180°﹣∠CBD﹣∠D=128°.
故答案为:128.
15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于E,若AB=10,BC=7,AC=8,则△AEF的周长为 18 .
解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵BD平分∠ABC,CD平分∠ACB,
∴∠ABD=∠DBC,∠ACD=∠DCB,
∴∠ABD=∠EDB,∠ACD=∠FDC,
∴EB=ED,FD=FC,
∴△AEF的周长=AE+EF+AF
=AE+ED+DF+AF
=AE+BE+CF+AF
=AB+AC
=10+8
=18,
故答案为:18.
16.如图,等边三角形ABC的周长为30cm,P、Q两点分别从B、C两点同时出发,点P以6cm/s的速度按顺时针方向在三角形的边上运动,点Q以14cm/s的速度按逆时针方向在三角形的边上运动,设P、Q两点第一次在三角形ABC的顶点处相遇的时间为t1,第二次在三角形ABC顶点处相遇的时间为t2,则t2= 25s .
解:∵等边三角形ABC的周长为30cm,
∴△ABC的边长为10cm,
由题意知,P、Q第一次时间为20÷(6+14)=1(秒)
以后每隔30÷(6+14)=1.5秒,P、Q就会相遇一次,
设P、Q相遇次数为n次,则
当6×1+6×1.5(n﹣1)=10k(k为正整数)时,P、Q两点就在三角形ABC的顶点处相遇,
整理得,9n=10k+3,
∴(k为正整数)
∴当k=6时,即n=6+1=7时,P、Q两点第二次在三角形ABC的顶点处相遇,
则t1=1+1.5(n﹣1)=10(秒),t2=25s
故答案为:25s.
三.解答题(每题8分,共72分)
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
18.已知:如图,AC=BD,AD=BC,AD,BC相交于点O,过点O作OE⊥AB,垂足为E.求证:
(1)△ABC≌△BAD.
(2)AE=BE.
证明(1)在ABC和△BAD中,
,
∴△ABC≌△BAD(SSS);
(2)∵△ABC≌△BAD,
∴∠CBA=∠DAB,
∴OA=OB,
∵OE⊥AB,
∴AE=BE.
19.在等边△ABC中,点D,E分别在边BC,AB上,且BE=CD,AD与CE交于点F.
求证:△AEC≌△BDA.
解:在等边三角形ABC中有:
AB=AC=BC,∠CAE=∠ABD,
∵BE=CD,
∴AB﹣BE=BC﹣CD,
即AE=BD,
在△AEC和△BDA中,
,
∴△AEC≌△BDA(SAS).
20.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=60°时,求∠EDF的度数.
(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:在△ABC中,AB=AC,∠A=60°,
∴∠B=∠C=60°,
∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B=60°,
∵DE=EF,
∴△DEF是等边三角形,
∴∠EDF=60°.
21.新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.求证:BD=CE.
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,点D、E均在△ABC外,连接BD、CE交于点M,连接AM,求证:AM平分∠BME.
证明:(1)∵△ABC和△ADE互为“兄弟三角形”,
∴∠BAC=∠DAE,AB=AC,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠CAE=∠BAD,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)如图,过点A作AG⊥DM于G,AH⊥EM于H,
∵△ABC和△ADE互为“兄弟三角形”,
∴∠BAC=∠DAE,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠CAE=∠BAD,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABG=∠ACH,
∵AG⊥BM,AH⊥EM,
∴∠AGB=∠AHC=90°,
又AB=AC,
∴△ABG≌△ACH(AAS),
∴AG=AH,
∵AG⊥DM,AH⊥EM,
∴AM平分∠BME.
22.在△ABC中,AB=AC,D是BC边的中点,E、F分别是AD、AC边上的点.
(1)如图①,连接BE、EF,若∠ABE=∠EFC,求证:BE=EF;
(2)如图②,若B、E、F在一条直线上,且∠ABE=∠BAC=45°,探究BD与AE的数量之间有何等量关系,并说明理由.
(1)证明:连接CE,
∵AB=AC,D是BC边的中点,
∴∠ABC=∠ACB,AD垂直平分BC,
∴BE=CE,
∴∠EBC=∠ECB,
∴∠ABC﹣∠EBC=∠ACB﹣∠ECB,
即∠ABE=∠ACE,
∵∠ABE=∠EFC,
∴∠ACE=∠EFC,
∴EF=CE,
∴BE=EF;
(2)AE=2BD,理由如下:
连接CE,
由(1)得,∠ABE=∠ACE,
∵∠ABE=∠BAC=45°,
∴△ABF和△CEF都是等腰直角三角形,
∴AF=BF,CF=EF,
在△CBF和△EAF中,
,
∴△CBF≌△EAF(SAS),
∴BC=AE,
∵BC=2BD,
∴AE=2BD.
23.如图,△ABC中,BD平分∠ABC,交AC于点D,AE⊥BD,垂足为点F.
(1)求证:AD=DE;
(2)若∠ABC=∠C=45°,求证:AD=EC.
证明:(1)∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵AE⊥BD,
∴∠AFB=∠EFB=90°,
在△ABF和△EBF中,
,
∴△ABF≌△EBF(ASA),
∴AF=EF,
∵AE⊥BD,
∴BD是AE的垂直平分线,
∴AD=DE;
(2)∵∠ABC=∠C=45°,
∴∠BAC=90°,
∵BD是AE的垂直平分线,
∴BA=BE,AD=DE,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(SSS),
∴∠BAD=∠BED=90°,
∴∠EDC=45°,
∴DE=EC,
∵AD=DE,
∴AD=EC.
24.如图,在△ACB中,AD为△ACB的角平分线,E为射线CB上的一点,过E点作EF⊥AB,垂足为F.
(1)若∠ACB=90°,当点E在线段CD上时,EF交AD于G点.
①如图1,求证:∠EGD=∠EDG.
②画∠CEF的角平分线分别交AC和BA的延长线于M,N点.请在图1中补全图形,并求证:∠MNA=∠CAD.
(2)如图2,若点E在CB延长线上,EP平分∠CEF交AD延长线于点P,试判断∠C与∠P的数量关系,并说明理由.
解:(1)证明:①∵AD为△ACB的角平分线,
∴∠CAD=∠BAD,
∵∠ACB=90°,
∴∠CDA+∠CAD=90°,
∵EF⊥AB,
∴∠AGF+∠BAD=90°,
∴∠CDA=∠AGF,
∵∠AGF=∠EGD,
∴∠EGD=∠EDG;
②∵NE平分∠CEF,
∴∠CEM=FEM,
∵∠CEF=∠EDG+∠EGD,
∴∠CEM+FEM=∠EDG+∠EGD,
∴∠CEM=∠EDG,
∴AD∥EN,
∴∠MNA=∠BAD,
∵∠BAD=∠CAD,
∴∠MNA=∠CAD;
(2)解:结论:2∠P﹣∠C=90°,
理由:设∠CAD=∠PAB=x,∠PEB=∠PEF=y,则有,
①×2﹣②得到,∠C=2∠P﹣90°,
∵2∠P﹣∠C=90°,
25.综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
(1)证明:∵∠BAC=∠DAE.
∴∠CAE=∠BAD.
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴∠AEC=∠ADB,
∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,
∵∠BFC+∠DFE=180°,
∴∠BFC=∠DAE=∠BAC=50°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.
∵△ACE≌△ABD,
∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD.
∴,
∴AJ=AH.
在Rt△AFJ和Rt△AFH中,
,
∴Rt△AFJ≌Rt△AFH(HL),
∴FJ=FH.
在Rt△AJE和Rt△AHD中,
,
∴Rt△AJE≌Rt△AHD(HL),
∴EJ=DH,
∴EF+DH=EF+EJ=FJ=FH.
第13章 全 等 三 角 形
时间:60分钟 总分:120分
一、选择题 (每题3分,共24分)
1.在等腰△ABC中有一个角是50°,那么另外两个角分别是 ( )
A.50°、80° B.50°、80°或 65°、65°
C.65°、65° D.无法确定
2.对假命题“若a>b,则a2>b2”举一个反例,符合要求的反例是( )
A.a=﹣1,b=﹣2 B.a=2,b=一1
C.a=2,b=1 D.a=﹣1,b=0
3.下列命题中,是假命题的是 ( )
A.对顶角相等
B.同旁内角互补
C.全等三角形的对应边相等
D.角平分线上的点到这个角的两边的距离相等
4.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,△ABC的周长为 ( )
A.16 B.13 C.19 D.10
5.用直尺和圆规作一个角的角平分线的示意图如图所示,其中说明△COE≌△DOE的依据是 ( )
A.SSS B.SAS C.ASA D.AAS
6.如图,在△ABC中,边AB,AC的垂直平分线交于点P,连接BP,CP,若∠A=50°,∠PBC= ( )
A.40° B.50° C.80° D.100°
7.如图,在△ABC中,以A为圆心,适当长为半径作弧,分别交AB、AC于点D、E,再分别以D、E为圆心,相同长为半径作弧,分别交DB、EC于点F、G,连接EF、DG,交于点H,连接AH并延长交BC于点I,则线段AI是( )
A.△ABC的高 B.△ABC的中线
C.△ABC的角平分线 D.以上都不对
8.如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为 ( )
A.54° B.50° C.48° D.46°
二.填空题(每题3分,共24分)
9.已知△ABC的三边长为x,3,6,△DEF的三边长为5,6,y.若△ABC与△DEF全等,则x+y的值为 .
10.如图,△ABC≌△DEF.点B、F、C、E在一条直线上,BE=5,BF=1,则CF= .
11.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=5,则OE的最小值为 .
12.如图,AB=AC,点D、E分别在AB、AC上,连接BE、CD.要使△ABE≌△ACD,则可添加的一个条件是 .
13.如图,在7×7的正方形网格中,A、B两点是格点,如果点C也是格点,且△ABC是等腰三角形,这样的C点有 个.
14.如图,已知∠A=13°,AB=BC=CD,那么∠BCD= 度.
15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于E,若AB=10,BC=7,AC=8,则△AEF的周长为 .
16.如图,等边三角形ABC的周长为30cm,P、Q两点分别从B、C两点同时出发,点P以6cm/s的速度按顺时针方向在三角形的边上运动,点Q以14cm/s的速度按逆时针方向在三角形的边上运动,设P、Q两点第一次在三角形ABC的顶点处相遇的时间为t1,第二次在三角形ABC顶点处相遇的时间为t2,则t2= .
三.解答题(每题8分,共72分)
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
18.已知:如图,AC=BD,AD=BC,AD,BC相交于点O,过点O作OE⊥AB,垂足为E.求证:
(1)△ABC≌△BAD.
(2)AE=BE.
19.在等边△ABC中,点D,E分别在边BC,AB上,且BE=CD,AD与CE交于点F.求证:△AEC≌△BDA.
20.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=60°时,求∠EDF的度数.
21.新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.求证:BD=CE.
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,点D、E均在△ABC外,连接BD、CE交于点M,连接AM,求证:AM平分∠BME.
22.在△ABC中,AB=AC,D是BC边的中点,E、F分别是AD、AC边上的点.
(1)如图①,连接BE、EF,若∠ABE=∠EFC,求证:BE=EF;
(2)如图②,若B、E、F在一条直线上,且∠ABE=∠BAC=45°,探究BD与AE的数量之间有何等量关系,并说明理由.
23.如图,△ABC中,BD平分∠ABC,交AC于点D,AE⊥BD,垂足为点F.
(1)求证:AD=DE;
(2)若∠ABC=∠C=45°,求证:AD=EC.
24.如图,在△ACB中,AD为△ACB的角平分线,E为射线CB上的一点,过E点作EF⊥AB,垂足为F.
(1)若∠ACB=90°,当点E在线段CD上时,EF交AD于G点.
①如图1,求证:∠EGD=∠EDG.
②画∠CEF的角平分线分别交AC和BA的延长线于M,N点.请在图1中补全图形,并求证:∠MNA=∠CAD.
(2)如图2,若点E在CB延长线上,EP平分∠CEF交AD延长线于点P,试判断∠C与∠P的数量关系,并说明理由.
25.综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
参考答案与试题解析
一.选择题(每题3分,共24分)
1.在等腰△ABC中有一个角是50°,那么另外两个角分别是( )
A.50°、80° B.50°、80°或 65°、65°
C.65°、65° D.无法确定
解:当∠B=50°为顶角时,
此时∠A=∠C==65°;
当∠B=50°为底角时,
此时另一底角为50°,顶角为80°,
故另外两个角分别是50°,80°或65°,65°.
故选:B.
2.对假命题“若a>b,则a2>b2”举一个反例,符合要求的反例是( )
A.a=﹣1,b=﹣2 B.a=2,b=一1 C.a=2,b=1 D.a=﹣1,b=0
解:当a=﹣1,b=﹣2时,a>b,而a2<b2,
∴“若a>b,则a2>b2”是假命题,
故选:A.
3.下列命题中,是假命题的是( )
A.对顶角相等
B.同旁内角互补
C.全等三角形的对应边相等
D.角平分线上的点到这个角的两边的距离相等
解:A、对顶角相等,本选项说法是真命题,不符合题意;
B、两直线平行,同旁内角互补,故本选项说法是假命题,符合题意;
C、全等三角形的对应边相等,本选项说法是真命题,不符合题意;
D、角平分线上的点到这个角的两边的距离相等,本选项说法是真命题,不符合题意;
故选:B.
4.如图,在△ABC中,DE是AC的垂直平分线,AE=3,△ABD的周长为13,△ABC的周长为( )
A.16 B.13 C.19 D.10
解:∵DE是AC的垂直平分线,AE=3,
∴DA=DC,AC=2AE=6,
∵△ABD的周长为13,
∴AB+BD+AD=AB+BD+DC=AB+BC=13,
∴△ABC的周长=AB+BC+AC=13+6=19,
故选:C.
5.用直尺和圆规作一个角的角平分线的示意图如图所示,其中说明△COE≌△DOE的依据是( )
A.SSS B.SAS C.ASA D.AAS
解:根据作图的过程可知:
OC=OD,CE=DE,OE=OE
∴△OCE≌△ODE(SSS)
∴∠COE=∠DOE
故选:A.
6.如图,在△ABC中,边AB,AC的垂直平分线交于点P,连接BP,CP,若∠A=50°,∠PBC=( )
A.40° B.50° C.80° D.100°
解:连接AP,
在△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵边AB,AC的垂直平分线交于点P,
∴PA=PB,PA=PC,
∴∠PAB=∠PBA,∠PAC=∠PCA,PB=PC,
∴∠PBA+∠PCA=∠PAB+∠PAC=50°,
∴∠PBC+∠PCB=130°﹣50°=80°,
∵PB=PC,
∴∠PBC=∠PCB=40°,
故选:A.
7.如图,在△ABC中,以A为圆心,适当长为半径作弧,分别交AB、AC于点D、E,再分别以D、E为圆心,相同长为半径作弧,分别交DB、EC于点F、G,连接EF、DG,交于点H,连接AH并延长交BC于点I,则线段AI是( )
A.△ABC的高 B.△ABC的中线
C.△ABC的角平分线 D.以上都不对
解:由作图可知,AE=AD,AG=AF,
在△AFE和△AGD中,
,
∴△AFE≌△AGD(SAS),
∴∠AFE=∠AGD,
∵AG=AF,AE=AD,
∴EG=DF,
在△EHG和△DHF中,
,
∴△EHG≌△DHF(AAS),
∴EH=DH,
在△AHE和△AHD中,
,
∴△AHE≌△AHD(SSS),
∴∠EAH=∠DAH,
∴AI是△ABC的角平分线.
故选:C.
8.如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )
A.54° B.50° C.48° D.46°
解:如图所示,过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DF=DE,
又∵∠ACD=136°,∠BCD=44°,
∴∠ACB=92°,∠DCF=44°,
∴CD平分∠BCF,
又∵DF⊥AC于F,DG⊥BC于G,
∴DF=DG,
∴DE=DG,
∴BD平分∠CBE,
∴∠DBE=∠CBE,
∵AD平分∠BAC,
∴∠BAD=∠BAC,
∴∠ADB=∠DBE﹣∠BAD=(∠CBE﹣∠BAC)=∠ACB=×92°=46°,
故选:D.
二.填空题(每题3分,共24分)
9.已知△ABC的三边长为x,3,6,△DEF的三边长为5,6,y.若△ABC与△DEF全等,则x+y的值为 8 .
解:因为△ABC与△DEF全等,
所以x=5,y=3,
所以x+y=8,
故答案为:8.
10.如图,△ABC≌△DEF.点B、F、C、E在一条直线上,BE=5,BF=1,则CF= 3 .
解:∵△ABC≌△DEF,
∴BC=EF,
∴BF=EC=1,
∴FC=BE﹣BF﹣EC=5﹣1﹣1=3.
故答案为:3.
11.如图,BO平分∠ABC,OD⊥BC于点D,点E为射线BA上一动点,若OD=5,则OE的最小值为 5 .
解:∵BO平分∠ABC,OD⊥BC于点D,OD=5,
∴O到AB的距离等于OD的长,
根据垂线段最短,可知OE最小值为5.
故答案为:5.
12.如图,AB=AC,点D、E分别在AB、AC上,连接BE、CD.要使△ABE≌△ACD,则可添加的一个条件是 ∠B=∠C .
解:在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA).
故答案为:∠B=∠C.(答案不唯一).
13.如图,在7×7的正方形网格中,A、B两点是格点,如果点C也是格点,且△ABC是等腰三角形,这样的C点有 8 个.
解:以A为圆心,AB的长为半径作圆,此时C点有4个,
以B为圆心,AB的长为半径作圆,此时C点有4个,
作AB的垂直平分线,此时C点有0个,
故答案为:8.
14.如图,已知∠A=13°,AB=BC=CD,那么∠BCD= 128 度.
解:∵AB=BC,
∴∠BCA=∠A=13°,
∴∠CBD=∠A+∠BCD=26°,
又∵BC=CD,
∴∠CBD=∠D=26°,
∴∠BCD=180°﹣∠CBD﹣∠D=128°.
故答案为:128.
15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E,交AC于E,若AB=10,BC=7,AC=8,则△AEF的周长为 18 .
解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵BD平分∠ABC,CD平分∠ACB,
∴∠ABD=∠DBC,∠ACD=∠DCB,
∴∠ABD=∠EDB,∠ACD=∠FDC,
∴EB=ED,FD=FC,
∴△AEF的周长=AE+EF+AF
=AE+ED+DF+AF
=AE+BE+CF+AF
=AB+AC
=10+8
=18,
故答案为:18.
16.如图,等边三角形ABC的周长为30cm,P、Q两点分别从B、C两点同时出发,点P以6cm/s的速度按顺时针方向在三角形的边上运动,点Q以14cm/s的速度按逆时针方向在三角形的边上运动,设P、Q两点第一次在三角形ABC的顶点处相遇的时间为t1,第二次在三角形ABC顶点处相遇的时间为t2,则t2= 25s .
解:∵等边三角形ABC的周长为30cm,
∴△ABC的边长为10cm,
由题意知,P、Q第一次时间为20÷(6+14)=1(秒)
以后每隔30÷(6+14)=1.5秒,P、Q就会相遇一次,
设P、Q相遇次数为n次,则
当6×1+6×1.5(n﹣1)=10k(k为正整数)时,P、Q两点就在三角形ABC的顶点处相遇,
整理得,9n=10k+3,
∴(k为正整数)
∴当k=6时,即n=6+1=7时,P、Q两点第二次在三角形ABC的顶点处相遇,
则t1=1+1.5(n﹣1)=10(秒),t2=25s
故答案为:25s.
三.解答题(每题8分,共72分)
17.如图,已知AD平分∠BAC,AB=AC.求证:△ABD≌△ACD.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
18.已知:如图,AC=BD,AD=BC,AD,BC相交于点O,过点O作OE⊥AB,垂足为E.求证:
(1)△ABC≌△BAD.
(2)AE=BE.
证明(1)在ABC和△BAD中,
,
∴△ABC≌△BAD(SSS);
(2)∵△ABC≌△BAD,
∴∠CBA=∠DAB,
∴OA=OB,
∵OE⊥AB,
∴AE=BE.
19.在等边△ABC中,点D,E分别在边BC,AB上,且BE=CD,AD与CE交于点F.
求证:△AEC≌△BDA.
解:在等边三角形ABC中有:
AB=AC=BC,∠CAE=∠ABD,
∵BE=CD,
∴AB﹣BE=BC﹣CD,
即AE=BD,
在△AEC和△BDA中,
,
∴△AEC≌△BDA(SAS).
20.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=60°时,求∠EDF的度数.
(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:在△ABC中,AB=AC,∠A=60°,
∴∠B=∠C=60°,
∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B=60°,
∵DE=EF,
∴△DEF是等边三角形,
∴∠EDF=60°.
21.新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.
(1)如图1,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点.求证:BD=CE.
(2)如图2,△ABC和△ADE互为“兄弟三角形”,点A为重合的顶角顶点,点D、E均在△ABC外,连接BD、CE交于点M,连接AM,求证:AM平分∠BME.
证明:(1)∵△ABC和△ADE互为“兄弟三角形”,
∴∠BAC=∠DAE,AB=AC,AD=AE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠CAE=∠BAD,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE;
(2)如图,过点A作AG⊥DM于G,AH⊥EM于H,
∵△ABC和△ADE互为“兄弟三角形”,
∴∠BAC=∠DAE,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠CAE=∠BAD,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABG=∠ACH,
∵AG⊥BM,AH⊥EM,
∴∠AGB=∠AHC=90°,
又AB=AC,
∴△ABG≌△ACH(AAS),
∴AG=AH,
∵AG⊥DM,AH⊥EM,
∴AM平分∠BME.
22.在△ABC中,AB=AC,D是BC边的中点,E、F分别是AD、AC边上的点.
(1)如图①,连接BE、EF,若∠ABE=∠EFC,求证:BE=EF;
(2)如图②,若B、E、F在一条直线上,且∠ABE=∠BAC=45°,探究BD与AE的数量之间有何等量关系,并说明理由.
(1)证明:连接CE,
∵AB=AC,D是BC边的中点,
∴∠ABC=∠ACB,AD垂直平分BC,
∴BE=CE,
∴∠EBC=∠ECB,
∴∠ABC﹣∠EBC=∠ACB﹣∠ECB,
即∠ABE=∠ACE,
∵∠ABE=∠EFC,
∴∠ACE=∠EFC,
∴EF=CE,
∴BE=EF;
(2)AE=2BD,理由如下:
连接CE,
由(1)得,∠ABE=∠ACE,
∵∠ABE=∠BAC=45°,
∴△ABF和△CEF都是等腰直角三角形,
∴AF=BF,CF=EF,
在△CBF和△EAF中,
,
∴△CBF≌△EAF(SAS),
∴BC=AE,
∵BC=2BD,
∴AE=2BD.
23.如图,△ABC中,BD平分∠ABC,交AC于点D,AE⊥BD,垂足为点F.
(1)求证:AD=DE;
(2)若∠ABC=∠C=45°,求证:AD=EC.
证明:(1)∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵AE⊥BD,
∴∠AFB=∠EFB=90°,
在△ABF和△EBF中,
,
∴△ABF≌△EBF(ASA),
∴AF=EF,
∵AE⊥BD,
∴BD是AE的垂直平分线,
∴AD=DE;
(2)∵∠ABC=∠C=45°,
∴∠BAC=90°,
∵BD是AE的垂直平分线,
∴BA=BE,AD=DE,
在△ABD和△EBD中,
,
∴△ABD≌△EBD(SSS),
∴∠BAD=∠BED=90°,
∴∠EDC=45°,
∴DE=EC,
∵AD=DE,
∴AD=EC.
24.如图,在△ACB中,AD为△ACB的角平分线,E为射线CB上的一点,过E点作EF⊥AB,垂足为F.
(1)若∠ACB=90°,当点E在线段CD上时,EF交AD于G点.
①如图1,求证:∠EGD=∠EDG.
②画∠CEF的角平分线分别交AC和BA的延长线于M,N点.请在图1中补全图形,并求证:∠MNA=∠CAD.
(2)如图2,若点E在CB延长线上,EP平分∠CEF交AD延长线于点P,试判断∠C与∠P的数量关系,并说明理由.
解:(1)证明:①∵AD为△ACB的角平分线,
∴∠CAD=∠BAD,
∵∠ACB=90°,
∴∠CDA+∠CAD=90°,
∵EF⊥AB,
∴∠AGF+∠BAD=90°,
∴∠CDA=∠AGF,
∵∠AGF=∠EGD,
∴∠EGD=∠EDG;
②∵NE平分∠CEF,
∴∠CEM=FEM,
∵∠CEF=∠EDG+∠EGD,
∴∠CEM+FEM=∠EDG+∠EGD,
∴∠CEM=∠EDG,
∴AD∥EN,
∴∠MNA=∠BAD,
∵∠BAD=∠CAD,
∴∠MNA=∠CAD;
(2)解:结论:2∠P﹣∠C=90°,
理由:设∠CAD=∠PAB=x,∠PEB=∠PEF=y,则有,
①×2﹣②得到,∠C=2∠P﹣90°,
∵2∠P﹣∠C=90°,
25.综合与探究
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.
(1)求证:△ACE≌△ABD.
(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.
(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.
(1)证明:∵∠BAC=∠DAE.
∴∠CAE=∠BAD.
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS);
(2)解:∵△ACE≌△ABD,
∴∠AEC=∠ADB,
∴∠AEF+∠AEC=∠AEF+∠ADB=180°.
∴∠DAE+∠DFE=180°,
∵∠BFC+∠DFE=180°,
∴∠BFC=∠DAE=∠BAC=50°;
(3)证明:如图,连接AF,过点A作AJ⊥CF于点J.
∵△ACE≌△ABD,
∴S△ACE=S△ABD,CE=BD,
∵AJ⊥CE,AH⊥BD.
∴,
∴AJ=AH.
在Rt△AFJ和Rt△AFH中,
,
∴Rt△AFJ≌Rt△AFH(HL),
∴FJ=FH.
在Rt△AJE和Rt△AHD中,
,
∴Rt△AJE≌Rt△AHD(HL),
∴EJ=DH,
∴EF+DH=EF+EJ=FJ=FH.
