人教版(新)八上-12.1 全等三角形【优质课件】
文档属性
| 名称 | 人教版(新)八上-12.1 全等三角形【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
12.1 全等三角形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
观察这些图片,你能看出形状、大小完全一样的几何图形吗?
追问 你能再举出生活中的一些类似例子吗?
新课精讲
探索新知
1
知识点
全等形
探索新知
探索新知
形状、大小相同的图形放在一起能够完全重合.能够完全重合 的两个图形叫做全等形.
定义:
一个图形经过平移,翻折,旋转后,位置变化了,但 _______
和_____ 都没有改变,即平移,翻折,旋转前后的图形__________ .
完全重合
形状
大小
探索新知
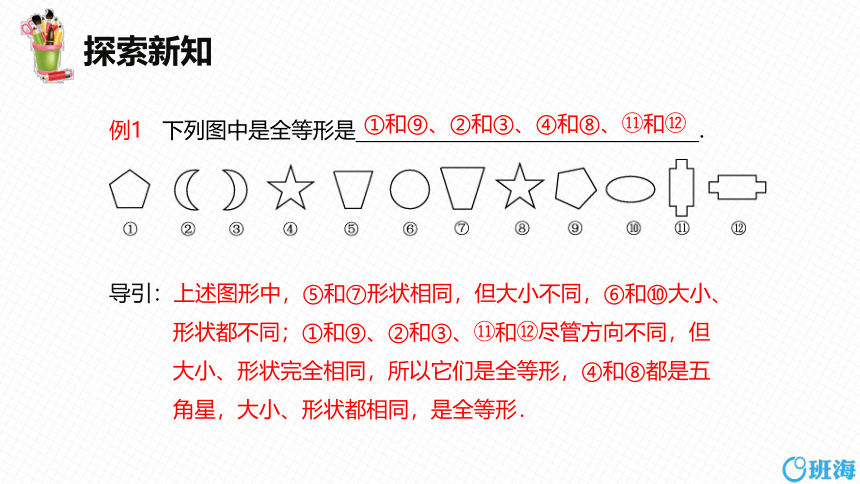
例1 下列图中是全等形是 .
①和⑨、②和③、④和⑧、 和
导引:上述图形中,⑤和⑦形状相同,但大小不同,⑥和⑩大小、
形状都不同;①和⑨、②和③、 和 尽管方向不同,但
大小、形状完全相同,所以它们是全等形,④和⑧都是五
角星,大小、形状都相同,是全等形.
探索新知
总 结
(1)此题运用定义识别全等形,确定两个图形全等要符合两
个条件:①形状相同,②大小相等;是否是全等形与位
置无关.
(2)判断两个全等形还可以通过平移、旋转、翻折等方法把
两个图形叠合在一起,看它们能否完全重合,即用叠合
法判断.
典题精讲
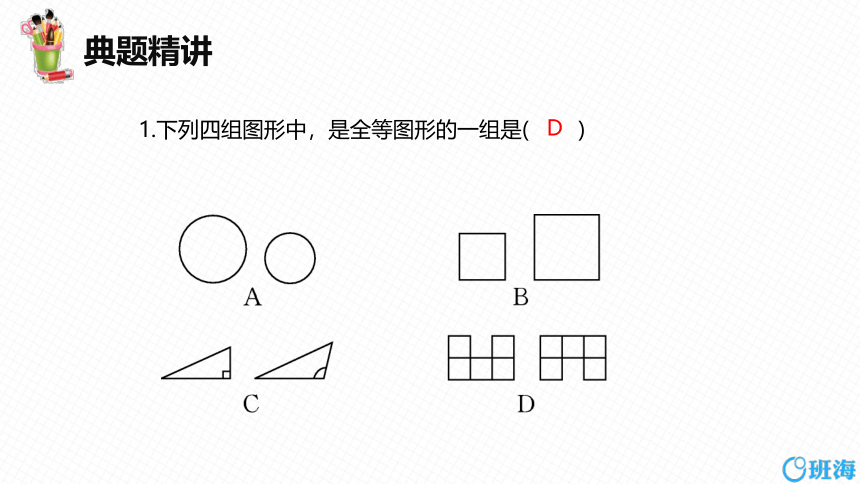
1.下列四组图形中,是全等图形的一组是( )
D
典题精讲
2.如图,有6个条形方格图,图中由实线围成的图形中,全等形有:
(1)与____________;(2)与____________.
(6)
(3)
(5)
典题精讲
3.下列说法,其中正确的个数为( )
①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;
③面积相等的两个图形全等;
④周长相等的两个图形全等.
A.1个 B.2个 C.3个 D.4个
B
探索新知
2
知识点
全等三角形及对应元素
A
B
C
E
D
F
例如
能够完全重合的两个三角形,叫做_________________.
全等三角形
探索新知
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
探索新知
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
A
B
C
E
D
F
探索新知
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB,
写出其对应边和对应角.
导引:在△ABD和△CDB中,∠ABD=∠CDB,则∠ABD,∠CDB
所对的边AD与CB是对应边,公共边BD与DB是对应边,
余下的一对边AB与CD是对应边.由对应边所对的角是对
应角可确定其他两组对应角.
解:BD与DB,AD与CB,AB与CD是对应边;∠A与∠C,∠ABD
与∠CDB,∠ADB与∠CBD是对应角.
对应元素的确定方法:
(1)字母顺序确定法:根据书写规范,按照对应顶点确定对应边、对应角,如△CAB≌△FDE,则AB与DE、AC与DF、BC与EF是对应边,∠A和∠D、∠B和∠E、∠C和∠F是对应角;
(2)图形位置确定法:①公共边一定是对应边,②公共角一定是
对应角;③对顶角一定是对应角;
(3)图形大小确定法:两个全等三角形的最大的边(角)是对应边
(角),最小的边(角)是对应边(角).
探索新知
总 结
典题精讲
1.说出图12.1-2 (2)、图12.1-2 (3)中两个全等三角形 的对应边、对应角.
解:在教材图12.1 2(2)中,AB和DB,
BC和BC,AC和DC是对应边;
∠A和∠D,∠ABC和∠DBC,
∠ACB和∠DCB是对应角.
在教材图12.1 2(3)中,AB和AD,BC和DE,AC和AE是对应边;
∠BAC和∠DAE,∠B和∠D,∠C和∠E是对应角.
图 12.1-2
典题精讲
2.如图,将△ABC沿BC所在的直线平移到△A′B′C′的位置,则
△ABC________△A′B′C′,图中∠A与______ ,∠C与________ ,
∠ABC与___________是对应角.
≌
∠A′
∠ A′B′C′
∠C′
探索新知
3
知识点
全等三角形的性质
图12.1-2(中),△ABC≌△DEF,对应边有什么关系?对应角有什么关系?
图12.1-2
探索新知
还具备:全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
全等三角形的对应边相等,
全等三角形的对应角相等。
全等三角形的性质
探索新知
例3 如图,已知点A,D,B,F在同一条直线上,
△ABC≌△FDE,AB=8 cm,BD=6 cm.
求FB的长.
导引:由全等三角形的性质知AB=FD,由等式的性质可得AD
=FB,所以要求FB的长,只需求AD的长.
解:∵△ABC≌△FDE,∴ AB=FD.
∴ AB-DB=FD-DB,即AD=FB. ∵AB=8 cm,BD=6 cm,
∴AD=AB-DB=8-6= 2(cm).
∴FB=AD=2cm.
探索新知
在应用全等三角形性质时,要先确定两个条件:
①两个三角形全等;②找对应元素;
全等三角形的性质是证明线段、角相等的常用方法.
总 结
典题精讲
1.如图,△OCA≌△OBD,点C和点B,点A和点D 对应顶点. 说出
这两个三角形中相等的边和角.
解:相等的边:AC=DB,OA=OD,OC=OB;
相等的角:∠A=∠D,∠C=∠B,
∠AOC=∠DOB.
典题精讲
2.若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,
则下列结论错误的是( )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
A
学以致用
小试牛刀
1.能够____________的两个图形叫做全等形;平移、翻折、旋转
前后的两个图形________.
完全重合
全等
2.能够完全________的两个三角形叫做全等三角形;把两个全等
的三角形重合到一起,重合的顶点叫做__________ ,重合的边
叫做________ ,重合的角叫做__________.
重合
对应顶点
对应边
对应角
小试牛刀
3.全等用符号“_____”表示,读作“________”.记两个三角形全
等时,通常把表示对应顶点的字母写在________的位置上.
≌
全等于
对应
4.全等三角形是两个能够完全重合的三角形,因此它们的________
边相等,________角相等.
对应
对应
小试牛刀
5.下列图形(如图)中,是全等形的有( )
A.4对 B.3对 C.2对 D.1对
B
小试牛刀
6.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列
表示正确的是( )
A.△ABC≌△AED
B.△ABC≌△EAD
C.△ABC≌△DEA
D.△ABC≌△ADE
D
小试牛刀
7.如图,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′
处,此时,点A的对应点A′恰好落在BC的延长线上,下列
结论错误的是( )
A.∠BCB′=∠ACA′
B.∠ACB=2∠B
C.∠B′CA=∠B′AC
D.B′C平分∠BB′A′
C
小试牛刀
8.如图,Rt△ABE≌Rt△ECD,点B,E,C在同一直线上,则
以下结论:①AE=ED;②AE⊥ED;③BC=AB+CD;
④AB∥DC.其中成立的是( )
A.①
B.①③
C.①③④
D.①②③④
D
小试牛刀
9.如图,A,D,E三点在同一直线上,
且△BAD≌△ACE.
(1)求证BD=DE+CE.
分析:要证明BD=DE+CE,实质是看是否能将BD分割成DE,CE两线段;由图知这很难实现,因此我们可以考虑将与BD相等的线段分割成DE,CE两段.
证明:∵△BAD≌△ACE,∴AD=CE,BD=AE.
∵AE=AD+DE,∴BD=DE+CE.
小试牛刀
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
分析:要使BD∥CE,则需∠BDE=∠CEA,
而由△BAD≌△ACE可知∠ADB=∠CEA,
由此可得结果.
解:当△ABD满足∠ADB=90°时,BD∥CE.
∵△BAD≌△ACE,∴∠ADB=∠CEA=90°.
易知∠ADB=∠BDE=90°,
∴∠CEA=∠BDE=90°. ∴BD∥CE.
课堂小结
课堂小结
1. 回忆全等三角形定义,记法与性质.
2.归纳寻找对应边, 对应角的规律:
(1)全等三角形对应角所对的边是对应边,两个对应所夹的边是对应边;对应边所对的角是对应角, 两条对应边的夹角是对应角.
(2)公共边一般是对应边;有对顶角的,对顶角一般是对应角;公共角一般是对应角等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
12.1 全等三角形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
观察这些图片,你能看出形状、大小完全一样的几何图形吗?
追问 你能再举出生活中的一些类似例子吗?
新课精讲
探索新知
1
知识点
全等形
探索新知
探索新知
形状、大小相同的图形放在一起能够完全重合.能够完全重合 的两个图形叫做全等形.
定义:
一个图形经过平移,翻折,旋转后,位置变化了,但 _______
和_____ 都没有改变,即平移,翻折,旋转前后的图形__________ .
完全重合
形状
大小
探索新知
例1 下列图中是全等形是 .
①和⑨、②和③、④和⑧、 和
导引:上述图形中,⑤和⑦形状相同,但大小不同,⑥和⑩大小、
形状都不同;①和⑨、②和③、 和 尽管方向不同,但
大小、形状完全相同,所以它们是全等形,④和⑧都是五
角星,大小、形状都相同,是全等形.
探索新知
总 结
(1)此题运用定义识别全等形,确定两个图形全等要符合两
个条件:①形状相同,②大小相等;是否是全等形与位
置无关.
(2)判断两个全等形还可以通过平移、旋转、翻折等方法把
两个图形叠合在一起,看它们能否完全重合,即用叠合
法判断.
典题精讲
1.下列四组图形中,是全等图形的一组是( )
D
典题精讲
2.如图,有6个条形方格图,图中由实线围成的图形中,全等形有:
(1)与____________;(2)与____________.
(6)
(3)
(5)
典题精讲
3.下列说法,其中正确的个数为( )
①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;
③面积相等的两个图形全等;
④周长相等的两个图形全等.
A.1个 B.2个 C.3个 D.4个
B
探索新知
2
知识点
全等三角形及对应元素
A
B
C
E
D
F
例如
能够完全重合的两个三角形,叫做_________________.
全等三角形
探索新知
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
探索新知
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
A
B
C
E
D
F
探索新知
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB,
写出其对应边和对应角.
导引:在△ABD和△CDB中,∠ABD=∠CDB,则∠ABD,∠CDB
所对的边AD与CB是对应边,公共边BD与DB是对应边,
余下的一对边AB与CD是对应边.由对应边所对的角是对
应角可确定其他两组对应角.
解:BD与DB,AD与CB,AB与CD是对应边;∠A与∠C,∠ABD
与∠CDB,∠ADB与∠CBD是对应角.
对应元素的确定方法:
(1)字母顺序确定法:根据书写规范,按照对应顶点确定对应边、对应角,如△CAB≌△FDE,则AB与DE、AC与DF、BC与EF是对应边,∠A和∠D、∠B和∠E、∠C和∠F是对应角;
(2)图形位置确定法:①公共边一定是对应边,②公共角一定是
对应角;③对顶角一定是对应角;
(3)图形大小确定法:两个全等三角形的最大的边(角)是对应边
(角),最小的边(角)是对应边(角).
探索新知
总 结
典题精讲
1.说出图12.1-2 (2)、图12.1-2 (3)中两个全等三角形 的对应边、对应角.
解:在教材图12.1 2(2)中,AB和DB,
BC和BC,AC和DC是对应边;
∠A和∠D,∠ABC和∠DBC,
∠ACB和∠DCB是对应角.
在教材图12.1 2(3)中,AB和AD,BC和DE,AC和AE是对应边;
∠BAC和∠DAE,∠B和∠D,∠C和∠E是对应角.
图 12.1-2
典题精讲
2.如图,将△ABC沿BC所在的直线平移到△A′B′C′的位置,则
△ABC________△A′B′C′,图中∠A与______ ,∠C与________ ,
∠ABC与___________是对应角.
≌
∠A′
∠ A′B′C′
∠C′
探索新知
3
知识点
全等三角形的性质
图12.1-2(中),△ABC≌△DEF,对应边有什么关系?对应角有什么关系?
图12.1-2
探索新知
还具备:全等三角形对应边上的中线相等,对应边上的高相等,对应角平分线相等;全等三角形的周长相等、面积也相等.
全等三角形的对应边相等,
全等三角形的对应角相等。
全等三角形的性质
探索新知
例3 如图,已知点A,D,B,F在同一条直线上,
△ABC≌△FDE,AB=8 cm,BD=6 cm.
求FB的长.
导引:由全等三角形的性质知AB=FD,由等式的性质可得AD
=FB,所以要求FB的长,只需求AD的长.
解:∵△ABC≌△FDE,∴ AB=FD.
∴ AB-DB=FD-DB,即AD=FB. ∵AB=8 cm,BD=6 cm,
∴AD=AB-DB=8-6= 2(cm).
∴FB=AD=2cm.
探索新知
在应用全等三角形性质时,要先确定两个条件:
①两个三角形全等;②找对应元素;
全等三角形的性质是证明线段、角相等的常用方法.
总 结
典题精讲
1.如图,△OCA≌△OBD,点C和点B,点A和点D 对应顶点. 说出
这两个三角形中相等的边和角.
解:相等的边:AC=DB,OA=OD,OC=OB;
相等的角:∠A=∠D,∠C=∠B,
∠AOC=∠DOB.
典题精讲
2.若△ABC与△DEF全等,点A和点E,点B和点D分别是对应点,
则下列结论错误的是( )
A.BC=EF
B.∠B=∠D
C.∠C=∠F
D.AC=EF
A
学以致用
小试牛刀
1.能够____________的两个图形叫做全等形;平移、翻折、旋转
前后的两个图形________.
完全重合
全等
2.能够完全________的两个三角形叫做全等三角形;把两个全等
的三角形重合到一起,重合的顶点叫做__________ ,重合的边
叫做________ ,重合的角叫做__________.
重合
对应顶点
对应边
对应角
小试牛刀
3.全等用符号“_____”表示,读作“________”.记两个三角形全
等时,通常把表示对应顶点的字母写在________的位置上.
≌
全等于
对应
4.全等三角形是两个能够完全重合的三角形,因此它们的________
边相等,________角相等.
对应
对应
小试牛刀
5.下列图形(如图)中,是全等形的有( )
A.4对 B.3对 C.2对 D.1对
B
小试牛刀
6.如图,已知∠1=∠2,∠B=∠D,△ABC和△EAD全等,则下列
表示正确的是( )
A.△ABC≌△AED
B.△ABC≌△EAD
C.△ABC≌△DEA
D.△ABC≌△ADE
D
小试牛刀
7.如图,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′
处,此时,点A的对应点A′恰好落在BC的延长线上,下列
结论错误的是( )
A.∠BCB′=∠ACA′
B.∠ACB=2∠B
C.∠B′CA=∠B′AC
D.B′C平分∠BB′A′
C
小试牛刀
8.如图,Rt△ABE≌Rt△ECD,点B,E,C在同一直线上,则
以下结论:①AE=ED;②AE⊥ED;③BC=AB+CD;
④AB∥DC.其中成立的是( )
A.①
B.①③
C.①③④
D.①②③④
D
小试牛刀
9.如图,A,D,E三点在同一直线上,
且△BAD≌△ACE.
(1)求证BD=DE+CE.
分析:要证明BD=DE+CE,实质是看是否能将BD分割成DE,CE两线段;由图知这很难实现,因此我们可以考虑将与BD相等的线段分割成DE,CE两段.
证明:∵△BAD≌△ACE,∴AD=CE,BD=AE.
∵AE=AD+DE,∴BD=DE+CE.
小试牛刀
(2)当△ABD满足什么条件时,BD∥CE?并说明理由.
分析:要使BD∥CE,则需∠BDE=∠CEA,
而由△BAD≌△ACE可知∠ADB=∠CEA,
由此可得结果.
解:当△ABD满足∠ADB=90°时,BD∥CE.
∵△BAD≌△ACE,∴∠ADB=∠CEA=90°.
易知∠ADB=∠BDE=90°,
∴∠CEA=∠BDE=90°. ∴BD∥CE.
课堂小结
课堂小结
1. 回忆全等三角形定义,记法与性质.
2.归纳寻找对应边, 对应角的规律:
(1)全等三角形对应角所对的边是对应边,两个对应所夹的边是对应边;对应边所对的角是对应角, 两条对应边的夹角是对应角.
(2)公共边一般是对应边;有对顶角的,对顶角一般是对应角;公共角一般是对应角等.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
