人教版(新)八上-12.2 三角形全等的判定 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-12.2 三角形全等的判定 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览








文档简介
(共32张PPT)
12.2
三角形全等的判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1. 什么是全等三角形?
2. 我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS)和边角边(SAS).
新课精讲
探索新知
1
知识点
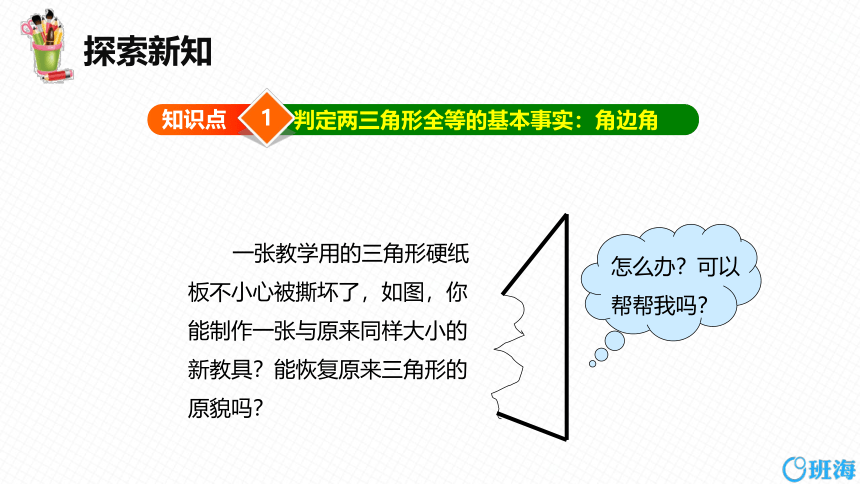
判定两三角形全等的基本事实:角边角
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复原来三角形的原貌吗?
怎么办?可以帮帮我吗?
探索新知
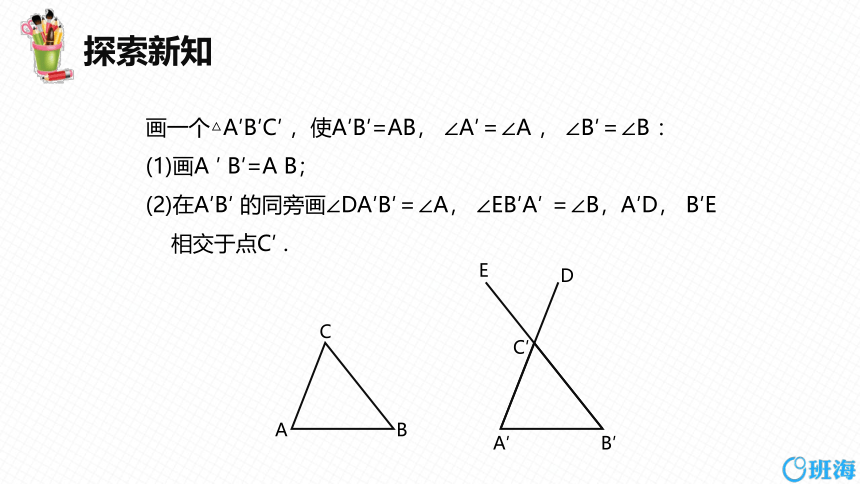
画一个△A′B′C′ ,使A′B′=AB, ∠A′=∠A , ∠B′=∠B :
(1)画A ′ B′=A B;
(2)在A′B′ 的同旁画∠DA′B′=∠A, ∠EB′A′ =∠B,A′D, B′E
相交于点C′ .
A′
B′
C′
D
E
C
A
B
探索新知
归 纳
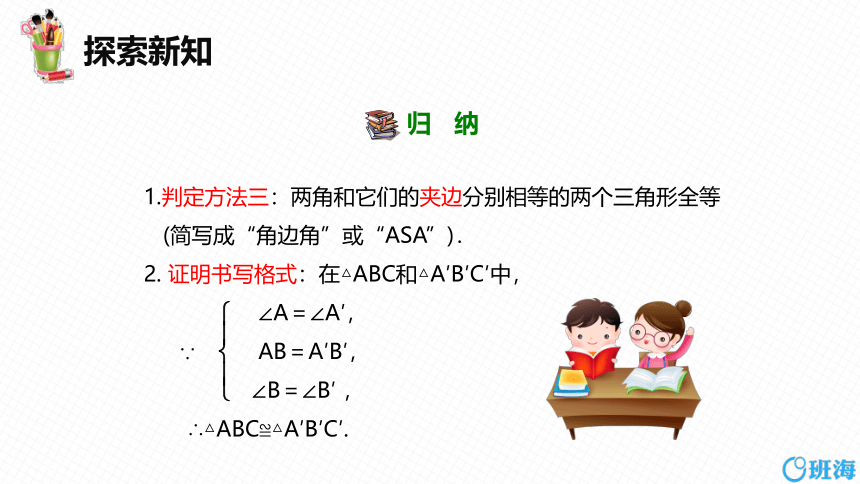
1.判定方法三:两角和它们的夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”).
2. 证明书写格式:在△ABC和△A′B′C′中,
∠A=∠A′,
AB=A′B′,
∠B=∠B′ ,
∴△ABC≌△A′B′C′.
∵
探索新知
例1 已知:如图,点D在AB上,点E在AC上,AB=AC,
∠B=∠C,求证:AD=AE.
AC=AB ,
∠C=∠B ,
∴△ACD≌△ABE(ASA).
∴AD=AE.
分析:证明△ACD≌△ABE中,就可以得出AD=AE.
∠A=∠A(公共角),
证明:在△ACD和△ABE中,
B
C
A
D
E
探索新知
总 结
在证两三角形全等所需要的角相等时,目前通常采用的方法有:
(1)公共角、对顶角分别相等;
(2)等角加(减) 等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等; (4)角平分线得到相等角;
(5)平行线的同位角、内错角相等; (6)直角都相等;
(7)全等三角形对应角相等; (8)第三角代换,即等量代换等.
典题精讲
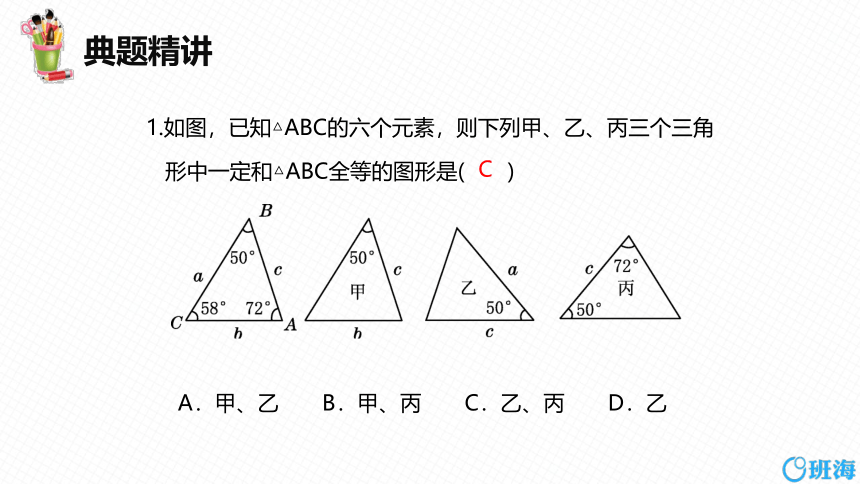
1.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角
形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙 C.乙、丙 D.乙
C
典题精讲
2.如图,某同学不小心把一块三角形玻璃打碎成三块,现在要到
玻璃店配一块与原来完全相同的玻璃,最省事的方法是( )
A.带(1)和(2)去
B.只带(2)去
C.只带(3)去
D.都带去
C
典题精讲
3.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件
后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
B
典题精讲
4.如图,AB ⊥ BC, AD ⊥ DC,垂足分别为
B,D, ∠1 = ∠2.求证AB=AD.
证明: ∵ AB⊥BC,AD⊥DC, ∴∠B=∠D=90°.
在△ABC和△ADC中,
∠B=∠D,
∠1=∠2,
AC= AC (公共边),
∴△ABC≌△ADC(AAS). ∴ AB=AD(全等三角形的对应边相等).
C
B
D
A
1
2
探索新知
2
知识点
判定两三角形全等的推论:角角边
例2 如图,AD是△ABC的中线,过C,B分别作AD及
AD的延长线的垂线CF,BE.求证:BE=CF.
导引:要证明BE=CF,可根据中线及垂线的定义和对顶角的性质来证明△BDE和△CDF全等.
探索新知
证明:∵AD是△ABC的中线,∴BD=CD.
∵CF⊥AD,BE⊥AE,∴∠CFD=∠BED=90°.
在△BDE和△CDF中,
∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BDE≌△CDF(AAS).∴BE=CF.
探索新知
总 结
判定两三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法看缺什么条件,再去证什么条件,简言之:即综合利用分析法和综合法寻找证明途径.
典题精讲
1.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC
≌△DCB的是( )
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD
D
典题精讲
2.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=
∠ACD=90°,且BC=CE. 求证:△ABC与△DEC全等.
证明: ∵∠BCE=∠ACD=90°, ∴∠3+∠4=∠4+∠5,
∴∠3=∠5,在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,∵∠BAE=∠1+∠2=90°,
∴∠1=∠D, 在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
学以致用
小试牛刀
1.________和它们的________分别相等的两个三角形全等,可以
简写成“_________”或“______”.如图,已知
两角
夹边
角边角
ASA
∠A
∠D
2._______分别相等且其中一组_______的_______相等的两个三角
形全等,可以简写成“___________”或“________”.
两角
等角
对边
角角边
AAS
AO=DO,∠AOB与∠DOC是对顶角,
还需补充条件______=______,就可根
据“ASA”证明△AOB≌△DOC.
小试牛刀
3.如图,∠B=∠DEF,AB=DE,要判断△ABC≌△DEF,
(1)若以“ASA”为依据,还需添加的条件为
________________ ;
(2)若以“AAS”为依据,还需添加的条
件为_______________________.
∠A=∠D
∠ACB=∠F(或AC∥DF)
小试牛刀
4.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条
件,使得能直接利用“ASA”判断△AOB≌△DOC,你补充
的条件是( )
A.OA=OD
B.OB=OC
C.AB=CD
D.OA=OC
A
小试牛刀
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
C
小试牛刀
6.如图,在△ABC中,∠B=∠C,D为BC的中点,过点D分别
向AB,AC作垂线段,则能够直接判断△BDE≌△CDF的理由
是( )
A.SSS
B.SAS
C.ASA
D.AAS
D
小试牛刀
7.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )
A.1对 B.2对
C.3对 D.4对
B
C
8.如图,将长方形纸片ABCD沿BD折叠得到△BDC′,则图中(包括实
线、虚线在内)共有全等三角形( )
A.2对 B.3对
C.4对 D.5对
小试牛刀
9.如图, BD⊥AC于点D, CE⊥AB于点E, AD=AE. 求证BE=CD.
证明:∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°.
∴△ABD≌△ACE(ASA). ∴AB=AC.
又∵AD=AE,∴AB-AE=AC-AD,即BE=CD.
在△ABD和△ACE中,
小试牛刀
10.如图,BD是平行四边形ABCD的对角线,过点A作AE⊥BD,
垂足为E,过点C作CF⊥BD,垂足为F.
(1)补全图形,并标上相应的字母;
解:如图所示.
小试牛刀
(2)求证AE=CF.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD. ∴∠ABE=∠CDF.
∴△ABE≌△CDF(AAS). ∴AE=CF.
课堂小结
课堂小结
利用两角一边判定,三角形全等
两角及其夹边
(ASA)
两角和其中一角的对边(AAS)
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
12.2
三角形全等的判定
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1. 什么是全等三角形?
2. 我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS)和边角边(SAS).
新课精讲
探索新知
1
知识点
判定两三角形全等的基本事实:角边角
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复原来三角形的原貌吗?
怎么办?可以帮帮我吗?
探索新知
画一个△A′B′C′ ,使A′B′=AB, ∠A′=∠A , ∠B′=∠B :
(1)画A ′ B′=A B;
(2)在A′B′ 的同旁画∠DA′B′=∠A, ∠EB′A′ =∠B,A′D, B′E
相交于点C′ .
A′
B′
C′
D
E
C
A
B
探索新知
归 纳
1.判定方法三:两角和它们的夹边分别相等的两个三角形全等
(简写成“角边角”或“ASA”).
2. 证明书写格式:在△ABC和△A′B′C′中,
∠A=∠A′,
AB=A′B′,
∠B=∠B′ ,
∴△ABC≌△A′B′C′.
∵
探索新知
例1 已知:如图,点D在AB上,点E在AC上,AB=AC,
∠B=∠C,求证:AD=AE.
AC=AB ,
∠C=∠B ,
∴△ACD≌△ABE(ASA).
∴AD=AE.
分析:证明△ACD≌△ABE中,就可以得出AD=AE.
∠A=∠A(公共角),
证明:在△ACD和△ABE中,
B
C
A
D
E
探索新知
总 结
在证两三角形全等所需要的角相等时,目前通常采用的方法有:
(1)公共角、对顶角分别相等;
(2)等角加(减) 等角,其和(差)相等,即等式的性质;
(3)同角或等角的余(补)角相等; (4)角平分线得到相等角;
(5)平行线的同位角、内错角相等; (6)直角都相等;
(7)全等三角形对应角相等; (8)第三角代换,即等量代换等.
典题精讲
1.如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角
形中一定和△ABC全等的图形是( )
A.甲、乙 B.甲、丙 C.乙、丙 D.乙
C
典题精讲
2.如图,某同学不小心把一块三角形玻璃打碎成三块,现在要到
玻璃店配一块与原来完全相同的玻璃,最省事的方法是( )
A.带(1)和(2)去
B.只带(2)去
C.只带(3)去
D.都带去
C
典题精讲
3.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件
后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
B
典题精讲
4.如图,AB ⊥ BC, AD ⊥ DC,垂足分别为
B,D, ∠1 = ∠2.求证AB=AD.
证明: ∵ AB⊥BC,AD⊥DC, ∴∠B=∠D=90°.
在△ABC和△ADC中,
∠B=∠D,
∠1=∠2,
AC= AC (公共边),
∴△ABC≌△ADC(AAS). ∴ AB=AD(全等三角形的对应边相等).
C
B
D
A
1
2
探索新知
2
知识点
判定两三角形全等的推论:角角边
例2 如图,AD是△ABC的中线,过C,B分别作AD及
AD的延长线的垂线CF,BE.求证:BE=CF.
导引:要证明BE=CF,可根据中线及垂线的定义和对顶角的性质来证明△BDE和△CDF全等.
探索新知
证明:∵AD是△ABC的中线,∴BD=CD.
∵CF⊥AD,BE⊥AE,∴∠CFD=∠BED=90°.
在△BDE和△CDF中,
∠BED=∠CFD,
∠BDE=∠CDF,
BD=CD,
∴△BDE≌△CDF(AAS).∴BE=CF.
探索新知
总 结
判定两三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法看缺什么条件,再去证什么条件,简言之:即综合利用分析法和综合法寻找证明途径.
典题精讲
1.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC
≌△DCB的是( )
A.∠A=∠D
B.AB=DC
C.∠ACB=∠DBC
D.AC=BD
D
典题精讲
2.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=
∠ACD=90°,且BC=CE. 求证:△ABC与△DEC全等.
证明: ∵∠BCE=∠ACD=90°, ∴∠3+∠4=∠4+∠5,
∴∠3=∠5,在△ACD中,∠ACD=90°,
∴∠2+∠D=90°,∵∠BAE=∠1+∠2=90°,
∴∠1=∠D, 在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
学以致用
小试牛刀
1.________和它们的________分别相等的两个三角形全等,可以
简写成“_________”或“______”.如图,已知
两角
夹边
角边角
ASA
∠A
∠D
2._______分别相等且其中一组_______的_______相等的两个三角
形全等,可以简写成“___________”或“________”.
两角
等角
对边
角角边
AAS
AO=DO,∠AOB与∠DOC是对顶角,
还需补充条件______=______,就可根
据“ASA”证明△AOB≌△DOC.
小试牛刀
3.如图,∠B=∠DEF,AB=DE,要判断△ABC≌△DEF,
(1)若以“ASA”为依据,还需添加的条件为
________________ ;
(2)若以“AAS”为依据,还需添加的条
件为_______________________.
∠A=∠D
∠ACB=∠F(或AC∥DF)
小试牛刀
4.如图,AC,BD相交于点O,∠A=∠D,请你再补充一个条
件,使得能直接利用“ASA”判断△AOB≌△DOC,你补充
的条件是( )
A.OA=OD
B.OB=OC
C.AB=CD
D.OA=OC
A
小试牛刀
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到
玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
C
小试牛刀
6.如图,在△ABC中,∠B=∠C,D为BC的中点,过点D分别
向AB,AC作垂线段,则能够直接判断△BDE≌△CDF的理由
是( )
A.SSS
B.SAS
C.ASA
D.AAS
D
小试牛刀
7.如图,∠1=∠2,∠3=∠4,OE=OF,则图中全等的三角形有( )
A.1对 B.2对
C.3对 D.4对
B
C
8.如图,将长方形纸片ABCD沿BD折叠得到△BDC′,则图中(包括实
线、虚线在内)共有全等三角形( )
A.2对 B.3对
C.4对 D.5对
小试牛刀
9.如图, BD⊥AC于点D, CE⊥AB于点E, AD=AE. 求证BE=CD.
证明:∵BD⊥AC于点D,CE⊥AB于点E,
∴∠ADB=∠AEC=90°.
∴△ABD≌△ACE(ASA). ∴AB=AC.
又∵AD=AE,∴AB-AE=AC-AD,即BE=CD.
在△ABD和△ACE中,
小试牛刀
10.如图,BD是平行四边形ABCD的对角线,过点A作AE⊥BD,
垂足为E,过点C作CF⊥BD,垂足为F.
(1)补全图形,并标上相应的字母;
解:如图所示.
小试牛刀
(2)求证AE=CF.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD. ∴∠ABE=∠CDF.
∴△ABE≌△CDF(AAS). ∴AE=CF.
课堂小结
课堂小结
利用两角一边判定,三角形全等
两角及其夹边
(ASA)
两角和其中一角的对边(AAS)
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
