人教版(新)八上-12.2 三角形全等的判定 第四课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-12.2 三角形全等的判定 第四课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
12.2
三角形全等的判定
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
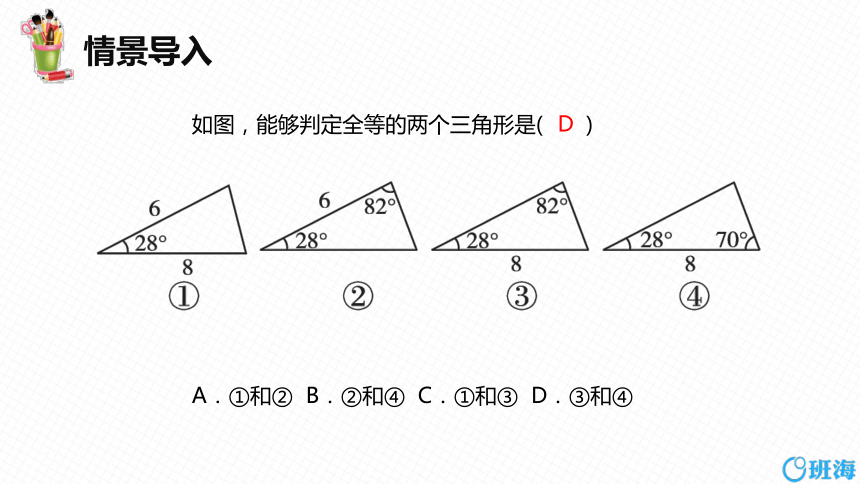
如图,能够判定全等的两个三角形是( )
A.①和② B.②和④ C.①和③ D.③和④
D
新课精讲
1
知识点
判定两直角三角形全等的方法:斜边、直角边
问题 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,
使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪
下来放到Rt△ABC上,你发现了什么?
探索新知
探索新知
A
B
C
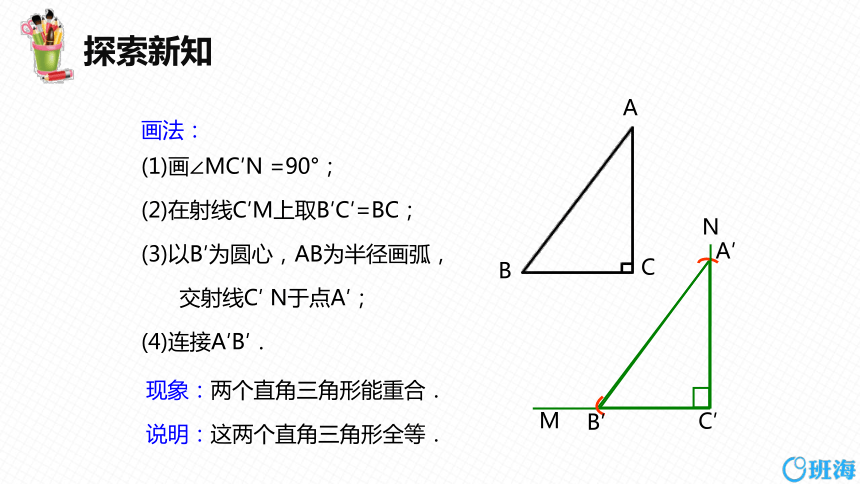
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3)以B′为圆心,AB为半径画弧,
交射线C′ N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A′
N
M
C′
B′
探索新知
由上面可以得到判定两个直角三角形全等的一
个方法:
斜边和一条直角边分别相等的两个直角三角形
全等(可以简写成“斜边、 直角边”或“HL”).
归 纳
探索新知
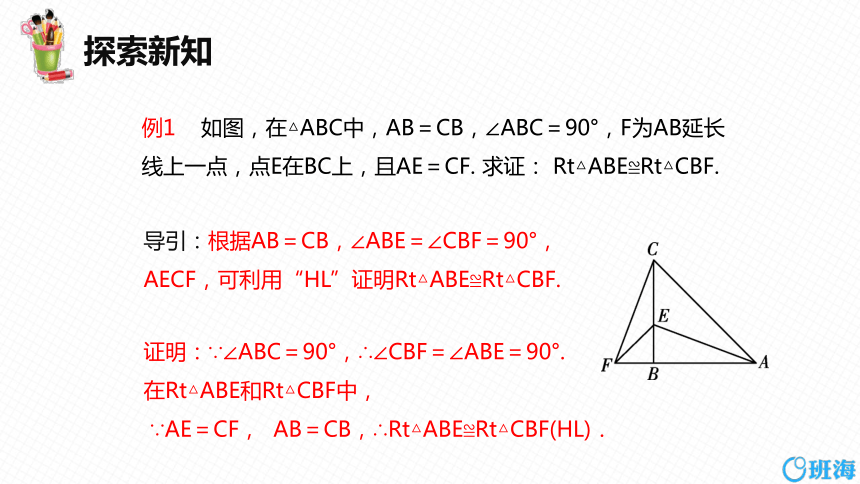
例1 如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长
线上一点,点E在BC上,且AE=CF. 求证: Rt△ABE≌Rt△CBF.
导引:根据AB=CB,∠ABE=∠CBF=90°,AECF,可利用“HL”证明Rt△ABE≌Rt△CBF.
证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF, AB=CB,∴Rt△ABE≌Rt△CBF(HL).
探索新知
总 结
应用“HL”判定两个直角三角形全等,书写时,
两个三角形符号前要加上“Rt”.
典题精讲
1.如图,点C,E,B,F在一条直线上,AB⊥CF于点B,DE⊥CF
于点E,AC=DF,AB=DE.求证:CE=BF.
证明:∵AB⊥CF,DE⊥CF, ∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.∴BC-BE=EF-BE,
即CE=BF.
典题精讲
2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt
△ABC与Rt △ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
典题精讲
3.下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
探索新知
2
知识点
直角三角形全等的综合判定
直角三角形全等的判定既可以用“SSS”“SAS”
“ASA”和“AAS”,有可以用 “HL”.
探索新知
例2 已知:如图,AC⊥BC,BD⊥AD,垂足分别为C , D, AC=BD,求证;BC=AD.
证明:∵AC⊥BC,BD⊥AD,
∴ ∠C与∠D都是直角.
在Rt△ABC≌Rt△BAD中,
AB=BA,
AC=BD,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC=AD.
D
C
A
B
典题精讲
1.下列条件可使两个直角三角形全等的是( )
A.一条边对应相等 B.两条直角边对应相等
C.一个锐角对应相等 D.两个锐角对应相等
B
2.下列条件不能使两个直角三角形全等的是( )
A.斜边和一锐角对应相等
B.有两边对应相等
C.有两个锐角对应相等
D.有一直角边和一锐角对应相等
C
典题精讲
3.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,
下面四个结论:其中正确的是__________ .(将你认为正确结论
的序号都写上)
①∠ABE= ∠BAD;
②△CEB≌△ADC;
③AB=CE;
④AD-BE=DE.
①②④
典题精讲
4.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C
在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,
则AB=________.
7
学以致用
小试牛刀
1.______和一条________分别相等的两个直角三角形全等,可以简
写成“____________________”或“____”.
斜边
直角边
斜边、直角边
HL
2.判定两三角形全等的方法有4种,分别是_____,_____,_____,
______;判定两直角三角形全等的方法有5种,分别是_______,
________,________,________,________.
SSS
SAS
ASA
AAS
HL
SSS
SAS
ASA
AAS
小试牛刀
3.如图,在△ABC中,AB=AC,若AD⊥BC,则可直接判定
△ABD和△ACD全等的方法是( )
A.SAS
B.ASA
C.SSS
D.HL
D
小试牛刀
4.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,
若AC=6 cm,则AE+DE等于( )
A.4 cm
B.5 cm
C.6 cm
D.7 cm
C
小试牛刀
5.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,
且DE=DF,连接BF,CE.下列说法:其中正确的有( )
①CE=BF; ②△ABD和△ACD的面积相等;
③BF∥CE; ④△BDF≌△CDE.
A.1个 B.2个
C.3个 D.4个
D
小试牛刀
6.如图,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件
______________________________________时,可根据“ASA”判定;
当添加条件___________时,可根据“AAS”判定;
当添加条件___________时,
可根据“SAS”判定.
∠BCA=∠DCE(或∠BCD=∠ACE)
∠A=∠E
AB=ED
小试牛刀
7.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证△ACB≌△BDA;
证明:∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形.
∴Rt△ACB≌Rt△BDA(HL).
在Rt△ACB和Rt△BDA中,
(2)若∠ABC=35°,则∠CAO=________.
20°
课堂小结
课堂小结
判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边是锐角的对边,用“AAS”判定;②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
12.2
三角形全等的判定
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,能够判定全等的两个三角形是( )
A.①和② B.②和④ C.①和③ D.③和④
D
新课精讲
1
知识点
判定两直角三角形全等的方法:斜边、直角边
问题 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,
使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪
下来放到Rt△ABC上,你发现了什么?
探索新知
探索新知
A
B
C
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C′=BC;
(3)以B′为圆心,AB为半径画弧,
交射线C′ N于点A′;
(4)连接A′B′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A′
N
M
C′
B′
探索新知
由上面可以得到判定两个直角三角形全等的一
个方法:
斜边和一条直角边分别相等的两个直角三角形
全等(可以简写成“斜边、 直角边”或“HL”).
归 纳
探索新知
例1 如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长
线上一点,点E在BC上,且AE=CF. 求证: Rt△ABE≌Rt△CBF.
导引:根据AB=CB,∠ABE=∠CBF=90°,AECF,可利用“HL”证明Rt△ABE≌Rt△CBF.
证明:∵∠ABC=90°,∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF, AB=CB,∴Rt△ABE≌Rt△CBF(HL).
探索新知
总 结
应用“HL”判定两个直角三角形全等,书写时,
两个三角形符号前要加上“Rt”.
典题精讲
1.如图,点C,E,B,F在一条直线上,AB⊥CF于点B,DE⊥CF
于点E,AC=DF,AB=DE.求证:CE=BF.
证明:∵AB⊥CF,DE⊥CF, ∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.∴BC-BE=EF-BE,
即CE=BF.
典题精讲
2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt
△ABC与Rt △ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
典题精讲
3.下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
探索新知
2
知识点
直角三角形全等的综合判定
直角三角形全等的判定既可以用“SSS”“SAS”
“ASA”和“AAS”,有可以用 “HL”.
探索新知
例2 已知:如图,AC⊥BC,BD⊥AD,垂足分别为C , D, AC=BD,求证;BC=AD.
证明:∵AC⊥BC,BD⊥AD,
∴ ∠C与∠D都是直角.
在Rt△ABC≌Rt△BAD中,
AB=BA,
AC=BD,
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC=AD.
D
C
A
B
典题精讲
1.下列条件可使两个直角三角形全等的是( )
A.一条边对应相等 B.两条直角边对应相等
C.一个锐角对应相等 D.两个锐角对应相等
B
2.下列条件不能使两个直角三角形全等的是( )
A.斜边和一锐角对应相等
B.有两边对应相等
C.有两个锐角对应相等
D.有一直角边和一锐角对应相等
C
典题精讲
3.如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于点D,
下面四个结论:其中正确的是__________ .(将你认为正确结论
的序号都写上)
①∠ABE= ∠BAD;
②△CEB≌△ADC;
③AB=CE;
④AD-BE=DE.
①②④
典题精讲
4.如图,MN∥PQ,AB⊥PQ,点A,D在直线MN上,点B,C
在直线PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,
则AB=________.
7
学以致用
小试牛刀
1.______和一条________分别相等的两个直角三角形全等,可以简
写成“____________________”或“____”.
斜边
直角边
斜边、直角边
HL
2.判定两三角形全等的方法有4种,分别是_____,_____,_____,
______;判定两直角三角形全等的方法有5种,分别是_______,
________,________,________,________.
SSS
SAS
ASA
AAS
HL
SSS
SAS
ASA
AAS
小试牛刀
3.如图,在△ABC中,AB=AC,若AD⊥BC,则可直接判定
△ABD和△ACD全等的方法是( )
A.SAS
B.ASA
C.SSS
D.HL
D
小试牛刀
4.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,
若AC=6 cm,则AE+DE等于( )
A.4 cm
B.5 cm
C.6 cm
D.7 cm
C
小试牛刀
5.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,
且DE=DF,连接BF,CE.下列说法:其中正确的有( )
①CE=BF; ②△ABD和△ACD的面积相等;
③BF∥CE; ④△BDF≌△CDE.
A.1个 B.2个
C.3个 D.4个
D
小试牛刀
6.如图,∠B=∠D,BC=DC,要判定△ABC≌△EDC,当添加条件
______________________________________时,可根据“ASA”判定;
当添加条件___________时,可根据“AAS”判定;
当添加条件___________时,
可根据“SAS”判定.
∠BCA=∠DCE(或∠BCD=∠ACE)
∠A=∠E
AB=ED
小试牛刀
7.如图,AD,BC相交于点O,AD=BC,∠C=∠D=90°.
(1)求证△ACB≌△BDA;
证明:∵∠C=∠D=90°,
∴△ACB和△BDA是直角三角形.
∴Rt△ACB≌Rt△BDA(HL).
在Rt△ACB和Rt△BDA中,
(2)若∠ABC=35°,则∠CAO=________.
20°
课堂小结
课堂小结
判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边是锐角的对边,用“AAS”判定;②直角边是锐角的邻边,用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
