人教版(新)八上-12.3 角的平分线的性质 第一课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-12.3 角的平分线的性质 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览






文档简介
(共31张PPT)
12.3 角的
平分线的性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
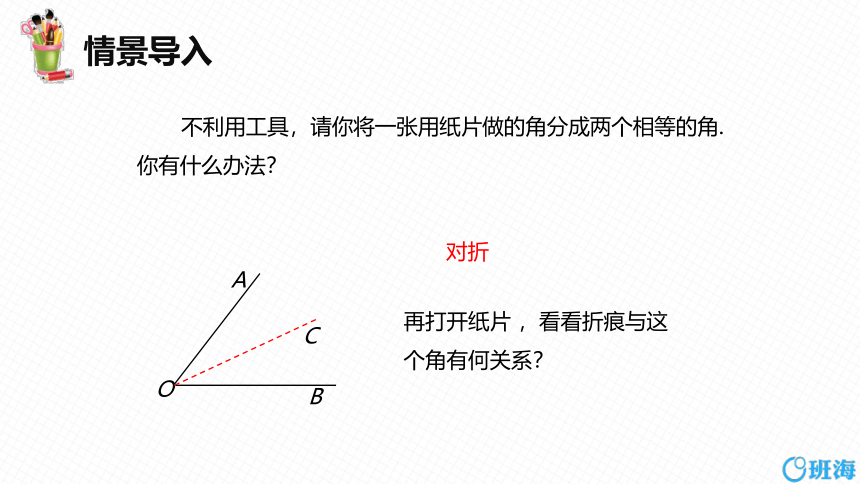
不利用工具,请你将一张用纸片做的角分成两个相等的角. 你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
新课精讲
探索新知
1
知识点
角的平分线的画法
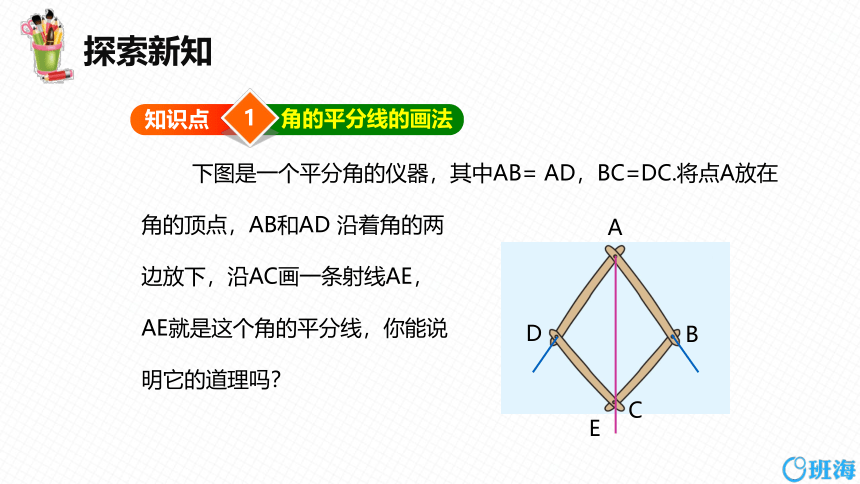
下图是一个平分角的仪器,其中AB= AD,BC=DC.将点A放在角的顶点,AB和AD 沿着角的两
边放下,沿AC画一条射线AE,
AE就是这个角的平分线,你能说
明它的道理吗?
A
B
D
C
E
探索新知
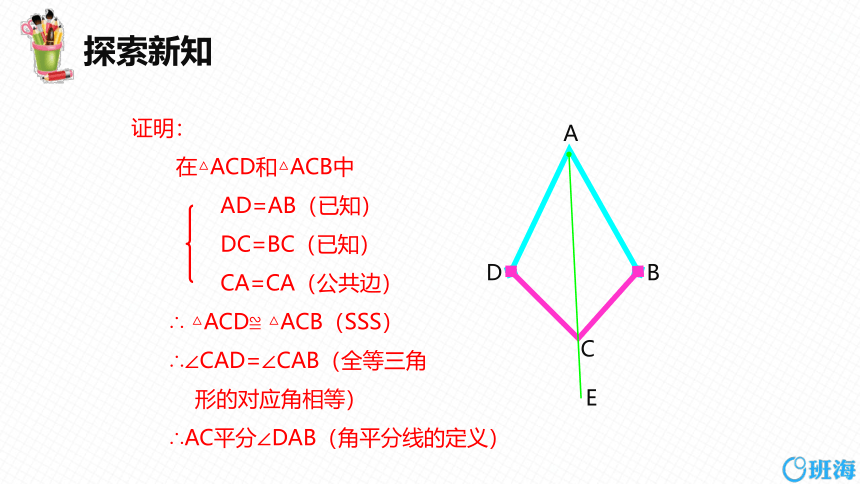
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角
形的对应角相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
探索新知
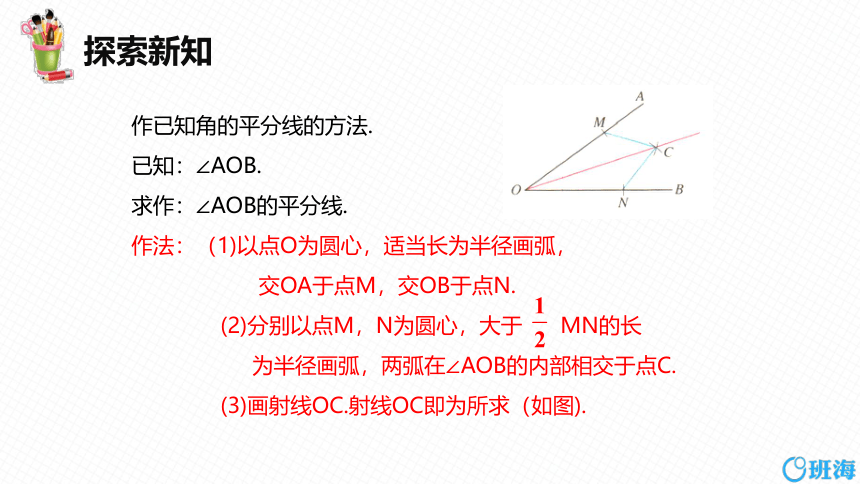
作已知角的平分线的方法.
已知:∠AOB.
求作:∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径画弧,
交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN的长
为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求(如图).
典题精讲
1.作∠AOB的平分线时,以O为圆心,某一长度为半径作弧,与
OA,OB分别相交于C,D,然后分别以C,D为圆心,适当的
长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A.大于 CD B.等于 CD
C.小于 CD D.以上答案都不对
A
典题精讲
2.如图所示,已知∠AOB,求作:∠AOM= ∠AOB.
导引:要作射线OM,使∠AOM= ∠AOB,其实质是作
∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径画弧,交OA于点E,
交OB于点F;
(2)分别以点E,F为圆心,大于 EF的长为半径画弧,
两弧在∠AOB的内部交于点C;
(3)画射线OC;
(4)同理,作∠AOC的平分线OM.∠AOM即为所求 (如上图所示).
探索新知
2
知识点
角的平分线的性质
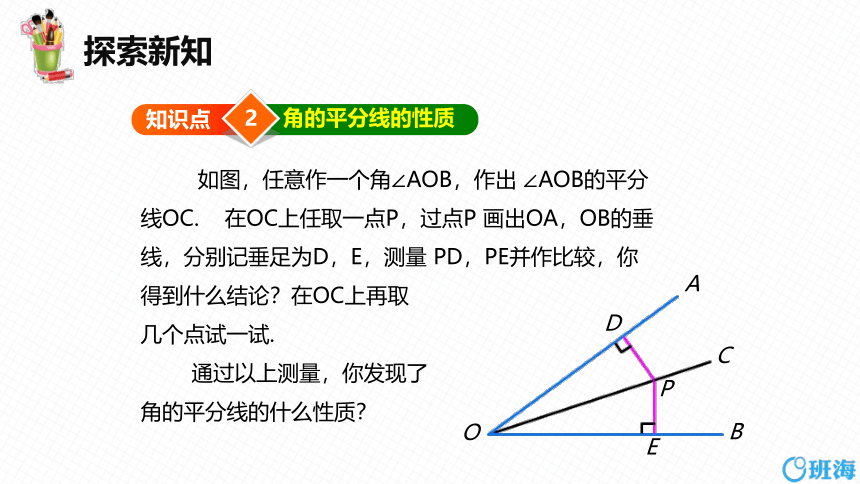
如图,任意作一个角∠AOB,作出 ∠AOB的平分
线OC. 在OC上任取一点P,过点P 画出OA,OB的垂
线,分别记垂足为D,E,测量 PD,PE并作比较,你
得到什么结论?在OC上再取
几个点试一试.
通过以上测量,你发现了
角的平分线的什么性质?
A
B
O
P
C
D
E
探索新知
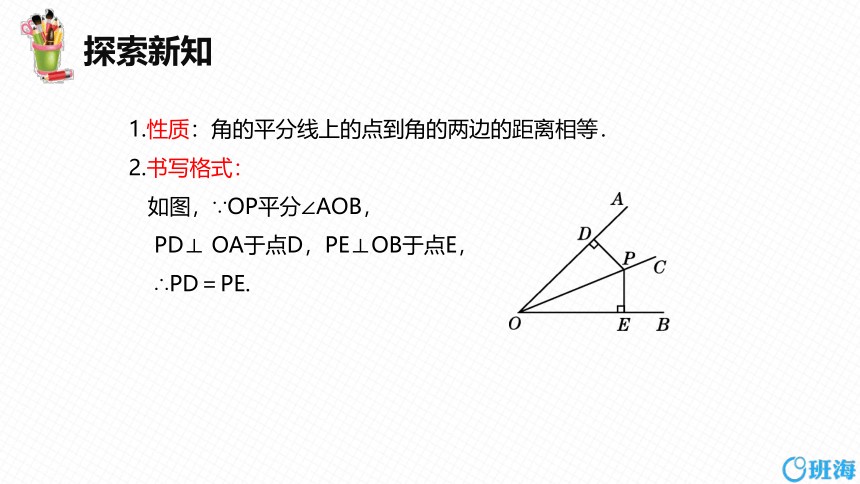
1.性质:角的平分线上的点到角的两边的距离相等.
2.书写格式:
如图,∵OP平分∠AOB,
PD⊥ OA于点D,PE⊥OB于点E,
∴PD=PE.
探索新知
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
探索新知
如图, ∠AOC=∠BOC,点 P 在OC 上,PD⊥OA,
PE⊥QB,垂足分别为D,E.求证PD=PE.
证明:∵PD⊥OA, PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∠PDO=∠PEO,
∠AOC=∠BOC,
OP=OP,
∴△PDO ≌△PEO(AAS). ∴PD=PE.
探索新知
例1 如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,F在AC上,BE=FC,求证:BD=DF.
导引:要证BD=DF,可考虑证两线段所
在的△BDE和△FDC全等,两个三角形中
已有一角和一边相等,只要再证DE=CD
即可,这可由AD平分∠CAB及垂直条件证得.
探索新知
在△BDE和△FDC中,
DE=CD ,
∠DEB=∠C,
BE=FC,
∴ △BDE ≌ △FDC ,
∴ BD=DF .
证明:∵AD平分∠CAB,DE⊥AB于E,
∠C=90°,∴DE=DC.
探索新知
总 结
由角平分线的性质不用证全等可以直接得线段相等,这是证线段相等的一个简捷方法.
典题精讲
1.如图,在直线MN上求作一点P,使点
P到射线OA和OB 的距离相等.
解:如图,过O作∠AOB的平分线,与直线MN交于点P, 点P即为所求作的点.
典题精讲
2.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交
BC于D,DE⊥AB于E,若AB=6 cm,则△DBE的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
典题精讲
3.如图,已知在△ABC中,CD是AB边上的高线, BE平分∠ABC,
交CD于点E,BC=50,DE=14,则△BCE的面积等于________.
350
学以致用
小试牛刀
1.角的平分线上的点到角的两边的距离________.用数学语
言表述为:如图,
∵∠1=∠2,且MH⊥PA,
________⊥________,
∴MH______MK.
相等
MK
PB
=
小试牛刀
2.工人师傅常用角尺平分一个任意角,做法是:如图,在∠AOB
的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相
同的刻度分别与M,N重合,得到∠AOB的平分线OP.此做法
用到三角形全等的判定方法是( )
A.SAS
B.SSS
C.ASA
D.HL
B
小试牛刀
3.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
有下列结论:
①CD=ED; ②AC+BE=AB;
③∠BDE=∠BAC; ④DA平分∠CDE.
其中结论正确的个数是( )
A.1 B.2
C.3 D.4
D
小试牛刀
4.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若
PD=2,则点P到边OA的距离是( )
A.2 B.3
C. D.4
A
5.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,
且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6
C.4 D.2
C
小试牛刀
6.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC
于点D,DE⊥AB于点E.若AB=6 cm,求△DEB的周长.
解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=ED,∠C=∠DEA=90°.
∴Rt△ACD≌Rt△AED(HL).
在Rt△ACD和Rt△AED中,
∴AC=AE. ∵CD=DE, ∴BC=CD+DB=DE+DB.
又∵AC=BC, ∴AE=AC=DE+DB.
∴DE+DB+BE=AB=6 cm. ∴△DEB的周长为6 cm.
小试牛刀
7.感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.
易知DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD
=180°,∠ABD<90°.求证DB=DC.
小试牛刀
证明:如图,过点D分别作DE⊥AB于E,DF⊥AC
交AC的延长线于F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD.
在△DEB和△DFC中,
∴△DEB≌△DFC(AAS).
∴DB=DC.
课堂小结
课堂小结
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
书写格式:
如图,∵OP平分∠AOB,
PD⊥ OA于点D,PE⊥OB于点E,
∴PD=PE.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
12.3 角的
平分线的性质
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
不利用工具,请你将一张用纸片做的角分成两个相等的角. 你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
新课精讲
探索新知
1
知识点
角的平分线的画法
下图是一个平分角的仪器,其中AB= AD,BC=DC.将点A放在角的顶点,AB和AD 沿着角的两
边放下,沿AC画一条射线AE,
AE就是这个角的平分线,你能说
明它的道理吗?
A
B
D
C
E
探索新知
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角
形的对应角相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
探索新知
作已知角的平分线的方法.
已知:∠AOB.
求作:∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径画弧,
交OA于点M,交OB于点N.
(2)分别以点M,N为圆心,大于 MN的长
为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求(如图).
典题精讲
1.作∠AOB的平分线时,以O为圆心,某一长度为半径作弧,与
OA,OB分别相交于C,D,然后分别以C,D为圆心,适当的
长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A.大于 CD B.等于 CD
C.小于 CD D.以上答案都不对
A
典题精讲
2.如图所示,已知∠AOB,求作:∠AOM= ∠AOB.
导引:要作射线OM,使∠AOM= ∠AOB,其实质是作
∠AOB的平分线.
作法:(1)以点O为圆心,适当长为半径画弧,交OA于点E,
交OB于点F;
(2)分别以点E,F为圆心,大于 EF的长为半径画弧,
两弧在∠AOB的内部交于点C;
(3)画射线OC;
(4)同理,作∠AOC的平分线OM.∠AOM即为所求 (如上图所示).
探索新知
2
知识点
角的平分线的性质
如图,任意作一个角∠AOB,作出 ∠AOB的平分
线OC. 在OC上任取一点P,过点P 画出OA,OB的垂
线,分别记垂足为D,E,测量 PD,PE并作比较,你
得到什么结论?在OC上再取
几个点试一试.
通过以上测量,你发现了
角的平分线的什么性质?
A
B
O
P
C
D
E
探索新知
1.性质:角的平分线上的点到角的两边的距离相等.
2.书写格式:
如图,∵OP平分∠AOB,
PD⊥ OA于点D,PE⊥OB于点E,
∴PD=PE.
探索新知
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
探索新知
如图, ∠AOC=∠BOC,点 P 在OC 上,PD⊥OA,
PE⊥QB,垂足分别为D,E.求证PD=PE.
证明:∵PD⊥OA, PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∠PDO=∠PEO,
∠AOC=∠BOC,
OP=OP,
∴△PDO ≌△PEO(AAS). ∴PD=PE.
探索新知
例1 如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,F在AC上,BE=FC,求证:BD=DF.
导引:要证BD=DF,可考虑证两线段所
在的△BDE和△FDC全等,两个三角形中
已有一角和一边相等,只要再证DE=CD
即可,这可由AD平分∠CAB及垂直条件证得.
探索新知
在△BDE和△FDC中,
DE=CD ,
∠DEB=∠C,
BE=FC,
∴ △BDE ≌ △FDC ,
∴ BD=DF .
证明:∵AD平分∠CAB,DE⊥AB于E,
∠C=90°,∴DE=DC.
探索新知
总 结
由角平分线的性质不用证全等可以直接得线段相等,这是证线段相等的一个简捷方法.
典题精讲
1.如图,在直线MN上求作一点P,使点
P到射线OA和OB 的距离相等.
解:如图,过O作∠AOB的平分线,与直线MN交于点P, 点P即为所求作的点.
典题精讲
2.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交
BC于D,DE⊥AB于E,若AB=6 cm,则△DBE的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
典题精讲
3.如图,已知在△ABC中,CD是AB边上的高线, BE平分∠ABC,
交CD于点E,BC=50,DE=14,则△BCE的面积等于________.
350
学以致用
小试牛刀
1.角的平分线上的点到角的两边的距离________.用数学语
言表述为:如图,
∵∠1=∠2,且MH⊥PA,
________⊥________,
∴MH______MK.
相等
MK
PB
=
小试牛刀
2.工人师傅常用角尺平分一个任意角,做法是:如图,在∠AOB
的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相
同的刻度分别与M,N重合,得到∠AOB的平分线OP.此做法
用到三角形全等的判定方法是( )
A.SAS
B.SSS
C.ASA
D.HL
B
小试牛刀
3.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
有下列结论:
①CD=ED; ②AC+BE=AB;
③∠BDE=∠BAC; ④DA平分∠CDE.
其中结论正确的个数是( )
A.1 B.2
C.3 D.4
D
小试牛刀
4.如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若
PD=2,则点P到边OA的距离是( )
A.2 B.3
C. D.4
A
5.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,
且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6
C.4 D.2
C
小试牛刀
6.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC
于点D,DE⊥AB于点E.若AB=6 cm,求△DEB的周长.
解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=ED,∠C=∠DEA=90°.
∴Rt△ACD≌Rt△AED(HL).
在Rt△ACD和Rt△AED中,
∴AC=AE. ∵CD=DE, ∴BC=CD+DB=DE+DB.
又∵AC=BC, ∴AE=AC=DE+DB.
∴DE+DB+BE=AB=6 cm. ∴△DEB的周长为6 cm.
小试牛刀
7.感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.
易知DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD
=180°,∠ABD<90°.求证DB=DC.
小试牛刀
证明:如图,过点D分别作DE⊥AB于E,DF⊥AC
交AC的延长线于F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,∴∠B=∠FCD.
在△DEB和△DFC中,
∴△DEB≌△DFC(AAS).
∴DB=DC.
课堂小结
课堂小结
角平分线的性质:
角的平分线上的点到角的两边的距离相等.
书写格式:
如图,∵OP平分∠AOB,
PD⊥ OA于点D,PE⊥OB于点E,
∴PD=PE.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
