人教版(新)八上-13.2.1 作轴对称图形【优质课件】
文档属性
| 名称 | 人教版(新)八上-13.2.1 作轴对称图形【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
13.2.1
作轴对称图形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
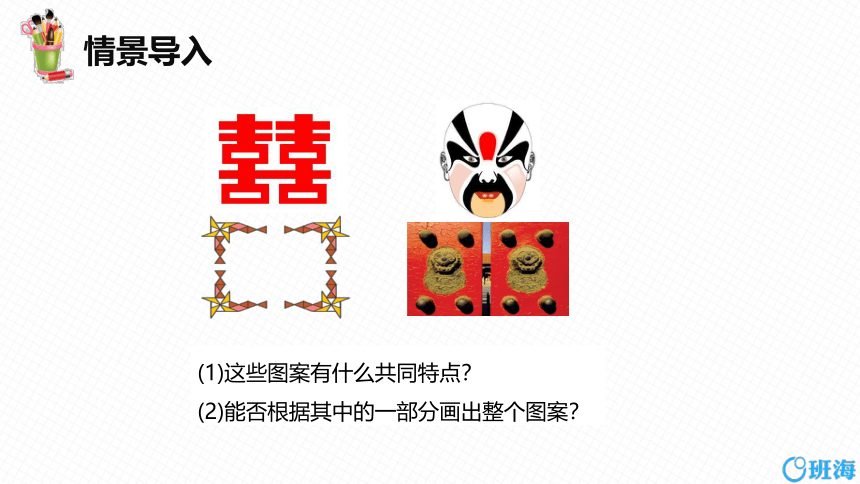
情景导入
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分画出整个图案?
新课精讲
探索新知
1
知识点
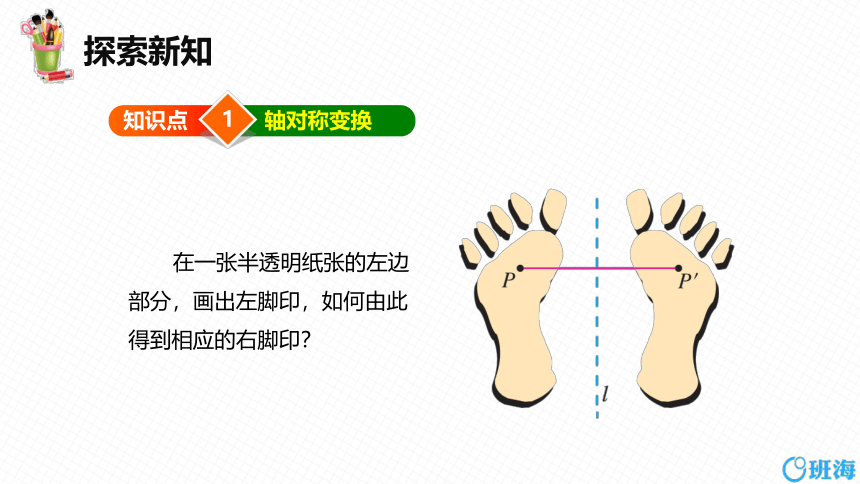
轴对称变换
在一张半透明纸张的左边部分,画出左脚印,如何由此得到相应的右脚印?
探索新知
请动手在一张纸上画一个你喜欢的图形,将这张纸纸折叠,描图,再打开纸,看看你得到了什么?
由一个平面图形得到与它关于一条直线对称的图形.
探索新知
例1 将一张长方形纸片折叠,然后用笔尖扎出“14”这个数字,将纸打开后铺平,若折痕所在直线为l,如图所示.
(1)图中的两个“14”有什么关系?
(2)在扎字的过程中,点E与点E′重合,点F与点F′重合,连接点E和点E′的线段与直线l有什么关系?连接点F与点F′时有同样的关系吗?
(3)在扎字过程中,点A与点A′重合,点B与点B′重合,线段AB与A′B′有什么关系?
(4)∠1和∠2有什么关系?
∠3与∠4有同样的关系吗?
探索新知
导引:依题意可知,两个“14”是关于直线l对称的图形,由轴对称的性质不难解决本题.
解: (1)图中的两个“14”是以直线l为对称轴的轴对称图形.
(2)EE′被直线l垂直平分,FF′也被直线l垂直平分.
(3)AB=A′B′.
(4)由于两个“14”互相重合.故有∠1=∠2,∠3=∠4.
探索新知
轴对称变换的性质:
轴对称变换前后两个图形的形状、大小一样,说明它们全等;即:变换前后的对应线段相等,对应角相等.
总 结
典题精讲
如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形 如“ ”的图形,将纸片展开,得到的图形是( )
D
探索新知
2
知识点
画轴对称图形或成轴对称
思考
如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称 的图形呢?
探索新知
1. 依据:如果一个图形关于某一条直线对称,那么连接任意一对对称点的线段被对称轴垂直平分.
2.画轴对称图形的步骤:
画轴对称图形要经历一找二作三连这三个步骤:
(1)找:在原图形上找特殊点(如线段的端点);
(2)作:作各个特殊点关于对称轴的对称点;
(3)连:按原图的顺序连接所作的各对称点.
探索新知
3.画出的新图形与原图形的关系:
(1)新图形与原图形的形状、大小完全相同;
(2)新图形上的每一点都是原图形上的某一点关于对称轴的对称点;
(3)连接任意一对对应点的线段被对称轴垂直平分.
探索新知
例2 如图,已知△ABC和直线l,画出与关于直线 l 对称的图形.
分析: △ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点 关于直线l的对称点,连接这些对称点,就能得到要画的图形.
A
B
C
l
探索新知
画法:
(1) 如图,过点A画直线l 的垂线,垂足为O,在垂线上截取OA' = OA,A'就是点A 关于直线 l 的对称点;
(2) 同理,分别画出点B,C关于直线 l 的 对称点B',C';
(3) 连接 A'B', B'C',C'A',则 △ A'B'C'即为所求.
画好后,你也可以通过折叠的方法验证一下
A
B
C
l
O
A′
B′
C′
探索新知
几何图形都可以看作由点组成 . 对于某些图形,只要画出图形中的一 些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形 的轴对称图形.
总 结
典题精讲
1.如图,把下列图形补成关于直线l对称的图形.
解:略.
2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对
折,看看哪些部 分能够重合,哪些部分不能重合.
解:略.
学以致用
小试牛刀
1.由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与
原图形的________、________完全相同;新图形上的每一点都是原图形
上的某一点关于直线l的________;连接任意一对对应点的线段被对称
轴______________.
形状
大小
对称点
垂直平分
2.下面四个图形中,把左边的图形通过轴对称变换能得到右边的图形
的是( )
D
小试牛刀
3.如图,将△ABC变换到△A′B′C′的位置,则从图中可知下列说法正确的是( )
A.△ABC与△A′B′C′是关于x轴对称的
B.△ABC与△A′B′C′是关于y轴对称的
C.△ABC与△A′B′C′不成轴对称
D.△ABC与△A′B′C′既关于x轴对称,又关于y轴对称
B
小试牛刀
4.把一张正方形纸片按图①、图
②对折两次后,再按图③挖去
一个三角形小孔,则展开后的
图形是( )
C
小试牛刀
5.在如图所示的3×3方格图中,将其中一个小方格的中心画上半径相
等的圆,使整个图形为轴对称图形,方法有( )
A.1种 B.2种
C.3种 D.4种
C
6.下面是四位同学作△ABC关于直线MN对称的△A′B′C′,其中正确的
是( )
B
小试牛刀
7.如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都
在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(2)请直接写出△AEF与四边形ABCD重叠部分的面积.
△AEF与四边形ABCD重叠部分(即图中四边形AEGD)的面积为6.
课堂小结
课堂小结
作轴对称图形的方法:
(1)确定原图形的关键点;
(2)作出每个关键点关于对称轴对称的对称点;
(3)按原图形的顺序依次连接相应的对称点.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.2.1
作轴对称图形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
(1)这些图案有什么共同特点?
(2)能否根据其中的一部分画出整个图案?
新课精讲
探索新知
1
知识点
轴对称变换
在一张半透明纸张的左边部分,画出左脚印,如何由此得到相应的右脚印?
探索新知
请动手在一张纸上画一个你喜欢的图形,将这张纸纸折叠,描图,再打开纸,看看你得到了什么?
由一个平面图形得到与它关于一条直线对称的图形.
探索新知
例1 将一张长方形纸片折叠,然后用笔尖扎出“14”这个数字,将纸打开后铺平,若折痕所在直线为l,如图所示.
(1)图中的两个“14”有什么关系?
(2)在扎字的过程中,点E与点E′重合,点F与点F′重合,连接点E和点E′的线段与直线l有什么关系?连接点F与点F′时有同样的关系吗?
(3)在扎字过程中,点A与点A′重合,点B与点B′重合,线段AB与A′B′有什么关系?
(4)∠1和∠2有什么关系?
∠3与∠4有同样的关系吗?
探索新知
导引:依题意可知,两个“14”是关于直线l对称的图形,由轴对称的性质不难解决本题.
解: (1)图中的两个“14”是以直线l为对称轴的轴对称图形.
(2)EE′被直线l垂直平分,FF′也被直线l垂直平分.
(3)AB=A′B′.
(4)由于两个“14”互相重合.故有∠1=∠2,∠3=∠4.
探索新知
轴对称变换的性质:
轴对称变换前后两个图形的形状、大小一样,说明它们全等;即:变换前后的对应线段相等,对应角相等.
总 结
典题精讲
如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形 如“ ”的图形,将纸片展开,得到的图形是( )
D
探索新知
2
知识点
画轴对称图形或成轴对称
思考
如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称 的图形呢?
探索新知
1. 依据:如果一个图形关于某一条直线对称,那么连接任意一对对称点的线段被对称轴垂直平分.
2.画轴对称图形的步骤:
画轴对称图形要经历一找二作三连这三个步骤:
(1)找:在原图形上找特殊点(如线段的端点);
(2)作:作各个特殊点关于对称轴的对称点;
(3)连:按原图的顺序连接所作的各对称点.
探索新知
3.画出的新图形与原图形的关系:
(1)新图形与原图形的形状、大小完全相同;
(2)新图形上的每一点都是原图形上的某一点关于对称轴的对称点;
(3)连接任意一对对应点的线段被对称轴垂直平分.
探索新知
例2 如图,已知△ABC和直线l,画出与关于直线 l 对称的图形.
分析: △ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点 关于直线l的对称点,连接这些对称点,就能得到要画的图形.
A
B
C
l
探索新知
画法:
(1) 如图,过点A画直线l 的垂线,垂足为O,在垂线上截取OA' = OA,A'就是点A 关于直线 l 的对称点;
(2) 同理,分别画出点B,C关于直线 l 的 对称点B',C';
(3) 连接 A'B', B'C',C'A',则 △ A'B'C'即为所求.
画好后,你也可以通过折叠的方法验证一下
A
B
C
l
O
A′
B′
C′
探索新知
几何图形都可以看作由点组成 . 对于某些图形,只要画出图形中的一 些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形 的轴对称图形.
总 结
典题精讲
1.如图,把下列图形补成关于直线l对称的图形.
解:略.
2.用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对
折,看看哪些部 分能够重合,哪些部分不能重合.
解:略.
学以致用
小试牛刀
1.由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与
原图形的________、________完全相同;新图形上的每一点都是原图形
上的某一点关于直线l的________;连接任意一对对应点的线段被对称
轴______________.
形状
大小
对称点
垂直平分
2.下面四个图形中,把左边的图形通过轴对称变换能得到右边的图形
的是( )
D
小试牛刀
3.如图,将△ABC变换到△A′B′C′的位置,则从图中可知下列说法正确的是( )
A.△ABC与△A′B′C′是关于x轴对称的
B.△ABC与△A′B′C′是关于y轴对称的
C.△ABC与△A′B′C′不成轴对称
D.△ABC与△A′B′C′既关于x轴对称,又关于y轴对称
B
小试牛刀
4.把一张正方形纸片按图①、图
②对折两次后,再按图③挖去
一个三角形小孔,则展开后的
图形是( )
C
小试牛刀
5.在如图所示的3×3方格图中,将其中一个小方格的中心画上半径相
等的圆,使整个图形为轴对称图形,方法有( )
A.1种 B.2种
C.3种 D.4种
C
6.下面是四位同学作△ABC关于直线MN对称的△A′B′C′,其中正确的
是( )
B
小试牛刀
7.如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都
在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
(1)在图中画出△AEF,使△AEF与△AEB关于直线AE对称,点F与点B是对称点;
(2)请直接写出△AEF与四边形ABCD重叠部分的面积.
△AEF与四边形ABCD重叠部分(即图中四边形AEGD)的面积为6.
课堂小结
课堂小结
作轴对称图形的方法:
(1)确定原图形的关键点;
(2)作出每个关键点关于对称轴对称的对称点;
(3)按原图形的顺序依次连接相应的对称点.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
