人教版(新)八上-13.2.2 用坐标表示轴对称【优质课件】
文档属性
| 名称 | 人教版(新)八上-13.2.2 用坐标表示轴对称【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
13.2.2
用坐标表示轴对称
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
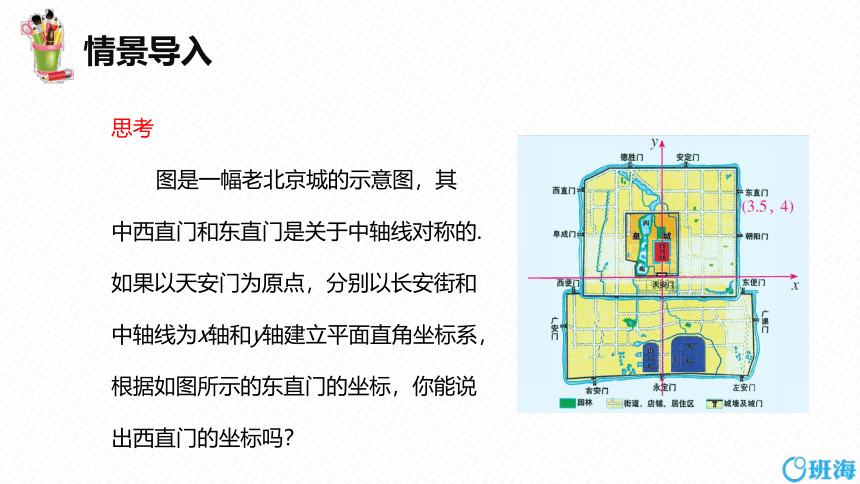
思考
图是一幅老北京城的示意图,其
中西直门和东直门是关于中轴线对称的.
如果以天安门为原点,分别以长安街和
中轴线为x轴和y轴建立平面直角坐标系,
根据如图所示的东直门的坐标,你能说
出西直门的坐标吗?
新课精讲
探索新知
1
知识点
关于x轴对称的点的坐标的特征
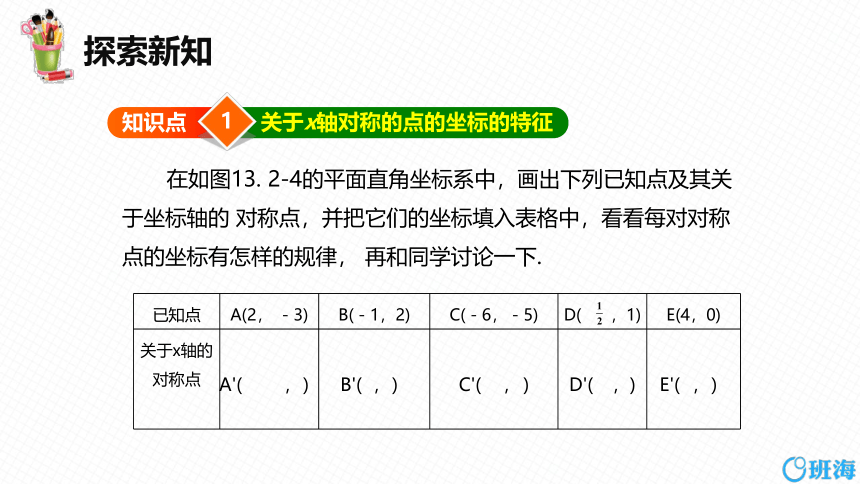
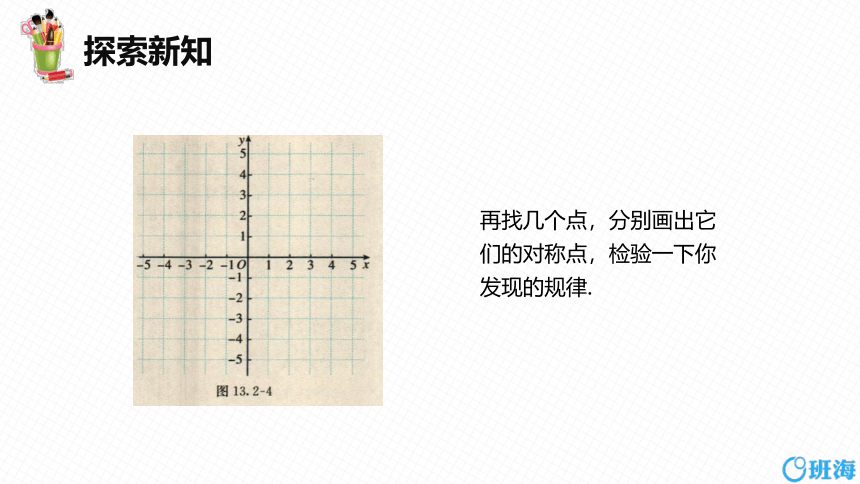
在如图13. 2-4的平面直角坐标系中,画出下列已知点及其关于坐标轴的 对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律, 再和同学讨论一下.
已知点 A(2, -3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于x轴的对称点 A'( ,) B'( ,) C'( , ) D'( ,)
E'( ,)
探索新知
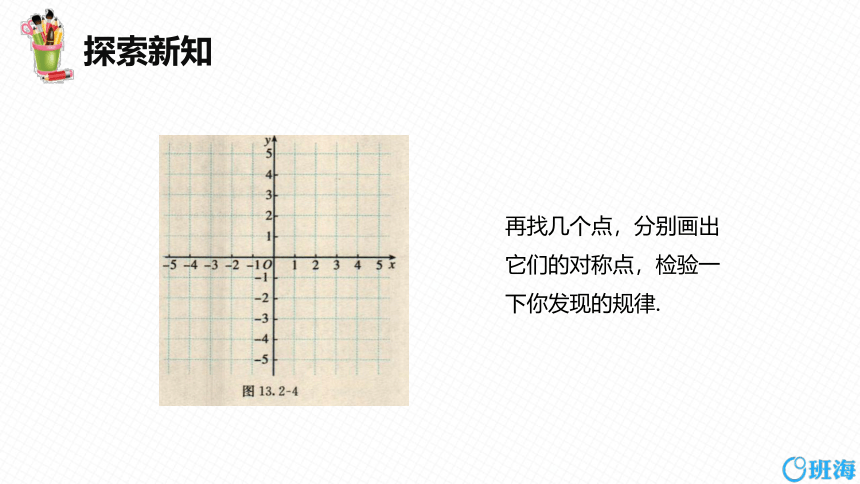
再找几个点,分别画出
它们的对称点,检验一
下你发现的规律.
探索新知
点(x , y)关于x轴对称的点的坐标为(x, -y);
其特征为:横坐标相等,纵坐标互为相反数.
归 纳
探索新知
例1 已知点P1(a-1, 5 )和P2(2, b-1)关于x轴对称,则(a+b)2016的值为( )
A. 0 B. -1 C. 1 D.(-3)2016
分析:根据关于x轴对称的点的坐标特征可知a-1=2,b -1=-5, 解方程可得a , b的值,再代入求值即可.
C
典题精讲
1.在平面直角坐标系中,点(-3,4)关于x轴对称的点是( )
A.(4,-3) B.(-3,-4)
C.(3,4) D.(3,-4)
B
2.如图,△ABO关于x轴对称,点A的坐标为 (1,-2),写出点B的坐标.
解:点B的坐标为(1, 2).
探索新知
2
知识点
关于y轴对称的点的坐标的特征
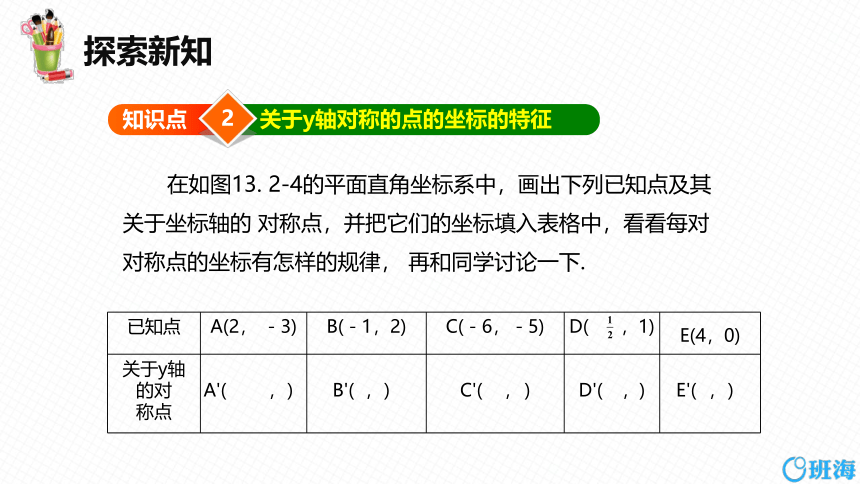
在如图13. 2-4的平面直角坐标系中,画出下列已知点及其关于坐标轴的 对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律, 再和同学讨论一下.
已知点 A(2, -3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于y轴的对 称点 A'( ,) B'( ,) C'( , ) D'( ,)
E'( ,)
探索新知
再找几个点,分别画出它们的对称点,检验一下你发现的规律.
探索新知
点(x , y)关于 y 轴对称的点的坐标为(-x, y);
其特征为:横坐标互为相反数,纵坐标相等.
总 结
探索新知
例2 如图13. 2-5,四边形ABCD的四个顶点的坐标分别为A(-5, 1), B(-2, 1),C(-2, 5), D(-5, 4),分别画出与四边形ABCD关于y轴和 x轴对称的图形.
探索新知
解:点(x , y) 关于y轴对称的点的坐标为(-x, y); 因此四边形ABCD 的顶点A,B, C, D关于y轴对称的点分别为A' ( 5,1), B' (2,1), C' (2,5), D' (5,4),依此连接A'B', B' C', C'D', D'A', 就可得到与四边形ABCD关于y轴对称的四边形A'B'C'D'.
探索新知
类似地,请你在图13. 2-5上画出与四边形ABCD关于x轴对称的图形.
对于这类问题,只要先求出已知图形 中的一些特殊点如 (多边形的顶点)的对 称点的坐标,描出并 连接这些点,就可以 得到这个图形关于坐 标轴对称的图形.
典题精讲
1.下面两点中,关于y轴对称的是( )
A.A1(-1,3),B1(1,-5)
B.A1(3,-5),B1(-3,-5)
C.A1(-2,4),B1 (2,-4)
D.A1(5,-3),B1 (5, 3)
D
典题精讲
如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),
E(2,1),则点D的坐标为( )
(-4,6)
(4,6)
(-2,1)
(6,2)
B
2.
典题精讲
3.别写出下列各点关于y轴对称的点的坐标:
(-2, 6),(1,-2),(-1, 3),(-4,-2),(1,0).
解:y轴对称的点的坐标分别为(2, 6),(-1,-2), (1, 3),(4,-2),(-1,0).
典题精讲
4.如图,利用关于坐标轴对称的点的坐标的特点,分别画出与△ABC关于x轴和y轴对称的图形.
解:图略.
学以致用
小试牛刀
1.点(x,y)关于x轴对称的点的坐标的特征是: ________相等,________
互为相反数,其坐标是_________.
横坐标
纵坐标
(x,-y)
2.点(x,y)关于y轴对称的点的坐标的特征是:
___________互为相反数,纵坐标__________,其坐标是___________.
横坐标
相等
(-x,y)
3.在平面直角坐标系中,点P(1,-2)关于x轴对称的点的坐标是( )
A.(1,2) B.(-1,-2)
C.(-1,2) D.(-2,1)
A
小试牛刀
4.点A和点B(2,-3)关于x轴对称,则A,B两点间的距离是( )
A.4 B.5 C.6 D.10
C
5.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到
点B,则点B关于x轴的对称点B′的坐标为( )
A.(-3,-2) B.(2,2)
C.(-2,2) D.(2,-2)
B
小试牛刀
6.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是
(-2,3),先把△ABC向右平移4个单位
长度得到△A1B1C1,再作与△A1B1C1关于
x轴对称的△A2B2C2,则点A的对应点A2
的坐标是( )
A.(-3,2) B.(2,-3)
C.(1,-2) D.(-1,2)
B
小试牛刀
7.在平面直角坐标系中,点A、点B关于y轴对称,点A的坐标是(2,-8),
则点B的坐标是( )
A.(-2,-8) B.(2,8)
C.(-2,8) D.(8,2)
A
8.将点A(3,2)向左平移4个单位长度得点A′,则点A′关于y轴对称的点的
坐标是( )
A.(-3,2) B.(-1,2)
C.(1,-2) D.(1,2)
D
小试牛刀
9.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一点
为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余
三个点中存在两个点关于一条坐标轴对称,则原点是( )
A.A点
B.B点
C.C点
D.D点
B
小试牛刀
10.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心
方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.
小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她
放的位置是( )
A.(-2,1)
B.(-1,1)
C.(1,-2)
D.(-1,-2)
B
小试牛刀
11.已知点M(2a-b,5+a),N(2b-1,-a+b).
(1)若点M,N关于x轴对称,试求a,b的值;
解:由题意,得
解得
(2)若点M,N关于y轴对称,试求(b+2a)2 017的值.
解:由题意,得
解得
∴(b+2a)2 017=(3-2)2 017=1.
小试牛刀
12.如图,解答下列问题:
(1)写出A,B,C三点的坐标.
(2)若△ABC各顶点的横坐标不变,
纵坐标都乘-1,请你在同一坐
标系中描出对应的点A′,B′,C′,并依次连接这三个点.所得的
△A′B′C′与△ABC有怎样的位置关系?
A(3,4),B(1,2),C(5,1).
图略;所得的△A′B′C′与△ABC关于x轴对称.
小试牛刀
13.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,
△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴正方向平移3个单位长度得到△A1B1C1,画出△A1B1C1,
并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,
并写出点C2的坐标.
图略,点B1的坐标为(-2,-1).
图略,点C2的坐标为(1,1).
课堂小结
课堂小结
两点关于x轴对称,横坐标相等,纵坐标互为相反数;
两点关于y轴对称,纵坐标相等,横坐标互为相反数;
横、纵坐标顺序不能颠倒.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.2.2
用坐标表示轴对称
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
思考
图是一幅老北京城的示意图,其
中西直门和东直门是关于中轴线对称的.
如果以天安门为原点,分别以长安街和
中轴线为x轴和y轴建立平面直角坐标系,
根据如图所示的东直门的坐标,你能说
出西直门的坐标吗?
新课精讲
探索新知
1
知识点
关于x轴对称的点的坐标的特征
在如图13. 2-4的平面直角坐标系中,画出下列已知点及其关于坐标轴的 对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律, 再和同学讨论一下.
已知点 A(2, -3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于x轴的对称点 A'( ,) B'( ,) C'( , ) D'( ,)
E'( ,)
探索新知
再找几个点,分别画出
它们的对称点,检验一
下你发现的规律.
探索新知
点(x , y)关于x轴对称的点的坐标为(x, -y);
其特征为:横坐标相等,纵坐标互为相反数.
归 纳
探索新知
例1 已知点P1(a-1, 5 )和P2(2, b-1)关于x轴对称,则(a+b)2016的值为( )
A. 0 B. -1 C. 1 D.(-3)2016
分析:根据关于x轴对称的点的坐标特征可知a-1=2,b -1=-5, 解方程可得a , b的值,再代入求值即可.
C
典题精讲
1.在平面直角坐标系中,点(-3,4)关于x轴对称的点是( )
A.(4,-3) B.(-3,-4)
C.(3,4) D.(3,-4)
B
2.如图,△ABO关于x轴对称,点A的坐标为 (1,-2),写出点B的坐标.
解:点B的坐标为(1, 2).
探索新知
2
知识点
关于y轴对称的点的坐标的特征
在如图13. 2-4的平面直角坐标系中,画出下列已知点及其关于坐标轴的 对称点,并把它们的坐标填入表格中,看看每对对称点的坐标有怎样的规律, 再和同学讨论一下.
已知点 A(2, -3) B(-1,2) C(-6,-5) D( ,1) E(4,0)
关于y轴的对 称点 A'( ,) B'( ,) C'( , ) D'( ,)
E'( ,)
探索新知
再找几个点,分别画出它们的对称点,检验一下你发现的规律.
探索新知
点(x , y)关于 y 轴对称的点的坐标为(-x, y);
其特征为:横坐标互为相反数,纵坐标相等.
总 结
探索新知
例2 如图13. 2-5,四边形ABCD的四个顶点的坐标分别为A(-5, 1), B(-2, 1),C(-2, 5), D(-5, 4),分别画出与四边形ABCD关于y轴和 x轴对称的图形.
探索新知
解:点(x , y) 关于y轴对称的点的坐标为(-x, y); 因此四边形ABCD 的顶点A,B, C, D关于y轴对称的点分别为A' ( 5,1), B' (2,1), C' (2,5), D' (5,4),依此连接A'B', B' C', C'D', D'A', 就可得到与四边形ABCD关于y轴对称的四边形A'B'C'D'.
探索新知
类似地,请你在图13. 2-5上画出与四边形ABCD关于x轴对称的图形.
对于这类问题,只要先求出已知图形 中的一些特殊点如 (多边形的顶点)的对 称点的坐标,描出并 连接这些点,就可以 得到这个图形关于坐 标轴对称的图形.
典题精讲
1.下面两点中,关于y轴对称的是( )
A.A1(-1,3),B1(1,-5)
B.A1(3,-5),B1(-3,-5)
C.A1(-2,4),B1 (2,-4)
D.A1(5,-3),B1 (5, 3)
D
典题精讲
如图,△ABC与△DEF关于y轴对称,已知A(-4,6),B(-6,2),
E(2,1),则点D的坐标为( )
(-4,6)
(4,6)
(-2,1)
(6,2)
B
2.
典题精讲
3.别写出下列各点关于y轴对称的点的坐标:
(-2, 6),(1,-2),(-1, 3),(-4,-2),(1,0).
解:y轴对称的点的坐标分别为(2, 6),(-1,-2), (1, 3),(4,-2),(-1,0).
典题精讲
4.如图,利用关于坐标轴对称的点的坐标的特点,分别画出与△ABC关于x轴和y轴对称的图形.
解:图略.
学以致用
小试牛刀
1.点(x,y)关于x轴对称的点的坐标的特征是: ________相等,________
互为相反数,其坐标是_________.
横坐标
纵坐标
(x,-y)
2.点(x,y)关于y轴对称的点的坐标的特征是:
___________互为相反数,纵坐标__________,其坐标是___________.
横坐标
相等
(-x,y)
3.在平面直角坐标系中,点P(1,-2)关于x轴对称的点的坐标是( )
A.(1,2) B.(-1,-2)
C.(-1,2) D.(-2,1)
A
小试牛刀
4.点A和点B(2,-3)关于x轴对称,则A,B两点间的距离是( )
A.4 B.5 C.6 D.10
C
5.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到
点B,则点B关于x轴的对称点B′的坐标为( )
A.(-3,-2) B.(2,2)
C.(-2,2) D.(2,-2)
B
小试牛刀
6.如图,在平面直角坐标系中,△ABC位于第二象限,点A的坐标是
(-2,3),先把△ABC向右平移4个单位
长度得到△A1B1C1,再作与△A1B1C1关于
x轴对称的△A2B2C2,则点A的对应点A2
的坐标是( )
A.(-3,2) B.(2,-3)
C.(1,-2) D.(-1,2)
B
小试牛刀
7.在平面直角坐标系中,点A、点B关于y轴对称,点A的坐标是(2,-8),
则点B的坐标是( )
A.(-2,-8) B.(2,8)
C.(-2,8) D.(8,2)
A
8.将点A(3,2)向左平移4个单位长度得点A′,则点A′关于y轴对称的点的
坐标是( )
A.(-3,2) B.(-1,2)
C.(1,-2) D.(1,2)
D
小试牛刀
9.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一点
为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余
三个点中存在两个点关于一条坐标轴对称,则原点是( )
A.A点
B.B点
C.C点
D.D点
B
小试牛刀
10.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心
方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示.
小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她
放的位置是( )
A.(-2,1)
B.(-1,1)
C.(1,-2)
D.(-1,-2)
B
小试牛刀
11.已知点M(2a-b,5+a),N(2b-1,-a+b).
(1)若点M,N关于x轴对称,试求a,b的值;
解:由题意,得
解得
(2)若点M,N关于y轴对称,试求(b+2a)2 017的值.
解:由题意,得
解得
∴(b+2a)2 017=(3-2)2 017=1.
小试牛刀
12.如图,解答下列问题:
(1)写出A,B,C三点的坐标.
(2)若△ABC各顶点的横坐标不变,
纵坐标都乘-1,请你在同一坐
标系中描出对应的点A′,B′,C′,并依次连接这三个点.所得的
△A′B′C′与△ABC有怎样的位置关系?
A(3,4),B(1,2),C(5,1).
图略;所得的△A′B′C′与△ABC关于x轴对称.
小试牛刀
13.在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,
△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴正方向平移3个单位长度得到△A1B1C1,画出△A1B1C1,
并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,
并写出点C2的坐标.
图略,点B1的坐标为(-2,-1).
图略,点C2的坐标为(1,1).
课堂小结
课堂小结
两点关于x轴对称,横坐标相等,纵坐标互为相反数;
两点关于y轴对称,纵坐标相等,横坐标互为相反数;
横、纵坐标顺序不能颠倒.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
