人教版(新)八上-13.3.1 等腰三角形 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-13.3.1 等腰三角形 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览







文档简介
(共33张PPT)
13.3.1 等腰三角形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
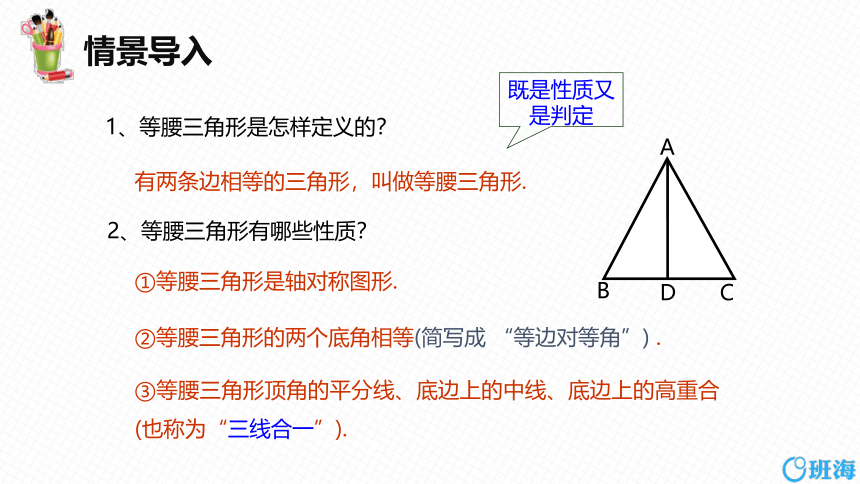
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形.
①等腰三角形是轴对称图形.
③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成 “等边对等角”) .
2、等腰三角形有哪些性质?
D
A
B
C
既是性质又是判定
新课精讲
探索新知
1
知识点
等腰三角形的判定
思考
我们知道,如果一个三角形有两条边相等,那么它们所对的角相等. 反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
探索新知
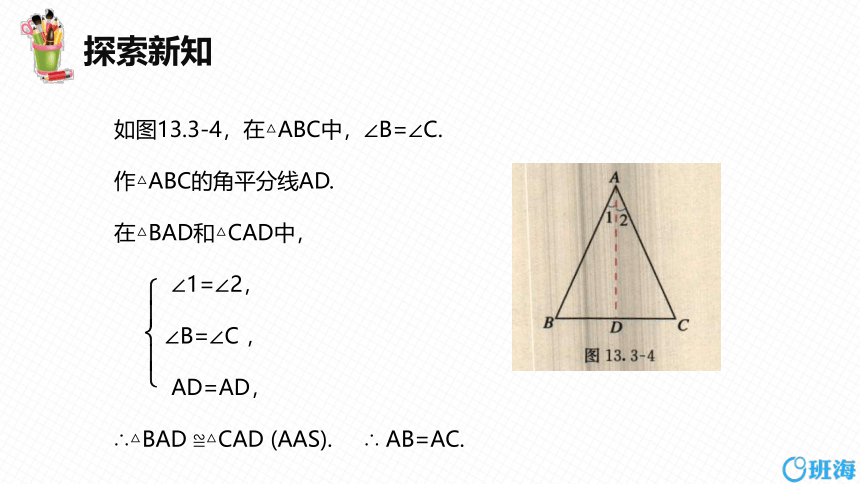
如图13.3-4,在△ABC中,∠B=∠C.
作△ABC的角平分线AD.
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C ,
AD=AD,
∴△BAD ≌△CAD (AAS). ∴ AB=AC.
探索新知
归 纳
由上面推证,我们可以得到等腰三角形的判定方法:
如果一个三角形有两个角相等.那么这两个角所对的边也相等(简写成 “等角对等边”).
探索新知
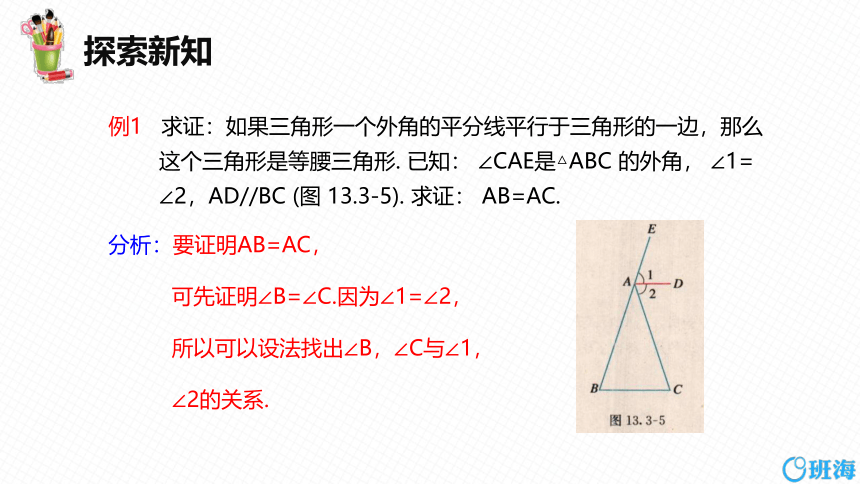
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么
这个三角形是等腰三角形. 已知: ∠CAE是△ABC 的外角, ∠1=
∠2,AD//BC (图 13.3-5). 求证: AB=AC.
分析:要证明AB=AC,
可先证明∠B=∠C.因为∠1=∠2,
所以可以设法找出∠B,∠C与∠1,
∠2的关系.
探索新知
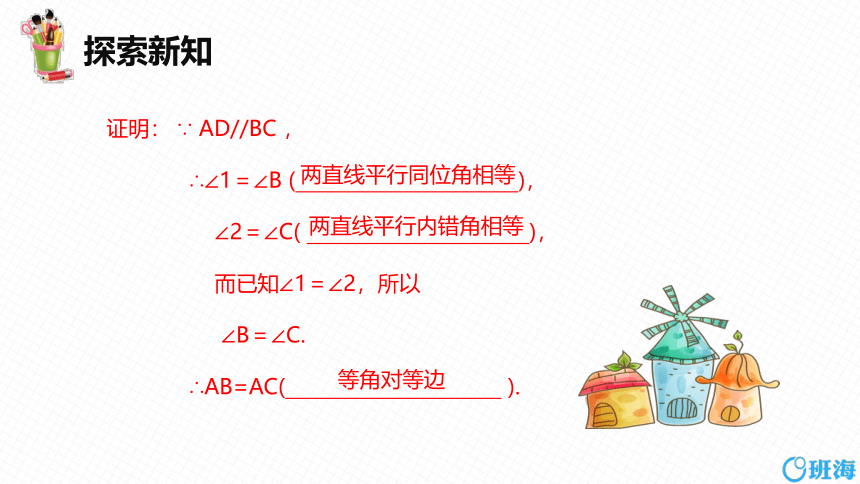
证明: ∵ AD//BC ,
∴∠1=∠B ( ),
∠2=∠C( ),
而已知∠1=∠2,所以
∠B=∠C.
∴AB=AC( ).
两直线平行同位角相等
两直线平行内错角相等
等角对等边
探索新知
总 结
等腰三角形的判定方法主要有两种:
一是判定定理;
二是定义. 另外还有很多方法,如在同一个三角形中,三线中两线重合,也能说明是等腰三角形. 但不常用,一般是通过推理得出角相等或边相等,再得出是等腰三角形.
探索新知
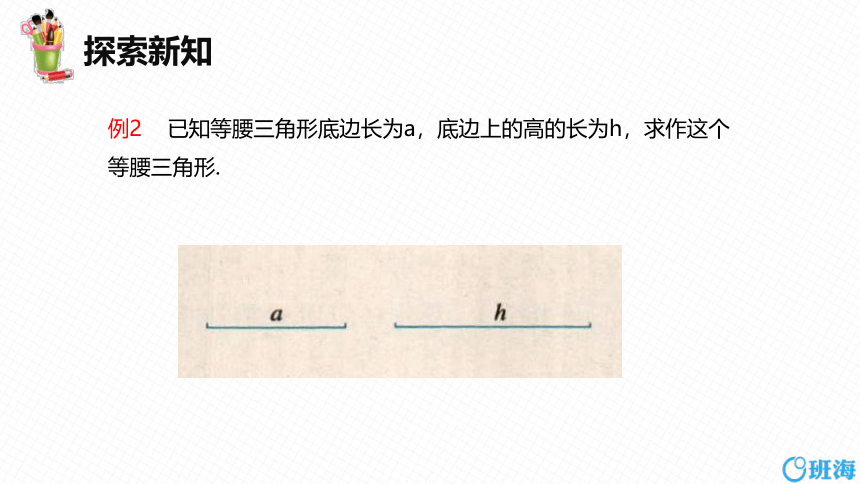
例2 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
探索新知
作法: (1)作线段AB=a.
(2)作线段AB的垂直平分线
MN,与AB相交于点D.
(3)在MN上取一点C,使DC=h.
(4)连接AC,BC,则△ABC
就是所求作的等腰三角形.
典题精讲
1.如图,∠A=36°, ∠DBC = 36°, ∠C = 72°. 分别计算∠1, ∠2的度
数,并说 明图中有哪些等腰三角形.
解: ∠1 = 72°, ∠2= 36°;
图中的等腰三角形有
△ABD,△BDC,△ABC.
典题精讲
2.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
B
3.如果一个三角形的一内角平分线垂直于对边,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
A
探索新知
2
知识点
等腰三角形的性质和判定的综合运用
等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:等边 性质判定等角.
性质
判定
探索新知
例3 如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF. 求证:DE=DF.
导引:要证DE=DF,可构造以DE和DF为对应边的全等三角形,不妨过点E作EG∥AC交BC于点G,则只要证明△EDG≌△FDC即可,缺少的条件可运用等腰三角形的性质及判定得出.
探索新知
证明:过点E作EG∥AC交BC于点G,如图,则∠1=∠F,
∠2=∠3.∵AB=AC,∴∠B=∠3(等边对等角).
∴∠B=∠2.∴BE=EG(等角对等边).
又∵BE=CF,∴EG=CF.
在△EDG和△FDC中,
∠1=∠F,
∠4=∠5,
EG= FC,
∴△EDG≌△FDC(AAS). ∴DE=DF.
典题精讲
1.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF; ②DB=DC;
③AD⊥BC; ④AC=3BF,
其中正确的结论共有 ( )
A.4个 B.3个 C.2个 D.1个
A
典题精讲
2.在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三
角形的是( )
B
学以致用
小试牛刀
1.如果一个三角形有两个角相等,那么这两个角所对的边也________(简
写成“等角对________”).
相等
等边
2.在同一个三角形中,由边________可得出它所对的________相等;反过
来,由角________也能得出它所对的边________.
相等
角
相等
相等
3.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
A.2 B.3
C.4 D.5
D
小试牛刀
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形
有( )
A.3个 B.4个
C.5个 D.6个
D
5.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,
将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直
线最多可画( )
A.3条 B.4条 C.5条 D.6条
B
小试牛刀
6. 如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正
东方向航行30 n mile到达B处后,此时测得灯塔P位于其北偏东30°方
向上,此时轮船与灯塔P的距离是( )
A.15 n mile
B.30 n mile
C.45 n mile
D.30 n mile
B
小试牛刀
7.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥
BC交AB于M,交AC于N.若BM+CN=9,则线段MN的长为( )
A.6
B.7
C.8
D.9
D
小试牛刀
8.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的
一点,过点F 作FG⊥BC于G点,并交AB于E点.
求证:(1)AD∥FG;
证明:
∵AB=AC,D是BC的中点,
∴AD⊥BC.
又∵FG⊥BC, ∴AD∥FG.
小试牛刀
(2)△AFE是等腰三角形.
∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF.
∴AF=AE,即△AEF是等腰三角形.
小试牛刀
9.如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.
(1)求证OB=OC;
证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BD,CE是△ABC的两条高线,
∴∠BDC=∠CEB=90°.
∴∠DBC=∠ECB. ∴OB=OC.
小试牛刀
(2)若∠ABC=50°,求∠BOC的度数.
解:∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°.
∴∠EOD=360°-90°-90°-80°=100°.
∴∠BOC=∠EOD=100°.
小试牛刀
10.如图,在△ABC中,AB=AC,EF交AB于点E,交AC
的延长线于点F,交BC于点D,且BE=CF.
求证DE=DF.
证明:过点E作EG∥AC交BC于点G,
∴∠F=∠DEG,∠ACB=∠EGB.
∵AB=AC,
∴∠ACB=∠B.
∴∠B=∠EGB. ∴BE=EG.
∵BE=CF,∴EG=CF.
∴△EGD≌△FCD(AAS).∴DE=DF.
在△EGD和△FCD中,
课堂小结
课堂小结
等腰三角形的三种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相等的 三角形是等腰三角形”来判定.
(2)当三角形中有两个角相等时,应用“如果一个三角形有两个角相等,那么这两个角所对的边也相等”来证明.
(3)当线段垂直平分线上的点与线段两端点构成三角形时,应用“线段垂直平分线上的点到线段两端点距离相等,则构成的三角形是等腰三角形”来证明.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.3.1 等腰三角形
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形.
①等腰三角形是轴对称图形.
③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
②等腰三角形的两个底角相等(简写成 “等边对等角”) .
2、等腰三角形有哪些性质?
D
A
B
C
既是性质又是判定
新课精讲
探索新知
1
知识点
等腰三角形的判定
思考
我们知道,如果一个三角形有两条边相等,那么它们所对的角相等. 反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系?
探索新知
如图13.3-4,在△ABC中,∠B=∠C.
作△ABC的角平分线AD.
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C ,
AD=AD,
∴△BAD ≌△CAD (AAS). ∴ AB=AC.
探索新知
归 纳
由上面推证,我们可以得到等腰三角形的判定方法:
如果一个三角形有两个角相等.那么这两个角所对的边也相等(简写成 “等角对等边”).
探索新知
例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么
这个三角形是等腰三角形. 已知: ∠CAE是△ABC 的外角, ∠1=
∠2,AD//BC (图 13.3-5). 求证: AB=AC.
分析:要证明AB=AC,
可先证明∠B=∠C.因为∠1=∠2,
所以可以设法找出∠B,∠C与∠1,
∠2的关系.
探索新知
证明: ∵ AD//BC ,
∴∠1=∠B ( ),
∠2=∠C( ),
而已知∠1=∠2,所以
∠B=∠C.
∴AB=AC( ).
两直线平行同位角相等
两直线平行内错角相等
等角对等边
探索新知
总 结
等腰三角形的判定方法主要有两种:
一是判定定理;
二是定义. 另外还有很多方法,如在同一个三角形中,三线中两线重合,也能说明是等腰三角形. 但不常用,一般是通过推理得出角相等或边相等,再得出是等腰三角形.
探索新知
例2 已知等腰三角形底边长为a,底边上的高的长为h,求作这个等腰三角形.
探索新知
作法: (1)作线段AB=a.
(2)作线段AB的垂直平分线
MN,与AB相交于点D.
(3)在MN上取一点C,使DC=h.
(4)连接AC,BC,则△ABC
就是所求作的等腰三角形.
典题精讲
1.如图,∠A=36°, ∠DBC = 36°, ∠C = 72°. 分别计算∠1, ∠2的度
数,并说 明图中有哪些等腰三角形.
解: ∠1 = 72°, ∠2= 36°;
图中的等腰三角形有
△ABD,△BDC,△ABC.
典题精讲
2.在△ABC中,∠A和∠B的度数如下,能判定△ABC是等腰三角形的是( )
A.∠A=50°,∠B=70° B.∠A=70°,∠B=40°
C.∠A=30°,∠B=90° D.∠A=80°,∠B=60°
B
3.如果一个三角形的一内角平分线垂直于对边,那么这个三角形一定是( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
A
探索新知
2
知识点
等腰三角形的性质和判定的综合运用
等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:等边 性质判定等角.
性质
判定
探索新知
例3 如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF. 求证:DE=DF.
导引:要证DE=DF,可构造以DE和DF为对应边的全等三角形,不妨过点E作EG∥AC交BC于点G,则只要证明△EDG≌△FDC即可,缺少的条件可运用等腰三角形的性质及判定得出.
探索新知
证明:过点E作EG∥AC交BC于点G,如图,则∠1=∠F,
∠2=∠3.∵AB=AC,∴∠B=∠3(等边对等角).
∴∠B=∠2.∴BE=EG(等角对等边).
又∵BE=CF,∴EG=CF.
在△EDG和△FDC中,
∠1=∠F,
∠4=∠5,
EG= FC,
∴△EDG≌△FDC(AAS). ∴DE=DF.
典题精讲
1.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF; ②DB=DC;
③AD⊥BC; ④AC=3BF,
其中正确的结论共有 ( )
A.4个 B.3个 C.2个 D.1个
A
典题精讲
2.在下列三角形中,若AB=AC,则不能被一条直线分成两个小等腰三
角形的是( )
B
学以致用
小试牛刀
1.如果一个三角形有两个角相等,那么这两个角所对的边也________(简
写成“等角对________”).
相等
等边
2.在同一个三角形中,由边________可得出它所对的________相等;反过
来,由角________也能得出它所对的边________.
相等
角
相等
相等
3.如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
A.2 B.3
C.4 D.5
D
小试牛刀
4.如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形
有( )
A.3个 B.4个
C.5个 D.6个
D
5.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,
将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直
线最多可画( )
A.3条 B.4条 C.5条 D.6条
B
小试牛刀
6. 如图,一艘轮船在A处测得灯塔P位于其北偏东60°方向上,轮船沿正
东方向航行30 n mile到达B处后,此时测得灯塔P位于其北偏东30°方
向上,此时轮船与灯塔P的距离是( )
A.15 n mile
B.30 n mile
C.45 n mile
D.30 n mile
B
小试牛刀
7.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥
BC交AB于M,交AC于N.若BM+CN=9,则线段MN的长为( )
A.6
B.7
C.8
D.9
D
小试牛刀
8.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的
一点,过点F 作FG⊥BC于G点,并交AB于E点.
求证:(1)AD∥FG;
证明:
∵AB=AC,D是BC的中点,
∴AD⊥BC.
又∵FG⊥BC, ∴AD∥FG.
小试牛刀
(2)△AFE是等腰三角形.
∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF.
∴AF=AE,即△AEF是等腰三角形.
小试牛刀
9.如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O.
(1)求证OB=OC;
证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BD,CE是△ABC的两条高线,
∴∠BDC=∠CEB=90°.
∴∠DBC=∠ECB. ∴OB=OC.
小试牛刀
(2)若∠ABC=50°,求∠BOC的度数.
解:∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°.
∴∠EOD=360°-90°-90°-80°=100°.
∴∠BOC=∠EOD=100°.
小试牛刀
10.如图,在△ABC中,AB=AC,EF交AB于点E,交AC
的延长线于点F,交BC于点D,且BE=CF.
求证DE=DF.
证明:过点E作EG∥AC交BC于点G,
∴∠F=∠DEG,∠ACB=∠EGB.
∵AB=AC,
∴∠ACB=∠B.
∴∠B=∠EGB. ∴BE=EG.
∵BE=CF,∴EG=CF.
∴△EGD≌△FCD(AAS).∴DE=DF.
在△EGD和△FCD中,
课堂小结
课堂小结
等腰三角形的三种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相等的 三角形是等腰三角形”来判定.
(2)当三角形中有两个角相等时,应用“如果一个三角形有两个角相等,那么这两个角所对的边也相等”来证明.
(3)当线段垂直平分线上的点与线段两端点构成三角形时,应用“线段垂直平分线上的点到线段两端点距离相等,则构成的三角形是等腰三角形”来证明.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
