人教版(新)八上-13.3.2 等边三角形 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-13.3.2 等边三角形 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览









文档简介
(共31张PPT)
13.3.2 等边三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
思考1 等边三角形是轴对称图形,若沿着其中一条对称轴折叠,能产生什么特殊图形?
思考2 这个特殊的直角三角形相比一般的直角三角形有什么不同之处,它有什么特殊性质?
新课精讲
探索新知
1
知识点
含30°角的直角三角形的性质
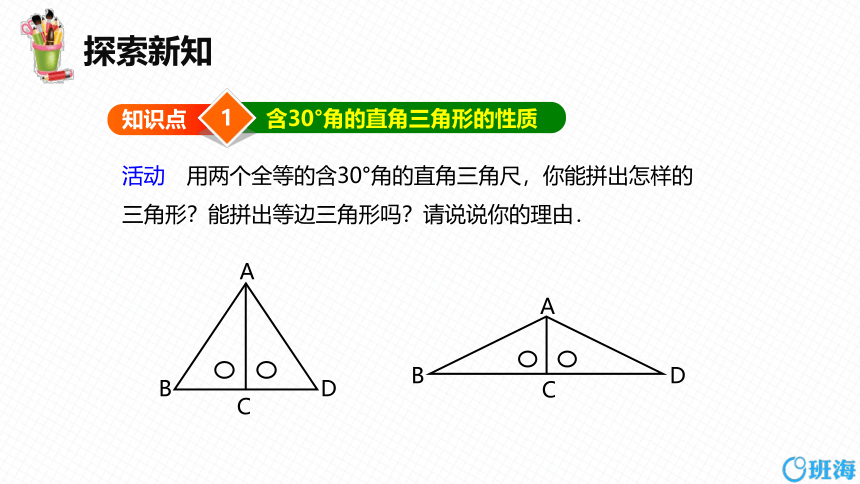
活动 用两个全等的含30°角的直角三角尺,你能拼出怎样的三角形?能拼出等边三角形吗?请说说你的理由.
A
B
D
C
A
B
C
D
探索新知
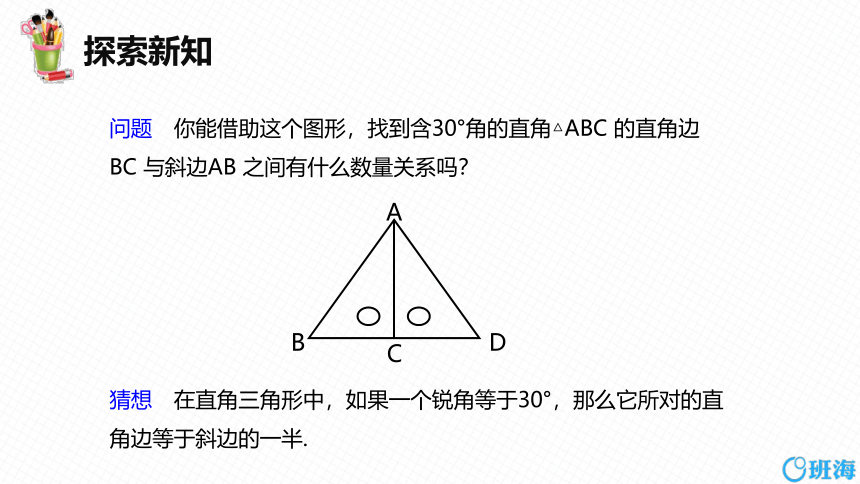
问题 你能借助这个图形,找到含30°角的直角△ABC 的直角边BC 与斜边AB 之间有什么数量关系吗?
A
B
D
C
猜想 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
探索新知
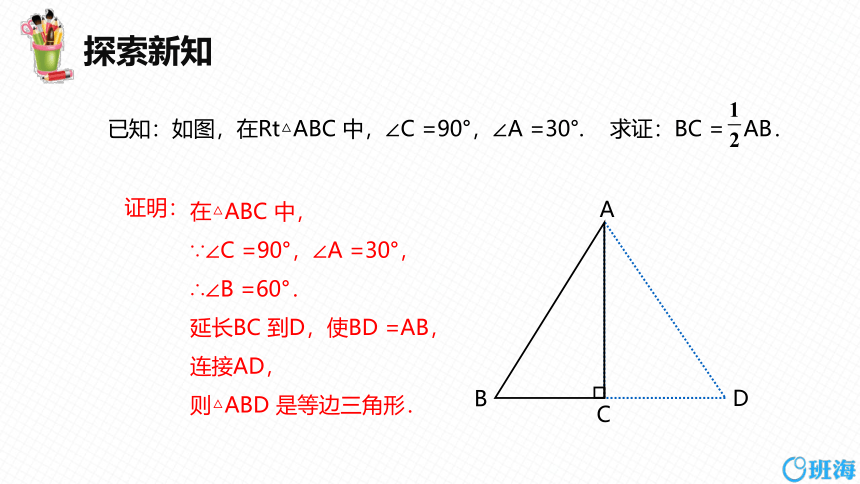
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB.
在△ABC 中,
∵∠C =90°,∠A =30°,
∴∠B =60°.
延长BC 到D,使BD =AB,
连接AD,
则△ABD 是等边三角形.
A
B
C
D
证明:
探索新知
等边三角形的性质可知,AC也是BD 边上的中线,
∴BC = BD = AB
在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.
定理:
探索新知
例1 图13. 3-9是屋架设计图的一部分,点 D是斜梁AB的中点,立柱BC,DE垂直于横梁AC, AB = 7.4m,∠A = 30°立柱 BC, DE 要多长.
解: ∵DE⊥AC,BC⊥AC,∠A=30°,
∴BC= AB , DE = AD.
∴BC= ×7.4=3.7(m).
又AD= AB,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m , DE的长是1.85m.
探索新知
总 结
利用含30°角的直角三角形的性质,关键有两个元素:
一是30°的角;二是直角三角形.根据这两个元素可建立直角三角形中斜边与直角边之间的关系.
典题精讲
1.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,
则AB等于( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
C
典题精讲
2.如图,已知在△ABC中,AB=AC,∠C=30°,AB⊥AD,则下列关
系式正确的为( )
A.BD=CD
B.BD=2CD
C.BD=3CD
D.BD=4CD
B
探索新知
2
知识点
含30°角的直角三角形性质的应用
例2 如图,某货轮于上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到达C,D处的时间.
导引:说明△ABC是等腰三角形及△BCD是等边
三角形是解决本题的关键.
探索新知
解:由已知,得∠BAC=90°-60°=30°,
∠ACB=90°+30°=120°,∠BCD=∠BDC=60°,
∴∠ABC=∠BCD-∠BAC=30°, ∠CBD=180°-∠BCD-∠BDC=60°,
∴∠ABC=∠BAC=30°, ∴AC=BC=60 海里,
∴货轮从A处到C处所需时间为60÷30=2(小时).
∵∠CBD=∠BCD=∠BDC =60°,
∴△BCD是等边三角形, ∴CD=BC=60海里,
∴货轮从C处到D处所需时间为60÷30=2(小时),
∴货轮 从A处到D处所需时间为2+2=4(小时).
答:该货轮到达C处的时间是上午10时20分,到达D处的时间是中午12时20分.
探索新知
总 结
本题运用建模思想,把实际问题转化为等边三角形和等腰三角形模型,从而利用等边三角形、等腰三角形及方位角的有关知识解决问题.
典题精讲
1.如图是屋架设计图的一部分,立柱BC垂直于 横梁AD,AB=8 m,
∠A=30°,则立柱BC的长度为( )
A.4 m
B.8 m
C.10
D.16 m
A
典题精讲
2.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别
表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则
乘电梯从点B到点C上升的高度h是( )
A.3 m
B.4 m
C.5 m
D.6 m
B
学以致用
小试牛刀
1.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于
____________________.
斜边的一半
2.如图,在Rt△ABE中,∠A=90°,∠B=60°,
BE=10,D是线段AE上的一动点,过点D作
CD交BE于点C,并使得∠CDE=30°,则CD
长度的取值范围是______________.
0<CD≤5
小试牛刀
3.实际中有关测量的应用,常常要涉及建立直角三角形模型问题,用
________三角形的性质解决实际问题.
直角
4.如图,某轮船于上午11时30分在A处观测海岛B在北偏东60°方向,该
轮船以每小时10 n mile的速度向东航行到C处,在C处观测到海岛B在
北偏东30°方向,继续向东航行到D处,在
D处观测到海岛B在北偏西30°方向,当轮船
到达C处时恰与海岛B相距20 n mile.则轮船
到达C处的时间为__________________,
到达D处的时间为__________________.
13时30分
15时30分
小试牛刀
5.已知在Rt△ABC中,CD是斜边AB上的高,∠B=30°,CD=2 cm,
则BC的长是( )
A.2 cm B.4 cm
C.8 cm D.16 cm
B
6.△ABC中,∠A:∠B:∠C=1:2:3,则BC:AB等于( )
A.2:1 B.1:2
C.1:3 D.2:3
B
小试牛刀
7.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥
AC于点E.若AE=2,则EC的长为( )
A.2 B.4
C.6 D.8
C
8.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC
于点E,垂足为点D.若BE=6 cm,则AC等于( )
A.6 cm B.5 cm
C.4 cm D.3 cm
D
小试牛刀
9.小明用测角仪器量出上山的路的坡角(斜坡与水平面的夹角)为30°,他又
测得上山沿坡路登上山顶共需走2 000 m,于是他知道这座山高( )
A.500 m B.1 000 m
C.1 200 m D.1 500 m
B
10.如图,一棵大树在一次强台风中离地面5 m处折断倒下,倒下部分
与地面成30°角,这棵大树在折断前的高度为( )
A.10 m B.15 m
C.25 m D.30 m
B
小试牛刀
11.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥
AB,DF⊥AC,垂足分别为E,F.
(1)求证DE=DF;
证明:∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°. ∵AB=AC,∴∠B=∠C.
∵D是BC的中点, ∴BD=CD.
在△BED和△CFD中,
∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFD(AAS). ∴DE=DF.
小试牛刀
(2)若∠A=60°,BE=1,求△ABC的周长.
解:∵AB=AC,∠A=60°,
∴△ABC为等边三角形.∴∠B=60°.
∵∠BED=90°,∴∠BDE=30°.
∴BE= BD.
∵BE=1,∴BD=2.∴BC=2BD=4.
∴△ABC的周长为12.
小试牛刀
12.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC
于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
解:由题意知AB=BC=AC=8,∠B=∠A=∠C=60°.
∴BD=AB-AD=8-2=6,∠BDE=90°-60°=30°,
∴BE= BD=3. EC=8-3=5.
∵∠FEC=90°-60°=30°,
∴FC=5× = . ∴AF=8- = .
小试牛刀
(2)当AD取何值时,DE=EF
当DE=EF时,易证△BDE≌△CEF,
∴BE=CF,BD=CE.
∵CF= CE,∴BE= CE.
又∵BE+CE=8,
∴CE= .∴BD= .∴AD= .即当AD= 时,DE=EF.
课堂小结
课堂小结
定理 在直角三角形中,30°角所对的直角边等于斜边的一半.
利用含30°角的直角三角形的性质求有关线段的长:
依据:直角三角形中30°角所对的直角边等于斜边的一半.
用途:求线段长度和证明线段倍分关系.
作法:当图形中含有30°角时,通过作垂线构造含有30°角的直角三角形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.3.2 等边三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
思考1 等边三角形是轴对称图形,若沿着其中一条对称轴折叠,能产生什么特殊图形?
思考2 这个特殊的直角三角形相比一般的直角三角形有什么不同之处,它有什么特殊性质?
新课精讲
探索新知
1
知识点
含30°角的直角三角形的性质
活动 用两个全等的含30°角的直角三角尺,你能拼出怎样的三角形?能拼出等边三角形吗?请说说你的理由.
A
B
D
C
A
B
C
D
探索新知
问题 你能借助这个图形,找到含30°角的直角△ABC 的直角边BC 与斜边AB 之间有什么数量关系吗?
A
B
D
C
猜想 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
探索新知
已知:如图,在Rt△ABC 中,∠C =90°,∠A =30°. 求证:BC = AB.
在△ABC 中,
∵∠C =90°,∠A =30°,
∴∠B =60°.
延长BC 到D,使BD =AB,
连接AD,
则△ABD 是等边三角形.
A
B
C
D
证明:
探索新知
等边三角形的性质可知,AC也是BD 边上的中线,
∴BC = BD = AB
在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半.
定理:
探索新知
例1 图13. 3-9是屋架设计图的一部分,点 D是斜梁AB的中点,立柱BC,DE垂直于横梁AC, AB = 7.4m,∠A = 30°立柱 BC, DE 要多长.
解: ∵DE⊥AC,BC⊥AC,∠A=30°,
∴BC= AB , DE = AD.
∴BC= ×7.4=3.7(m).
又AD= AB,
∴DE= AD= ×3.7=1.85(m).
答:立柱BC的长是3.7m , DE的长是1.85m.
探索新知
总 结
利用含30°角的直角三角形的性质,关键有两个元素:
一是30°的角;二是直角三角形.根据这两个元素可建立直角三角形中斜边与直角边之间的关系.
典题精讲
1.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=12 cm,
则AB等于( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
C
典题精讲
2.如图,已知在△ABC中,AB=AC,∠C=30°,AB⊥AD,则下列关
系式正确的为( )
A.BD=CD
B.BD=2CD
C.BD=3CD
D.BD=4CD
B
探索新知
2
知识点
含30°角的直角三角形性质的应用
例2 如图,某货轮于上午8时20分从A处出发,此时观测到海岛B的方位为北偏东60°,该货轮以每小时30海里的速度向东航行到C处,此时观测到海岛B的方位为北偏东30°,继续向东航行到D处,观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里,求该货轮到达C,D处的时间.
导引:说明△ABC是等腰三角形及△BCD是等边
三角形是解决本题的关键.
探索新知
解:由已知,得∠BAC=90°-60°=30°,
∠ACB=90°+30°=120°,∠BCD=∠BDC=60°,
∴∠ABC=∠BCD-∠BAC=30°, ∠CBD=180°-∠BCD-∠BDC=60°,
∴∠ABC=∠BAC=30°, ∴AC=BC=60 海里,
∴货轮从A处到C处所需时间为60÷30=2(小时).
∵∠CBD=∠BCD=∠BDC =60°,
∴△BCD是等边三角形, ∴CD=BC=60海里,
∴货轮从C处到D处所需时间为60÷30=2(小时),
∴货轮 从A处到D处所需时间为2+2=4(小时).
答:该货轮到达C处的时间是上午10时20分,到达D处的时间是中午12时20分.
探索新知
总 结
本题运用建模思想,把实际问题转化为等边三角形和等腰三角形模型,从而利用等边三角形、等腰三角形及方位角的有关知识解决问题.
典题精讲
1.如图是屋架设计图的一部分,立柱BC垂直于 横梁AD,AB=8 m,
∠A=30°,则立柱BC的长度为( )
A.4 m
B.8 m
C.10
D.16 m
A
典题精讲
2.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别
表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则
乘电梯从点B到点C上升的高度h是( )
A.3 m
B.4 m
C.5 m
D.6 m
B
学以致用
小试牛刀
1.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于
____________________.
斜边的一半
2.如图,在Rt△ABE中,∠A=90°,∠B=60°,
BE=10,D是线段AE上的一动点,过点D作
CD交BE于点C,并使得∠CDE=30°,则CD
长度的取值范围是______________.
0<CD≤5
小试牛刀
3.实际中有关测量的应用,常常要涉及建立直角三角形模型问题,用
________三角形的性质解决实际问题.
直角
4.如图,某轮船于上午11时30分在A处观测海岛B在北偏东60°方向,该
轮船以每小时10 n mile的速度向东航行到C处,在C处观测到海岛B在
北偏东30°方向,继续向东航行到D处,在
D处观测到海岛B在北偏西30°方向,当轮船
到达C处时恰与海岛B相距20 n mile.则轮船
到达C处的时间为__________________,
到达D处的时间为__________________.
13时30分
15时30分
小试牛刀
5.已知在Rt△ABC中,CD是斜边AB上的高,∠B=30°,CD=2 cm,
则BC的长是( )
A.2 cm B.4 cm
C.8 cm D.16 cm
B
6.△ABC中,∠A:∠B:∠C=1:2:3,则BC:AB等于( )
A.2:1 B.1:2
C.1:3 D.2:3
B
小试牛刀
7.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥
AC于点E.若AE=2,则EC的长为( )
A.2 B.4
C.6 D.8
C
8.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC
于点E,垂足为点D.若BE=6 cm,则AC等于( )
A.6 cm B.5 cm
C.4 cm D.3 cm
D
小试牛刀
9.小明用测角仪器量出上山的路的坡角(斜坡与水平面的夹角)为30°,他又
测得上山沿坡路登上山顶共需走2 000 m,于是他知道这座山高( )
A.500 m B.1 000 m
C.1 200 m D.1 500 m
B
10.如图,一棵大树在一次强台风中离地面5 m处折断倒下,倒下部分
与地面成30°角,这棵大树在折断前的高度为( )
A.10 m B.15 m
C.25 m D.30 m
B
小试牛刀
11.如图,已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥
AB,DF⊥AC,垂足分别为E,F.
(1)求证DE=DF;
证明:∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°. ∵AB=AC,∴∠B=∠C.
∵D是BC的中点, ∴BD=CD.
在△BED和△CFD中,
∠BED=∠CFD,∠B=∠C,BD=CD,
∴△BED≌△CFD(AAS). ∴DE=DF.
小试牛刀
(2)若∠A=60°,BE=1,求△ABC的周长.
解:∵AB=AC,∠A=60°,
∴△ABC为等边三角形.∴∠B=60°.
∵∠BED=90°,∴∠BDE=30°.
∴BE= BD.
∵BE=1,∴BD=2.∴BC=2BD=4.
∴△ABC的周长为12.
小试牛刀
12.如图,等边△ABC的边长为8,D为AB边上一动点,过点D作DE⊥BC
于点E,过点E作EF⊥AC于点F.
(1)若AD=2,求AF的长;
解:由题意知AB=BC=AC=8,∠B=∠A=∠C=60°.
∴BD=AB-AD=8-2=6,∠BDE=90°-60°=30°,
∴BE= BD=3. EC=8-3=5.
∵∠FEC=90°-60°=30°,
∴FC=5× = . ∴AF=8- = .
小试牛刀
(2)当AD取何值时,DE=EF
当DE=EF时,易证△BDE≌△CEF,
∴BE=CF,BD=CE.
∵CF= CE,∴BE= CE.
又∵BE+CE=8,
∴CE= .∴BD= .∴AD= .即当AD= 时,DE=EF.
课堂小结
课堂小结
定理 在直角三角形中,30°角所对的直角边等于斜边的一半.
利用含30°角的直角三角形的性质求有关线段的长:
依据:直角三角形中30°角所对的直角边等于斜边的一半.
用途:求线段长度和证明线段倍分关系.
作法:当图形中含有30°角时,通过作垂线构造含有30°角的直角三角形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
