人教版(新)四上 第六单元 6.商的变化规律【优质课件】
文档属性
| 名称 | 人教版(新)四上 第六单元 6.商的变化规律【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览







文档简介
(共22张PPT)
商的变化规律
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
课前导入
学以致用
新课精讲
课堂小结
01
02
03
04
目 录
课前导入
01
情景导入
花果山风景秀丽,气候宜人,那里住着一群猴子。有一天,猴王让一只小猴分桃子。猴王说:“给你4个桃子,平均分给2只猴吧。”小猴听了,连连摇头说:“太少了,太少了。”猴王又说:“好吧,给你40个桃子,平均分给20只猴,怎么样?”小猴得寸进尺,挠挠头皮,试探地说:“大王,再多给点行不行啊?”猴王一拍桌子,显示出慷慨大度的样子说:“那好吧,给你400个桃子,平均分给200只小猴,你总该满意了吧?” 小猴子连忙说:“好了、好了”!猴王听了哈哈大笑。
猴王分桃的故事
你知道猴王为什么笑吗?
新课精讲
02
探索新知
你能把两个发现合并成一句话吗?
先观察第(1)组,你能发现什么?
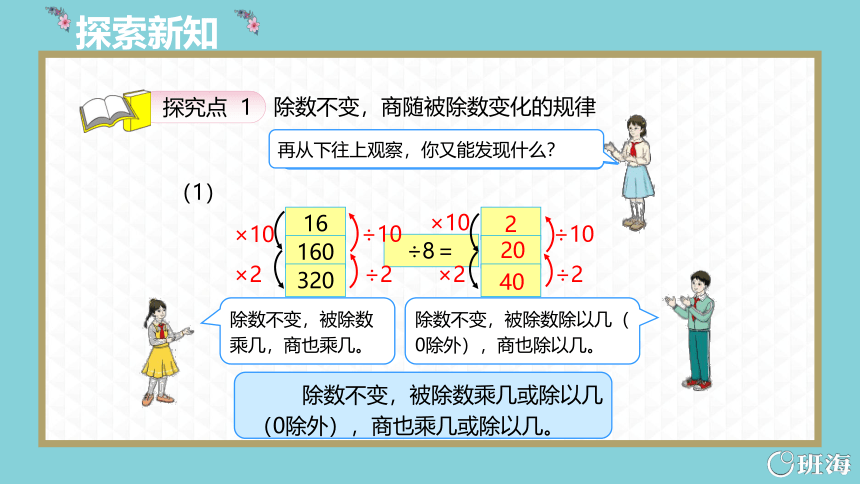
再从下往上观察,你又能发现什么?
(1)
16
160
320
÷8=
2
20
40
×10
×10
×2
×2
÷10
÷10
÷2
÷2
除数不变,被除数除以几(0除外),商也除以几。
除数不变,被除数
乘几,商也乘几。
探究点 1
除数不变,商随被除数变化的规律
除数不变,被除数乘几或除以几(0除外),商也乘几或除以几。
探索新知
方法归纳:
除数不变,商随被除数变化的规律:
除数不变,被除数乘(或除以)几(0除外),商也乘(或除以)几。
探索新知
被除数不变,除数除
以几,商就乘几。
请你把两个发现合并成一句话。
仔细观察第(2)组,你能发现什么?
再从下往上观察,你又能发现什么?
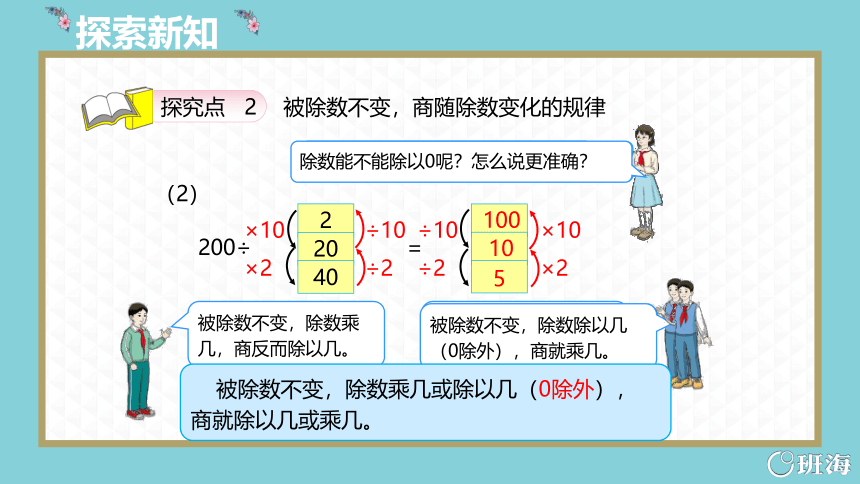
除数能不能除以0呢?怎么说更准确?
=
(2)
2
20
40
200÷
100
10
5
×10
×2
÷10
÷2
÷10
÷2
×10
×2
被除数不变,除数乘
几,商反而除以几。
被除数不变,除数除以几
(0除外),商就乘几。
被除数不变,除数乘几或除以几(0除外),
商就除以几或乘几。
探究点 2
被除数不变,商随除数变化的规律
探索新知
方法归纳:
被除数不变,商随除数变化的规律:
被除数不变,除数乘(或除以)几(0除外),商就除以(或乘)几。
探索新知
被除数和除数都乘或除以一个相同的数(0除外),商不变。
(3)计算并观察下面的题。
6
60
600
6000
÷
÷
÷
÷
3
30
300
3000
=
=
=
=
2
2
2
2
先从上往下观察,再从下
往上观察,你发现了什么?
探究点 3
商不变的规律
举例验证!
探索新知
商不变的规律:
被除数和除数同乘(或除以)相同的数(0除外),商不变。
归纳总结:
探索新知
除法计算很有趣,商的变化有规律;
变与不变要看准,被除数、除数是关键;
两者仅有一个变,商也同时跟着变;
同乘同除相同数,这时得商皆不变。
典题精讲
根据每组题中第1题的商,写出下面两题的商。
72÷9=
720÷90=
7200÷900=
36÷3=
360÷30=
3600÷300=
80÷4=
800÷40=
8000÷400=
8
8
8
12
12
12
20
20
20
易错提醒
判断。
(1)864÷24=(864+10)÷(24+10) ( )
(2)80÷16=(80×4)÷(16÷4) ( )
×
×
辨析:被除数和除数同时乘以或者同时除以不为0的数,商不变。
学以致用
03
小试牛刀
1. 12÷6=
120÷6=
1200÷6=
我的发现:除数不变,被除数( ),
商就( )。
2
20
200
乘(或除以)几(0除外)
乘(或除以)相同的数
小试牛刀
2.计算下面各题。
800÷2=
800÷20=
800÷200=
我的发现:被除数不变,除数( ),
商就( )。
除以(或乘)相同的数
乘(或除以)几(0除外)
4
40
400
小试牛刀
3. 45÷9=
450÷90=
4500÷900=
我的发现:被除数和除数( ),
商( )。
同时乘(或除以)相同的数(0除外)
不变
5
5
5
小试牛刀
4.根据210÷15=14直接写出下面各题的商。
210÷3= 210÷5= 210÷30=
630÷15= 420÷15= 840÷15=
420÷30= 630÷45= 840÷60=
14
56
28
42
7
42
70
14
14
课堂小结
04
归纳总结:
商的变化规律:
规律一:除数不变,被除数乘几或除以几(0除外),商也乘几或除以几。
规律二:被除数不变,除数乘几或除以几(0除外),商就除以几或乘几。
规律三:被除数和除数都乘或除以一个相同的数(0除外),商不变。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(↓↓观看介绍视频↓↓)
商的变化规律
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
课前导入
学以致用
新课精讲
课堂小结
01
02
03
04
目 录
课前导入
01
情景导入
花果山风景秀丽,气候宜人,那里住着一群猴子。有一天,猴王让一只小猴分桃子。猴王说:“给你4个桃子,平均分给2只猴吧。”小猴听了,连连摇头说:“太少了,太少了。”猴王又说:“好吧,给你40个桃子,平均分给20只猴,怎么样?”小猴得寸进尺,挠挠头皮,试探地说:“大王,再多给点行不行啊?”猴王一拍桌子,显示出慷慨大度的样子说:“那好吧,给你400个桃子,平均分给200只小猴,你总该满意了吧?” 小猴子连忙说:“好了、好了”!猴王听了哈哈大笑。
猴王分桃的故事
你知道猴王为什么笑吗?
新课精讲
02
探索新知
你能把两个发现合并成一句话吗?
先观察第(1)组,你能发现什么?
再从下往上观察,你又能发现什么?
(1)
16
160
320
÷8=
2
20
40
×10
×10
×2
×2
÷10
÷10
÷2
÷2
除数不变,被除数除以几(0除外),商也除以几。
除数不变,被除数
乘几,商也乘几。
探究点 1
除数不变,商随被除数变化的规律
除数不变,被除数乘几或除以几(0除外),商也乘几或除以几。
探索新知
方法归纳:
除数不变,商随被除数变化的规律:
除数不变,被除数乘(或除以)几(0除外),商也乘(或除以)几。
探索新知
被除数不变,除数除
以几,商就乘几。
请你把两个发现合并成一句话。
仔细观察第(2)组,你能发现什么?
再从下往上观察,你又能发现什么?
除数能不能除以0呢?怎么说更准确?
=
(2)
2
20
40
200÷
100
10
5
×10
×2
÷10
÷2
÷10
÷2
×10
×2
被除数不变,除数乘
几,商反而除以几。
被除数不变,除数除以几
(0除外),商就乘几。
被除数不变,除数乘几或除以几(0除外),
商就除以几或乘几。
探究点 2
被除数不变,商随除数变化的规律
探索新知
方法归纳:
被除数不变,商随除数变化的规律:
被除数不变,除数乘(或除以)几(0除外),商就除以(或乘)几。
探索新知
被除数和除数都乘或除以一个相同的数(0除外),商不变。
(3)计算并观察下面的题。
6
60
600
6000
÷
÷
÷
÷
3
30
300
3000
=
=
=
=
2
2
2
2
先从上往下观察,再从下
往上观察,你发现了什么?
探究点 3
商不变的规律
举例验证!
探索新知
商不变的规律:
被除数和除数同乘(或除以)相同的数(0除外),商不变。
归纳总结:
探索新知
除法计算很有趣,商的变化有规律;
变与不变要看准,被除数、除数是关键;
两者仅有一个变,商也同时跟着变;
同乘同除相同数,这时得商皆不变。
典题精讲
根据每组题中第1题的商,写出下面两题的商。
72÷9=
720÷90=
7200÷900=
36÷3=
360÷30=
3600÷300=
80÷4=
800÷40=
8000÷400=
8
8
8
12
12
12
20
20
20
易错提醒
判断。
(1)864÷24=(864+10)÷(24+10) ( )
(2)80÷16=(80×4)÷(16÷4) ( )
×
×
辨析:被除数和除数同时乘以或者同时除以不为0的数,商不变。
学以致用
03
小试牛刀
1. 12÷6=
120÷6=
1200÷6=
我的发现:除数不变,被除数( ),
商就( )。
2
20
200
乘(或除以)几(0除外)
乘(或除以)相同的数
小试牛刀
2.计算下面各题。
800÷2=
800÷20=
800÷200=
我的发现:被除数不变,除数( ),
商就( )。
除以(或乘)相同的数
乘(或除以)几(0除外)
4
40
400
小试牛刀
3. 45÷9=
450÷90=
4500÷900=
我的发现:被除数和除数( ),
商( )。
同时乘(或除以)相同的数(0除外)
不变
5
5
5
小试牛刀
4.根据210÷15=14直接写出下面各题的商。
210÷3= 210÷5= 210÷30=
630÷15= 420÷15= 840÷15=
420÷30= 630÷45= 840÷60=
14
56
28
42
7
42
70
14
14
课堂小结
04
归纳总结:
商的变化规律:
规律一:除数不变,被除数乘几或除以几(0除外),商也乘几或除以几。
规律二:被除数不变,除数乘几或除以几(0除外),商就除以几或乘几。
规律三:被除数和除数都乘或除以一个相同的数(0除外),商不变。
同学们,下节课见!
一键发布配套作业 & AI智能精细批改
(↓↓观看介绍视频↓↓)
