人教版(新)八上-13.4 课题学习 最短路径问题【优质课件】
文档属性
| 名称 | 人教版(新)八上-13.4 课题学习 最短路径问题【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览




文档简介
(共20张PPT)
13.4 课题学习 最短路径问题
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
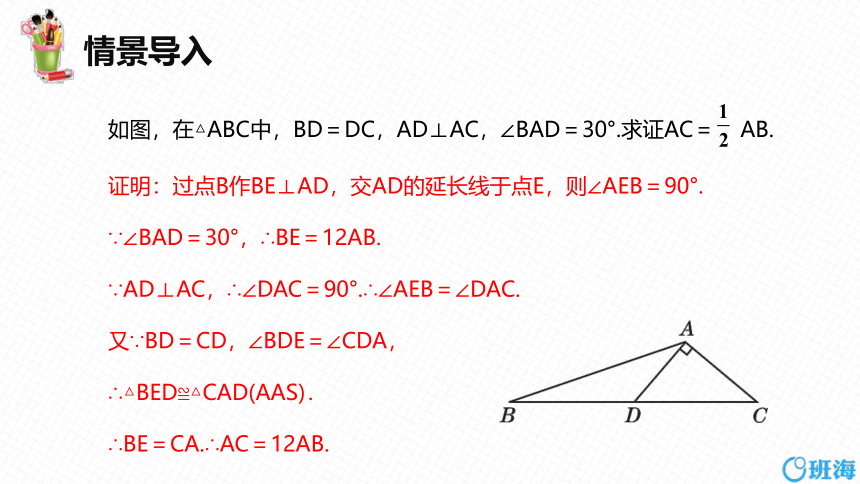
情景导入
如图,在△ABC中,BD=DC,AD⊥AC,∠BAD=30°.求证AC= AB.
证明:过点B作BE⊥AD,交AD的延长线于点E,则∠AEB=90°.
∵∠BAD=30°,∴BE=12AB.
∵AD⊥AC,∴∠DAC=90°.∴∠AEB=∠DAC.
又∵BD=CD,∠BDE=∠CDA,
∴△BED≌△CAD(AAS).
∴BE=CA.∴AC=12AB.
新课精讲
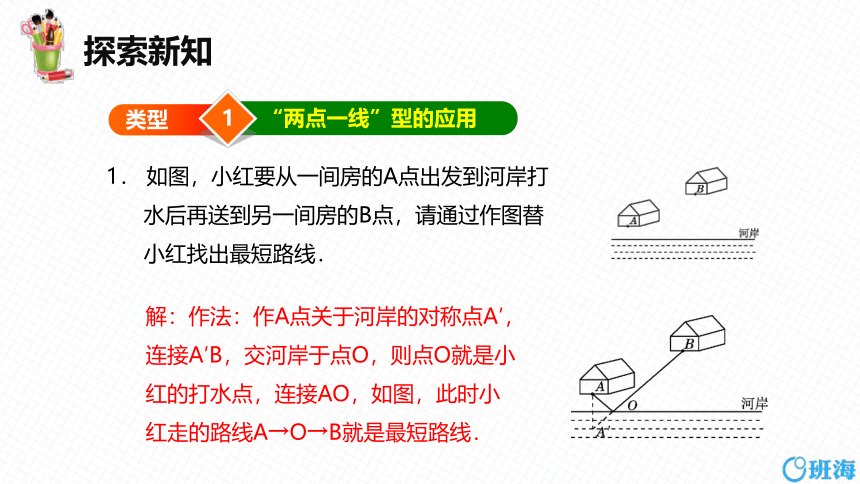
探索新知
1. 如图,小红要从一间房的A点出发到河岸打水后再送到另一间房的B点,请通过作图替小红找出最短路线.
1
类型
“两点一线”型的应用
解:作法:作A点关于河岸的对称点A′,连接A′B,交河岸于点O,则点O就是小红的打水点,连接AO,如图,此时小红走的路线A→O→B就是最短路线.
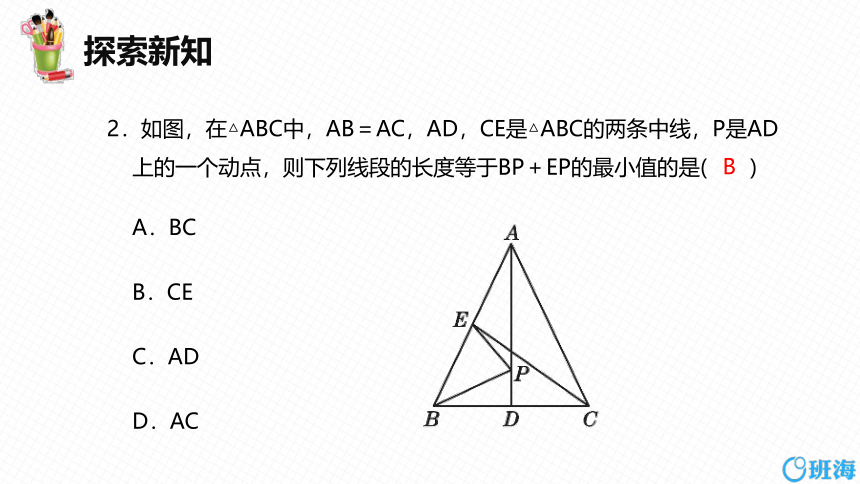
探索新知
2.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD
上的一个动点,则下列线段的长度等于BP+EP的最小值的是( )
A.BC
B.CE
C.AD
D.AC
B
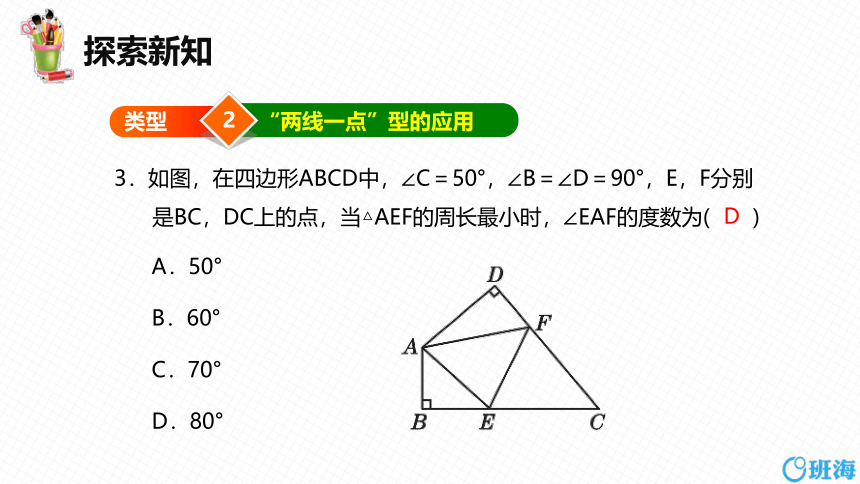
探索新知
3.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.50°
B.60°
C.70°
D.80°
D
2
类型
“两线一点”型的应用
探索新知
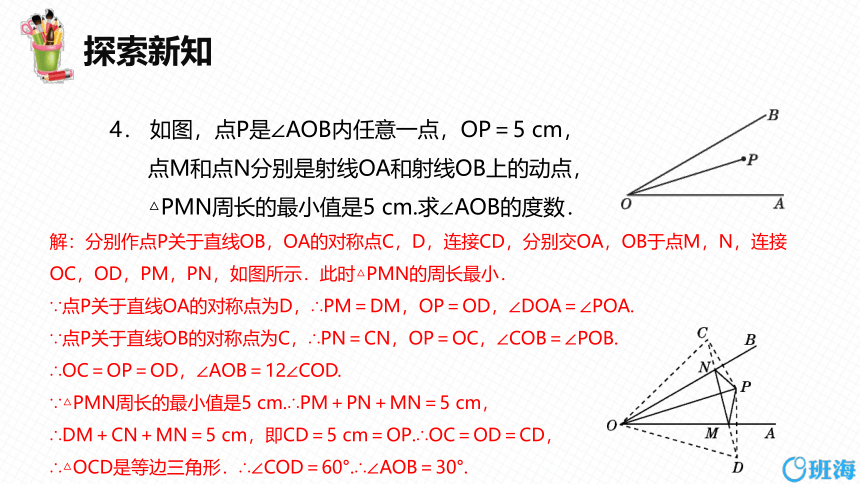
4. 如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5 cm.求∠AOB的度数.
解:分别作点P关于直线OB,OA的对称点C,D,连接CD,分别交OA,OB于点M,N,连接OC,OD,PM,PN,如图所示.此时△PMN的周长最小.
∵点P关于直线OA的对称点为D,∴PM=DM,OP=OD,∠DOA=∠POA.
∵点P关于直线OB的对称点为C,∴PN=CN,OP=OC,∠COB=∠POB.
∴OC=OP=OD,∠AOB=12∠COD.
∵△PMN周长的最小值是5 cm.∴PM+PN+MN=5 cm,
∴DM+CN+MN=5 cm,即CD=5 cm=OP.∴OC=OD=CD,
∴△OCD是等边三角形.∴∠COD=60°.∴∠AOB=30°.
探索新知
5.茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上.请你帮助他设计一条行走路线,使其所走的总路程最短.
3
类型
“两点两线”型的应用
(2)连接C1D1,分别交OA,OB于点P,Q,连接CP,DQ,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.
解:如图所示.
作法:(1)作C点关于OA的对称点C1,D点关于OB的对称点D1;
探索新知
6.如图,荆州护城河在CC′处直角转弯,河宽均为5 m,A,B到外河岸的距离都为5 m,从A处到达B处,需经两座桥:DD′,EE′(桥宽不计).设护城河及两座桥都是东西、南北方向的,如何架桥可使路程最短?
解:如图所示.分别由A,B向外河岸作垂线,垂足分别为F,G.连接GF,与内河岸相交于点E′,D′.
分别由E′,D′向外河岸引垂线段E′E,D′D,连接AD,BE,则DD′,EE′即为桥.沿A→D→D′→E′→E→B的路线行走路程最短.
探索新知
7.如图,村庄A,B位于一条小河的两侧,若河岸a,b彼此平行,现在要建一座与河岸垂直的桥CD.问桥址应如何选择,才能使A村到B村的路程最短?
解:(1)过点A作AP⊥a,并在AP上向下截取AA′,使AA′=河的宽度;
(2)连接A′B交b于点D;
(3)过点D作DC∥AA′交a于点C.
则CD即为桥的位置.图略.
学以致用
小试牛刀
1.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,
不是轴对称图形的是( )
D
2.观察图①~④中的左右两个图形,它们是否成轴对称?如果是,请
画出其对称轴.
解:题图①②③中的左右两个图形成轴对称,题图④中的左右两个图形不成轴对称(画对称轴略).
小试牛刀
3.如图,将长方形纸片ABCD沿AE向上折叠,使点B落
在DC边上的点F处.若△AFD的周长为24 cm,△ECF
的周长为8 cm,求长方形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
∴AB=AF,BE=FE. ∵△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
∴长方形纸片ABCD的周长为:
AD+DC+BC+AB=AD+DF+FC+CE+BE+AB
=(AD+DF+AF)+(FC+CE+FE)=24+8=32(cm).
小试牛刀
4.在△ABC中,AB=AC,D为直线BC上一点,E为直
线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=________,β=________;
②求α,β之间的关系式.
20°
10°
设∠ABC=x,∠ADE=y,
则∠ACB=x,∠AED=y. 在△DEC中,y=β+x;
在△ABD中,α+x=y+β,∴α=2β.
小试牛刀
(2)是否存在不同于以上②中的α,β之间的关系式?若
存在,求出这个关系式(求出一个即可);若不存在,
请说明理由.
存在.如图:
当点E在CA的延长线上,点D在线段BC上时,
设∠ABC=x,∠ADE=y,
则∠ACB=x,∠AED=y.
在△ABD中,x+α=β-y;
在△DEC中,x+y+β=180°,
小试牛刀
5.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证△ABE≌△DCE;
证明:∵四边形ABCD是正方形,∴AB=BC=CD,
∠ABC=∠DCB=90°.
∵△EBC是等边三角形,∴EB=BC=EC,∠EBC=∠ECB=60°.
∴∠EBA=∠ECD=30°.
在△ABE和△DCE中,
∴△ABE≌△DCE(SAS).
小试牛刀
(2)求∠AED的度数.
解:由(1)知AB=BE,
∠ABE=30°,
∴∠BAE=∠BEA=75°.
同理,∠CDE=∠CED=75°.
∵△BEC是等边三角形,
∴∠BEC=60°. ∴∠AED=360°-75°-75°-60°=150°.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
13.4 课题学习 最短路径问题
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课前导入
情景导入
如图,在△ABC中,BD=DC,AD⊥AC,∠BAD=30°.求证AC= AB.
证明:过点B作BE⊥AD,交AD的延长线于点E,则∠AEB=90°.
∵∠BAD=30°,∴BE=12AB.
∵AD⊥AC,∴∠DAC=90°.∴∠AEB=∠DAC.
又∵BD=CD,∠BDE=∠CDA,
∴△BED≌△CAD(AAS).
∴BE=CA.∴AC=12AB.
新课精讲
探索新知
1. 如图,小红要从一间房的A点出发到河岸打水后再送到另一间房的B点,请通过作图替小红找出最短路线.
1
类型
“两点一线”型的应用
解:作法:作A点关于河岸的对称点A′,连接A′B,交河岸于点O,则点O就是小红的打水点,连接AO,如图,此时小红走的路线A→O→B就是最短路线.
探索新知
2.如图,在△ABC中,AB=AC,AD,CE是△ABC的两条中线,P是AD
上的一个动点,则下列线段的长度等于BP+EP的最小值的是( )
A.BC
B.CE
C.AD
D.AC
B
探索新知
3.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.50°
B.60°
C.70°
D.80°
D
2
类型
“两线一点”型的应用
探索新知
4. 如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5 cm.求∠AOB的度数.
解:分别作点P关于直线OB,OA的对称点C,D,连接CD,分别交OA,OB于点M,N,连接OC,OD,PM,PN,如图所示.此时△PMN的周长最小.
∵点P关于直线OA的对称点为D,∴PM=DM,OP=OD,∠DOA=∠POA.
∵点P关于直线OB的对称点为C,∴PN=CN,OP=OC,∠COB=∠POB.
∴OC=OP=OD,∠AOB=12∠COD.
∵△PMN周长的最小值是5 cm.∴PM+PN+MN=5 cm,
∴DM+CN+MN=5 cm,即CD=5 cm=OP.∴OC=OD=CD,
∴△OCD是等边三角形.∴∠COD=60°.∴∠AOB=30°.
探索新知
5.茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上.请你帮助他设计一条行走路线,使其所走的总路程最短.
3
类型
“两点两线”型的应用
(2)连接C1D1,分别交OA,OB于点P,Q,连接CP,DQ,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.
解:如图所示.
作法:(1)作C点关于OA的对称点C1,D点关于OB的对称点D1;
探索新知
6.如图,荆州护城河在CC′处直角转弯,河宽均为5 m,A,B到外河岸的距离都为5 m,从A处到达B处,需经两座桥:DD′,EE′(桥宽不计).设护城河及两座桥都是东西、南北方向的,如何架桥可使路程最短?
解:如图所示.分别由A,B向外河岸作垂线,垂足分别为F,G.连接GF,与内河岸相交于点E′,D′.
分别由E′,D′向外河岸引垂线段E′E,D′D,连接AD,BE,则DD′,EE′即为桥.沿A→D→D′→E′→E→B的路线行走路程最短.
探索新知
7.如图,村庄A,B位于一条小河的两侧,若河岸a,b彼此平行,现在要建一座与河岸垂直的桥CD.问桥址应如何选择,才能使A村到B村的路程最短?
解:(1)过点A作AP⊥a,并在AP上向下截取AA′,使AA′=河的宽度;
(2)连接A′B交b于点D;
(3)过点D作DC∥AA′交a于点C.
则CD即为桥的位置.图略.
学以致用
小试牛刀
1.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,
不是轴对称图形的是( )
D
2.观察图①~④中的左右两个图形,它们是否成轴对称?如果是,请
画出其对称轴.
解:题图①②③中的左右两个图形成轴对称,题图④中的左右两个图形不成轴对称(画对称轴略).
小试牛刀
3.如图,将长方形纸片ABCD沿AE向上折叠,使点B落
在DC边上的点F处.若△AFD的周长为24 cm,△ECF
的周长为8 cm,求长方形纸片ABCD的周长.
解:由题意可知,△ABE和△AFE关于直线AE成轴对称,
∴AB=AF,BE=FE. ∵△AFD的周长为24 cm,△ECF的周长为8 cm,
即AD+DF+AF=24 cm,FC+CE+FE=8 cm,
∴长方形纸片ABCD的周长为:
AD+DC+BC+AB=AD+DF+FC+CE+BE+AB
=(AD+DF+AF)+(FC+CE+FE)=24+8=32(cm).
小试牛刀
4.在△ABC中,AB=AC,D为直线BC上一点,E为直
线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=________,β=________;
②求α,β之间的关系式.
20°
10°
设∠ABC=x,∠ADE=y,
则∠ACB=x,∠AED=y. 在△DEC中,y=β+x;
在△ABD中,α+x=y+β,∴α=2β.
小试牛刀
(2)是否存在不同于以上②中的α,β之间的关系式?若
存在,求出这个关系式(求出一个即可);若不存在,
请说明理由.
存在.如图:
当点E在CA的延长线上,点D在线段BC上时,
设∠ABC=x,∠ADE=y,
则∠ACB=x,∠AED=y.
在△ABD中,x+α=β-y;
在△DEC中,x+y+β=180°,
小试牛刀
5.如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证△ABE≌△DCE;
证明:∵四边形ABCD是正方形,∴AB=BC=CD,
∠ABC=∠DCB=90°.
∵△EBC是等边三角形,∴EB=BC=EC,∠EBC=∠ECB=60°.
∴∠EBA=∠ECD=30°.
在△ABE和△DCE中,
∴△ABE≌△DCE(SAS).
小试牛刀
(2)求∠AED的度数.
解:由(1)知AB=BE,
∠ABE=30°,
∴∠BAE=∠BEA=75°.
同理,∠CDE=∠CED=75°.
∵△BEC是等边三角形,
∴∠BEC=60°. ∴∠AED=360°-75°-75°-60°=150°.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
