人教版(新)八上-14.1.1 同底数幂的乘法【优质课件】
文档属性
| 名称 | 人教版(新)八上-14.1.1 同底数幂的乘法【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览










文档简介
(共31张PPT)
14.1.1
同底数幂的乘法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
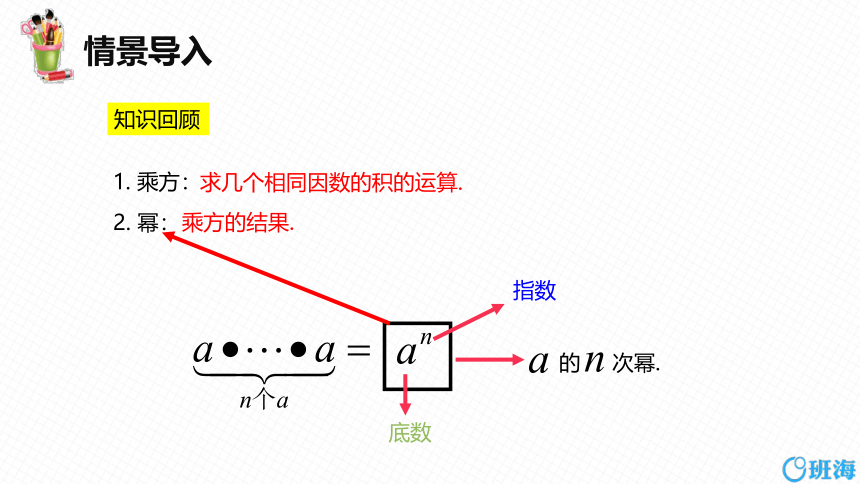
情景导入
底数
指数
的 次幂.
求几个相同因数的积的运算.
1. 乘方:
2. 幂:
乘方的结果.
知识回顾
新课精讲
探索新知
1
知识点
一种电子计算机每秒可进行1千万亿(1015) 次运算,它工作103 s可进行多少次 运算?
它工作103 s可进行运算的次数为1015 ×103. 怎样计算1015 ×103呢?
问 题(一)
同底数幂的乘法的法则
探索新知
根据乘方的意义可知
1015 ×103 =
=1018.
探索新知
问 题(二)
根据乘方的意义填空,观察计算结果,你能发现什么规律?
(1) 25 × 22 = 2( );
(2) a3 · a2=a ( ) ;
(3) 5m × 5n = 5 ( ).
5
7
m+n
探索新知
猜想: am · an=am+n (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
你们真棒,你的猜想是正确的!
·
探索新知
am · an =
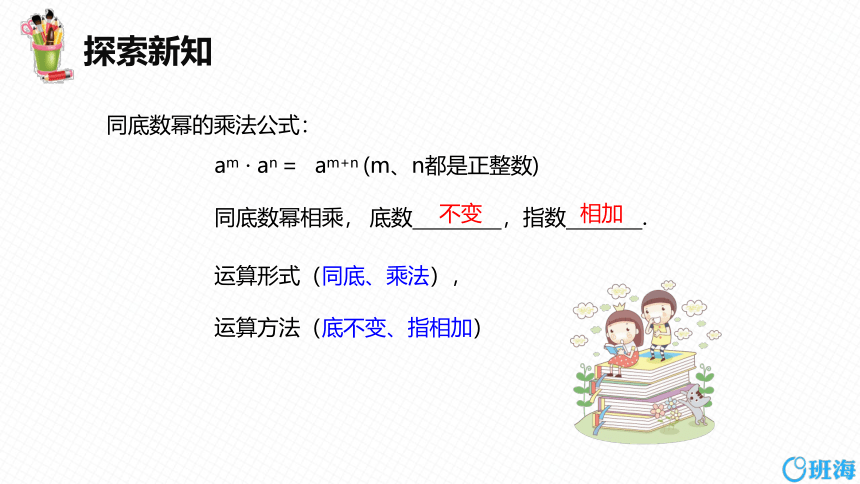
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法公式:
am+n (m、n都是正整数)
运算形式(同底、乘法),
运算方法(底不变、指相加)
探索新知
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
am·an·ap =
(m,n,p都是正整数)
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
am+n+p
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
am·an·ap
n个a
m个a
p个a
=am+n+p
或
探索新知
计算:
(1) x2 x5; (2) a a6;
(3) (- 2) ×(- 2)4 ×(- 2)3; (4) xm x3m+1.
例1
=x2+5
=x7
=a1+6
=a7
= (- 2)1+4+3
= (- 2)8=256
=xm+3m+1
=x4m+1.
探索新知
1.同底数幂相乘时,指数是相加的;
2.不能忽略指数为1的情况;
3.公式中的a可为一个数、单项式或多项式,如:
(x -y)m (x -y)n = (x -y) m+n .
总 结
典题精讲
1.计算x2 x3的结果为( )
A.2x2 B.x5
C.2x3 D.x6
2.计算(-y2) y3的结果是( )
A.y5 B.-y5
C.y6 D.-y6
B
B
典题精讲
3.下列各式能用同底数幂的乘法法则进行计算的是( )
A.(x+y)2 (x-y)3
B.(-x-y)(x+y) 2
C.(x+y) 2+(x+y) 3
D.-(x-y) 2 (-x-y) 3
B
典题精讲
4.计算:
(1)b5 b; (2)
(3)a2 a6 ; (4)y2n yn+1 .
解:
=b6
解:
=
解:
= a8
解:
= y3n+1
探索新知
2
知识点
同底数幂的乘法法则的应用
同底数幂的乘法法则既可以正用,也可以逆用. 当其逆用时am+n =am an 。
探索新知
已知am=9,an=81,求am+n的值.
例2
导引:
将同底数幂的乘法法则逆用,可求出值.
解:
am+n
=am an
=9×81
=729.
探索新知
当幂的指数是和的形式时,可逆向运用同底数幂的乘法法则,将其转化为同底数幂相乘的形式,然后把幂作为一个整体代入变形后的幂的运算式中求解.
总 结
典题精讲
1.a2 016可以写成( )
A.a2 010+a6 B. a2 010 a6
C.a2 010 a D.a2 008 a2 008
2.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科
学记数法表示该市2014年底机动车的数量是( )
A.2.3×105辆 B.3.2×105辆
C.2.3×106辆 D.3.2×106辆
B
C
典题精讲
3.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
已知am=2,an=3,求下列各式的值:
am +1;
an +2;
am +n+1.
3
5
6
2a
3a2
6a
学以致用
小试牛刀
1. 等于( ).
A. B.
C. D.
B
2. 等于( ).
A. B.
C. D.
C
小试牛刀
3.计算:(﹣t)6 t2=( )
A.t8 B.-t8
C.﹣t12 D. t12
A
4.
x6
x5
小试牛刀
5.计算.
小试牛刀
6.已知xa+b=6,xb=3,求xa 求xa的值.
解:根据同底数幂的乘法法则求解.
xa
=xa+b÷xb
=6÷3
=2.
小试牛刀
7.如果 ,且 ,求m,n的值.
解:利用同底数幂的乘法法则来解答
因为 ,又因为
再利用 和 ,求出m = 4,n = - 4
小试牛刀
8.已知4×2a×2a+1=29,且2a+b=8,求ab的值.
解:由题意得,2a+3=9,
解得:a=3,
则b=8﹣2a=8﹣6=2,
ab=9
课堂小结
课堂小结
同底数幂相乘,
底数不变, 指数相加
am · an = am+n (m、n正整数)
同底数幂的乘法
知识
方法
“特殊→一般→特殊”
例子 公式 应用
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.1.1
同底数幂的乘法
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
底数
指数
的 次幂.
求几个相同因数的积的运算.
1. 乘方:
2. 幂:
乘方的结果.
知识回顾
新课精讲
探索新知
1
知识点
一种电子计算机每秒可进行1千万亿(1015) 次运算,它工作103 s可进行多少次 运算?
它工作103 s可进行运算的次数为1015 ×103. 怎样计算1015 ×103呢?
问 题(一)
同底数幂的乘法的法则
探索新知
根据乘方的意义可知
1015 ×103 =
=1018.
探索新知
问 题(二)
根据乘方的意义填空,观察计算结果,你能发现什么规律?
(1) 25 × 22 = 2( );
(2) a3 · a2=a ( ) ;
(3) 5m × 5n = 5 ( ).
5
7
m+n
探索新知
猜想: am · an=am+n (当m、n都是正整数)
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
(aa…a)
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
你们真棒,你的猜想是正确的!
·
探索新知
am · an =
同底数幂相乘,
底数 ,指数 .
不变
相加
同底数幂的乘法公式:
am+n (m、n都是正整数)
运算形式(同底、乘法),
运算方法(底不变、指相加)
探索新知
当三个或三个以上同底数幂相乘时,是否也具有这一性质呢? 怎样用公式表示?
am·an·ap =
(m,n,p都是正整数)
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
am+n+p
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
am·an·ap
n个a
m个a
p个a
=am+n+p
或
探索新知
计算:
(1) x2 x5; (2) a a6;
(3) (- 2) ×(- 2)4 ×(- 2)3; (4) xm x3m+1.
例1
=x2+5
=x7
=a1+6
=a7
= (- 2)1+4+3
= (- 2)8=256
=xm+3m+1
=x4m+1.
探索新知
1.同底数幂相乘时,指数是相加的;
2.不能忽略指数为1的情况;
3.公式中的a可为一个数、单项式或多项式,如:
(x -y)m (x -y)n = (x -y) m+n .
总 结
典题精讲
1.计算x2 x3的结果为( )
A.2x2 B.x5
C.2x3 D.x6
2.计算(-y2) y3的结果是( )
A.y5 B.-y5
C.y6 D.-y6
B
B
典题精讲
3.下列各式能用同底数幂的乘法法则进行计算的是( )
A.(x+y)2 (x-y)3
B.(-x-y)(x+y) 2
C.(x+y) 2+(x+y) 3
D.-(x-y) 2 (-x-y) 3
B
典题精讲
4.计算:
(1)b5 b; (2)
(3)a2 a6 ; (4)y2n yn+1 .
解:
=b6
解:
=
解:
= a8
解:
= y3n+1
探索新知
2
知识点
同底数幂的乘法法则的应用
同底数幂的乘法法则既可以正用,也可以逆用. 当其逆用时am+n =am an 。
探索新知
已知am=9,an=81,求am+n的值.
例2
导引:
将同底数幂的乘法法则逆用,可求出值.
解:
am+n
=am an
=9×81
=729.
探索新知
当幂的指数是和的形式时,可逆向运用同底数幂的乘法法则,将其转化为同底数幂相乘的形式,然后把幂作为一个整体代入变形后的幂的运算式中求解.
总 结
典题精讲
1.a2 016可以写成( )
A.a2 010+a6 B. a2 010 a6
C.a2 010 a D.a2 008 a2 008
2.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科
学记数法表示该市2014年底机动车的数量是( )
A.2.3×105辆 B.3.2×105辆
C.2.3×106辆 D.3.2×106辆
B
C
典题精讲
3.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
已知am=2,an=3,求下列各式的值:
am +1;
an +2;
am +n+1.
3
5
6
2a
3a2
6a
学以致用
小试牛刀
1. 等于( ).
A. B.
C. D.
B
2. 等于( ).
A. B.
C. D.
C
小试牛刀
3.计算:(﹣t)6 t2=( )
A.t8 B.-t8
C.﹣t12 D. t12
A
4.
x6
x5
小试牛刀
5.计算.
小试牛刀
6.已知xa+b=6,xb=3,求xa 求xa的值.
解:根据同底数幂的乘法法则求解.
xa
=xa+b÷xb
=6÷3
=2.
小试牛刀
7.如果 ,且 ,求m,n的值.
解:利用同底数幂的乘法法则来解答
因为 ,又因为
再利用 和 ,求出m = 4,n = - 4
小试牛刀
8.已知4×2a×2a+1=29,且2a+b=8,求ab的值.
解:由题意得,2a+3=9,
解得:a=3,
则b=8﹣2a=8﹣6=2,
ab=9
课堂小结
课堂小结
同底数幂相乘,
底数不变, 指数相加
am · an = am+n (m、n正整数)
同底数幂的乘法
知识
方法
“特殊→一般→特殊”
例子 公式 应用
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
