人教版(新)八上-14.1.3 积的乘方【优质课件】
文档属性
| 名称 | 人教版(新)八上-14.1.3 积的乘方【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:51:21 | ||
图片预览











文档简介
(共31张PPT)
14.1.3 积的乘方
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.计算:
10×102× 103 =______ ,(x5 )2=_________.
x10
106
2.am·an= ( m,n都是正整数).
am+n
3.(am)n= (m,n都是正整数).
amn
同底数幂相乘,底数不变,指数相加.
法则
新课精讲
探索新知
1
知识点
积的乘方法则
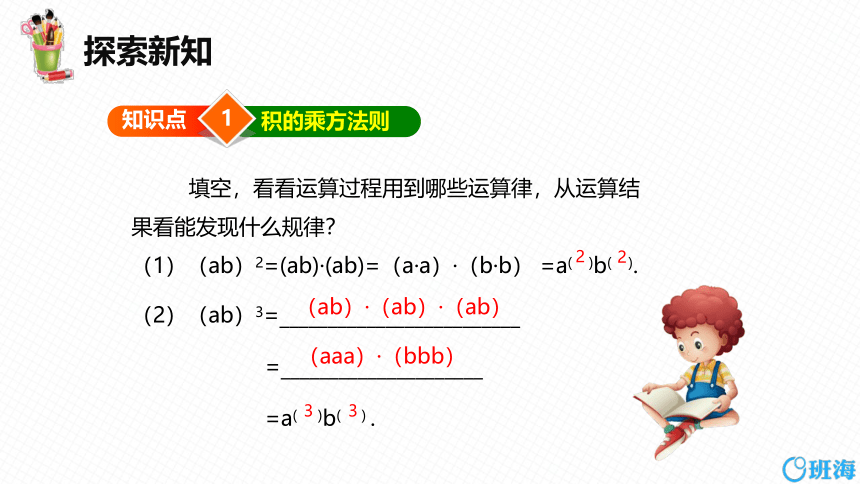
填空,看看运算过程用到哪些运算律,从运算结
果看能发现什么规律?
(1)(ab)2=(ab)·(ab)=(a·a)·(b·b) =a( )b( ).
(2)(ab)3=_________________________
=_____________________
=a( )b( ) .
2
2
(ab)·(ab)·(ab)
(aaa)·(bbb)
3
3
探索新知
n个a
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
= (a·a· ··· ·a) · (b·b· ··· ·b)
n个b
=anbn
思考:积的乘方(ab)n =
即:(ab)n=anbn (n为正整数)
探索新知
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
积的乘方法则
推广:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
探索新知
计算:
(2a)3; (2) (- 5b)3;
(3) (xy2)2; (4) (- 2x3)4.
例1
解: = 23 a3=8a3
解: = (- 5) 3 b 3 = - 125 b 3
解: =x2 (y2)2 =x2 y4
解: = (- 2)4 (x3)4 =16 x12
探索新知
运用积的乘方时,每个因式都要乘方,不能漏掉任何一个因式;系数应连同它的符号一起乘方,系数是-1时不可忽略.
总 结
典题精讲
1.下面的计算对不对?如果不对,应当怎样改正?
(1) (ab2)3=ab6; (2) (- 2a) 2 = - 4a2.
2.计算(-xy3) 2的结果是( )
A.x 2 y6 B.-x 2 y6
C.x 2 y9 D.-x 2 y9
不对,应该为 a3b6 ;
解:
A
不对,应该为4a 2 .
典题精讲
3.下列计算:
①(ab)2=ab2; ②(4ab)3=12a3b3;
③(-2x3)4=-16x12; ④ ,
其中正确的有( )
A.0个 B.1个
C.2个 D.3个
B
典题精讲
4.计算:
(1)(ab)4; (2)
(3)(- 3 × 102)3; (3) (2ab2)3.
解: =a4b4
解: =- x3y3;
解=-27×106或-2.7×107
解:=8a3b6
探索新知
2
知识点
积的乘方法则的应用
积的乘方法则既可以正用,也可以逆用.当其逆用时,即an bn =(a b)n (n为正整数) .
探索新知
用简便方法计算:
(1) (2)0.125 2015×(-8 2016).
例2
导引:
本例如果按照常规方法进行运算,(1)题比较麻烦,(2)题无法算出结果,因此需采用非常规方法进行计算.(1)观察该式的特点可知,需利用乘法的交换律和结合律,并逆用积的乘方法则计算;(2)82016=8 2015×8,故该式应逆用同底数幂的乘法和积的乘方法则计算.
探索新知
解:(1)
(2)0.1252015×(-8 2016) =-0.1252015×8 2016
=-0.125 2015×82015×8 =-(0.125×8)2015×8
=-12015×8=-8.
探索新知
底数互为倒数的两个幂相乘时,先通过逆用同底数幂的乘法法则化为幂指数相同的幂,然后逆用积的乘方法则计算,从而大大简化运算.
总 结
典题精讲
1.若(-2a1+xb2)3=-8a9b6,则x的值是( )
A.0 B.1 C.2 D.3
2.式子 的结果是( )
A. B.-2 C.2 D.
C
C
4.若n为正整数,且x2n=3,则(3x3n)2的值为________.
3.如果5n=a,4n=b,那么20n=________.
ab
243
探索新知
3
知识点
幂的混合运算
计算:(1)(xy2)3;
(2)(anb3n)2+(a2b6)n;
(3)[(a2) 3+(2a3) 2] 2.
例3
导引:
利用相关的幂的运算法则按先算乘方,再算乘除,最后算加减,有括号的先算括号里面的顺序进行计算;有同类项的要合并同类项,使结果最简.
探索新知
解:
(1)原式=x3y6;
(2)原式=a2nb6n+a2nb6n
=2a2nb6n;
(3)原式=(a6+4a6)2
=(5a6)2=25a12.
探索新知
幂的混合运算顺序与实数的混合运算顺序相同.
总 结
典题精讲
1.计算(-2a)2-3a2的结果是( )
A.-a2 B.a2
C.-5a2 D.5a2
2.计算(-4×103)2×(-2×103) 3的结果为( )
A.1.28×1017 B.-1.28×1017
C.4.8×1016 D.-2.4×1016
B
B
学以致用
小试牛刀
1.
已知am=2,bm=5,则(a2b)m=_________.
20
2.
计算p · p _______; =_______; ________.
p5
3.
计算(2a) =______; (a b) =_______;
(2x y) =_______.
8a3
a6b3
4x6y2
小试牛刀
4.
计算(xy ) 的结果是( )
xy6 B.x2y3
C.x2y6 D.x2y5
C
5.
计算 (-2a ) 的结果是( )
A.2a4 B.-2a4
C.4a4 D.-4a4
C
小试牛刀
6.
计算(﹣2a b ) ( )
﹣6a6b5 B.﹣8a6b6
C.﹣8a9b6 D.﹣6a9b6
C
7.
下列运算正确的是( )
A. B.
C. D.
C
小试牛刀
8.
计算.
(1)﹣t3×(﹣t)4×(﹣t)5
(2)(3a3)3+a3×a6﹣3a9
(3)
解:=t3+4+5=t12
解:=27a9+a9﹣3a9=25a9
解:
小试牛刀
9.
先化简,再求值: a3 (﹣b3)2 +( a b2)3 ,其中a= ,b=-4.
解:
a3 (﹣b3)2 +( a b2)3= a3b6 - a3 b6=
把a= ,b=-4带入得,
原式=
课堂小结
课堂小结
1.幂的运算的三个性质:
am·an=am+n (am)n=amn (ab)n=anbn ( m、n都为正整数)
2. 运用积的乘方法则时要注意什么?
每个因式都要“乘方”,还有符号问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.1.3 积的乘方
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.计算:
10×102× 103 =______ ,(x5 )2=_________.
x10
106
2.am·an= ( m,n都是正整数).
am+n
3.(am)n= (m,n都是正整数).
amn
同底数幂相乘,底数不变,指数相加.
法则
新课精讲
探索新知
1
知识点
积的乘方法则
填空,看看运算过程用到哪些运算律,从运算结
果看能发现什么规律?
(1)(ab)2=(ab)·(ab)=(a·a)·(b·b) =a( )b( ).
(2)(ab)3=_________________________
=_____________________
=a( )b( ) .
2
2
(ab)·(ab)·(ab)
(aaa)·(bbb)
3
3
探索新知
n个a
(ab) n= (ab)· (ab)· ··· ·(ab)
n个ab
= (a·a· ··· ·a) · (b·b· ··· ·b)
n个b
=anbn
思考:积的乘方(ab)n =
即:(ab)n=anbn (n为正整数)
探索新知
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
(ab)n = anbn (n为正整数)
积的乘方法则
推广:三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
探索新知
计算:
(2a)3; (2) (- 5b)3;
(3) (xy2)2; (4) (- 2x3)4.
例1
解: = 23 a3=8a3
解: = (- 5) 3 b 3 = - 125 b 3
解: =x2 (y2)2 =x2 y4
解: = (- 2)4 (x3)4 =16 x12
探索新知
运用积的乘方时,每个因式都要乘方,不能漏掉任何一个因式;系数应连同它的符号一起乘方,系数是-1时不可忽略.
总 结
典题精讲
1.下面的计算对不对?如果不对,应当怎样改正?
(1) (ab2)3=ab6; (2) (- 2a) 2 = - 4a2.
2.计算(-xy3) 2的结果是( )
A.x 2 y6 B.-x 2 y6
C.x 2 y9 D.-x 2 y9
不对,应该为 a3b6 ;
解:
A
不对,应该为4a 2 .
典题精讲
3.下列计算:
①(ab)2=ab2; ②(4ab)3=12a3b3;
③(-2x3)4=-16x12; ④ ,
其中正确的有( )
A.0个 B.1个
C.2个 D.3个
B
典题精讲
4.计算:
(1)(ab)4; (2)
(3)(- 3 × 102)3; (3) (2ab2)3.
解: =a4b4
解: =- x3y3;
解=-27×106或-2.7×107
解:=8a3b6
探索新知
2
知识点
积的乘方法则的应用
积的乘方法则既可以正用,也可以逆用.当其逆用时,即an bn =(a b)n (n为正整数) .
探索新知
用简便方法计算:
(1) (2)0.125 2015×(-8 2016).
例2
导引:
本例如果按照常规方法进行运算,(1)题比较麻烦,(2)题无法算出结果,因此需采用非常规方法进行计算.(1)观察该式的特点可知,需利用乘法的交换律和结合律,并逆用积的乘方法则计算;(2)82016=8 2015×8,故该式应逆用同底数幂的乘法和积的乘方法则计算.
探索新知
解:(1)
(2)0.1252015×(-8 2016) =-0.1252015×8 2016
=-0.125 2015×82015×8 =-(0.125×8)2015×8
=-12015×8=-8.
探索新知
底数互为倒数的两个幂相乘时,先通过逆用同底数幂的乘法法则化为幂指数相同的幂,然后逆用积的乘方法则计算,从而大大简化运算.
总 结
典题精讲
1.若(-2a1+xb2)3=-8a9b6,则x的值是( )
A.0 B.1 C.2 D.3
2.式子 的结果是( )
A. B.-2 C.2 D.
C
C
4.若n为正整数,且x2n=3,则(3x3n)2的值为________.
3.如果5n=a,4n=b,那么20n=________.
ab
243
探索新知
3
知识点
幂的混合运算
计算:(1)(xy2)3;
(2)(anb3n)2+(a2b6)n;
(3)[(a2) 3+(2a3) 2] 2.
例3
导引:
利用相关的幂的运算法则按先算乘方,再算乘除,最后算加减,有括号的先算括号里面的顺序进行计算;有同类项的要合并同类项,使结果最简.
探索新知
解:
(1)原式=x3y6;
(2)原式=a2nb6n+a2nb6n
=2a2nb6n;
(3)原式=(a6+4a6)2
=(5a6)2=25a12.
探索新知
幂的混合运算顺序与实数的混合运算顺序相同.
总 结
典题精讲
1.计算(-2a)2-3a2的结果是( )
A.-a2 B.a2
C.-5a2 D.5a2
2.计算(-4×103)2×(-2×103) 3的结果为( )
A.1.28×1017 B.-1.28×1017
C.4.8×1016 D.-2.4×1016
B
B
学以致用
小试牛刀
1.
已知am=2,bm=5,则(a2b)m=_________.
20
2.
计算p · p _______; =_______; ________.
p5
3.
计算(2a) =______; (a b) =_______;
(2x y) =_______.
8a3
a6b3
4x6y2
小试牛刀
4.
计算(xy ) 的结果是( )
xy6 B.x2y3
C.x2y6 D.x2y5
C
5.
计算 (-2a ) 的结果是( )
A.2a4 B.-2a4
C.4a4 D.-4a4
C
小试牛刀
6.
计算(﹣2a b ) ( )
﹣6a6b5 B.﹣8a6b6
C.﹣8a9b6 D.﹣6a9b6
C
7.
下列运算正确的是( )
A. B.
C. D.
C
小试牛刀
8.
计算.
(1)﹣t3×(﹣t)4×(﹣t)5
(2)(3a3)3+a3×a6﹣3a9
(3)
解:=t3+4+5=t12
解:=27a9+a9﹣3a9=25a9
解:
小试牛刀
9.
先化简,再求值: a3 (﹣b3)2 +( a b2)3 ,其中a= ,b=-4.
解:
a3 (﹣b3)2 +( a b2)3= a3b6 - a3 b6=
把a= ,b=-4带入得,
原式=
课堂小结
课堂小结
1.幂的运算的三个性质:
am·an=am+n (am)n=amn (ab)n=anbn ( m、n都为正整数)
2. 运用积的乘方法则时要注意什么?
每个因式都要“乘方”,还有符号问题.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
