人教版(新)八上-14.2.2 完全平方公式 第二课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-14.2.2 完全平方公式 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:52:06 | ||
图片预览











文档简介
(共30张PPT)
14.2.2 完全平方公式
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
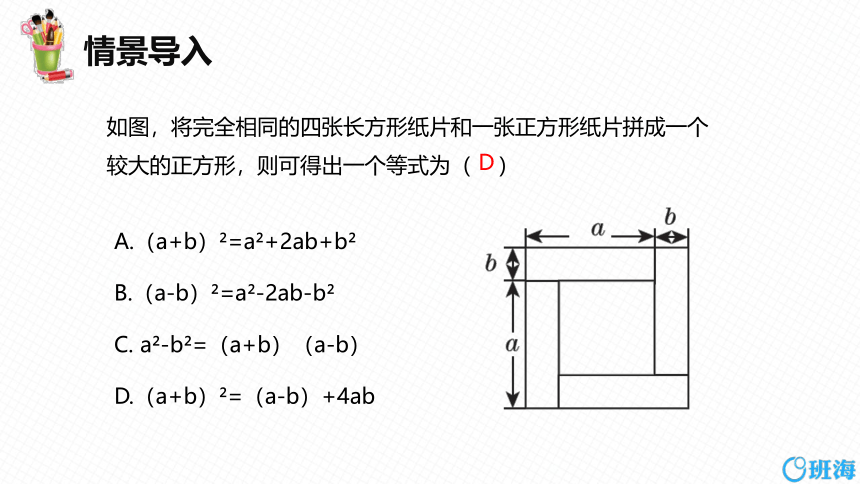
情景导入
如图,将完全相同的四张长方形纸片和一张正方形纸片拼成一个较大的正方形,则可得出一个等式为( )
D
A.(a+b) =a +2ab+b
B.(a-b) =a -2ab-b
C. a -b =(a+b)(a-b)
D.(a+b) =(a-b)+4ab
新课精讲
探索新知
1
知识点
添括号法则
运用乘法公式计算,有时要在式子中添括号.在第二章中,我们学过去括号法则,即
a+ ( b + c)=a + b + c;
a -(b +c)=a - b - c.
反过来,就得到添括号法则:
a + b + c = a+ ( b + c);
a - b - c = a -(b +c).
探索新知
也就是说,添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
归 纳
探索新知
例1
(1)下列各式中,成立的是( )
A.-x+y=-(x+y)
B.-3x+8=-3(x+8)
C.2-5x=-(5x-2)
D.-2-5x+y=-(2-5x+y)
C
因为-x+y=-(x-y),所以A选项错误;因为-3x+8=-(3x-8),所以B选项错误;因为2-5x=-(5x-2),所以C选项正确;因为-2-5x+y=-(2+5x-y),所以D选项错误.
导引:
探索新知
(2)下面添括号正确的是( )
A.2a-3b+c- =-(-2a+3b-c+ )
B.x2-2x-y+2x3=-(2x-y)-(-x2-2x3)
C.(a-b)(b-c)(c-a)=[-(a-b)][-(b-c)][-(c-a)]
D.(a-b-c)(a+b-c)=[a-(b-c)][a+(b-c)]
A
导引:
因为2a-3b+c- =-(-2a+3b-c+ ),所以A选项正确;因为x2-2x-y+2x3=-(2x+y)-(-x2-2x3),所以B选项错误;因为(a-b)(b-c)(c-a)=[-(-a+b)][-(-b+c)][-(-c+a)],所以C选项错误;因为(a-b-c)(a+b-c) =[a-(b+c)][a+(b-c)],所以D选项错误.
探索新知
(1)添括号只是一个变形,不改变式子的值.
(2)添括号是否正确,可利用去括号检验.
(3)添括号时,如果括号前面是负号,括到括号里的各项都改变符号,而不是只改变括号里的第一项的符号.
(4)根据题意需要适当地把某几项括到一起,不要随意地乱添加括号.
总 结
典题精讲
1.下列各式添括号正确的是( )
A.-x+y=-(y-x) B.x-y=-(x+y)
C.10-m=5(2-m) D.3-2a=-(2a-3)
D
2.下列添括号正确的是( )
A.a-b+c=a+(b+c) B.m+p-q=m-(p+q)
C.a-b-c+d=a-(b+c-d) D.x2-x+y=-(x2+x-y)
C
探索新知
例2
运用乘法公式计算:
(1)(x + 2y-3)(x - 2y + 3)
解: = [x + (2y-3)][x -(2y-3)]
= x2 - (2y - 3) 2
= x2 -(4y 2 - 12y + 9)
= x2 - 4y 2 + 12y - 9;
探索新知
解:= (a + b ) 2 + 2(a + b )c + c2
= a2 + 2a b + b 2 + 2ac + 2 b c + c2
= a2 + b 2 + c2 + 2a b + 2ac + 2 b c .
有些整式相乘需要先作适当变形,然后再用公式.
(2) (a + b + c)2.
探索新知
本题运用了整体思想求解.对于平方式中底数是三项的多项式,通过添括号将其中任意两项视为一个整体,就符合完全平方公式特点;对于两个乘积式中的三项或四项的多项式,可将符号相同的项及符号相反的项分别添括号视为一个整体,可化成平方差公式的形式,通过平方差公式展开再利用完全平方公式展开,最后合并可得结果.
总 结
典题精讲
1.下列添括号错误的是( )
A.a2-b2-b+a=a2-b2+(a-b)
B.(a+b+c)(a-b-c)=[a+(b+c)][a-(b+c)]
C.a-b+c-d=(a-d)+(c-b)
D.a-b=-(b+a)
D
典题精讲
2.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2
B.[x+(3y+1)]2
C.[x+(3y-1)] [x-(3y-1)]
D.[(x-3y)+1)] [(x-3y)-1)]
C
学以致用
小试牛刀
1.若(-2x2)(3x2-ax-6)-3x3+x2中不含x的三次项,则a=________.
2.计算:(1)(- ab3)2=________;
(2)4 2 016×(-0.25) 2 017=________;
(3)(π- ) 0=________.
-0.25
1
a2b6
小试牛刀
3.下列计算结果是x2-6x+5的是( )
A.(x-2)(x-3) B.(x-6)(x+1)
C.(x-1)(x-5) D.(x+6)(x-1)
C
4.下列运算正确的是( )
A.x6÷x2=x3 B.x0=1
C.(2x3)2=2x6 D.-2a2 a3=-2a5.
D
小试牛刀
5.下列计算正确的是( )
A.(-x-y)(x+y)=x2-y2
B.(x-y)2=x2-y2
C.(x+3y)(x-3y)=x2-3y2
D.(-x+y)2=x2-2xy+y2
D
小试牛刀
6.计算:
(1)2 0172-2 016×2 018;
原式=2 0172-(2 017-1)×(2 017+1)
=2 0172-(2 0172-12)
=2 0172-2 0172+1
=1.
解:
小试牛刀
(2)
原式=
解:
小试牛刀
(3)1002-992+982-972+…+42-32+22-12.
原式=(1002-992)+(982-972) +…+(22-12)
=(100+99)×(100-99)+(98+97) ×(98-97)+…+(2+1)×(2-1)
=100+99+98+97+…+2+1
=
=5 050.
解:
小试牛刀
7.对任意正整数n,整式(3n+1)(3n-1)- (3-n)(3+n)是不是10的倍
数?为什么?
对任意正整数n,整式(3n+1) (3n-1)-(3-n)
(3+n)是10的倍数,理由如下:(3n+1) (3n-1)
-(3-n)(3+n)=(3n)2-1-(32-n2)=9n2-1-
9+n2=10n2-10=10(n2-1).
∵对任意正整数n,10(n2-1)是10的倍数,
∴(3n+1) (3n-1)-(3-n) (3+n)是10的倍数.
解:
小试牛刀
8.先化简,再求值:2(2x-1)(2x+1)-5x(-x+3y)+4x(-4x- y),
其中x=-1,y=2.
解:
原式=2(4x2-1)+5x2-15xy-16x2-10xy
=8x2-2+5x2-15xy-16x2-10xy
=-3x2-25xy-2.
当x=-1,y=2时,
原式=-3×(-1)2-25×(-1)×2-2=45.
小试牛刀
王老师在一次团体操队列队形设计中,先让全体队员排成一方阵(行与列的人数一样多的队形,且总人数不少于25人),人数正好够用,然后再进行各种队形变化,其中一个队形需分为5人一组,手执彩带变换图形,在讨论分组方案时,有人说现在的队员人数按5人一组分将多出3人,你说这可能吗?
9.
小试牛刀
总人数可能为(5n)2人,(5n+1)2人,(5n+2)2人,(5n+3)2人,(5n+4)2人.(n为正整数) (5n)2=5n 5n;
(5n+1)2=25n2+10n+1=5(5n2+2n)+1;
(5n+2)2=25n2+20n+4=5(5n2+4n)+4;
(5n+3)2=25n2+30n+9=5(5n2+6n+1)+4;
(5n+4)2=25n2+40n+16=5(5n2+8n+3)+1.
由此可见,无论哪一种情况总人数按每组5人分,要么不多出人数,要么多出的人数只可能是1人或4人,不可能是3人.
解:
课堂小结
课堂小结
在乘法公式中添括号的“两种技巧”:
(1)当两个三项式相乘,且它们只含相同项和相反项时,常常需通过添括号把相同项、相反项分别结合,一个化为“和”的形式,一个化为“差”的形式,然后利用平方差公式计算.
(2)当一个三项式进行平方时,常常需通过添括号把其中两项看成一个整体,然后利用完全平方公式计算.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
14.2.2 完全平方公式
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,将完全相同的四张长方形纸片和一张正方形纸片拼成一个较大的正方形,则可得出一个等式为( )
D
A.(a+b) =a +2ab+b
B.(a-b) =a -2ab-b
C. a -b =(a+b)(a-b)
D.(a+b) =(a-b)+4ab
新课精讲
探索新知
1
知识点
添括号法则
运用乘法公式计算,有时要在式子中添括号.在第二章中,我们学过去括号法则,即
a+ ( b + c)=a + b + c;
a -(b +c)=a - b - c.
反过来,就得到添括号法则:
a + b + c = a+ ( b + c);
a - b - c = a -(b +c).
探索新知
也就是说,添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
归 纳
探索新知
例1
(1)下列各式中,成立的是( )
A.-x+y=-(x+y)
B.-3x+8=-3(x+8)
C.2-5x=-(5x-2)
D.-2-5x+y=-(2-5x+y)
C
因为-x+y=-(x-y),所以A选项错误;因为-3x+8=-(3x-8),所以B选项错误;因为2-5x=-(5x-2),所以C选项正确;因为-2-5x+y=-(2+5x-y),所以D选项错误.
导引:
探索新知
(2)下面添括号正确的是( )
A.2a-3b+c- =-(-2a+3b-c+ )
B.x2-2x-y+2x3=-(2x-y)-(-x2-2x3)
C.(a-b)(b-c)(c-a)=[-(a-b)][-(b-c)][-(c-a)]
D.(a-b-c)(a+b-c)=[a-(b-c)][a+(b-c)]
A
导引:
因为2a-3b+c- =-(-2a+3b-c+ ),所以A选项正确;因为x2-2x-y+2x3=-(2x+y)-(-x2-2x3),所以B选项错误;因为(a-b)(b-c)(c-a)=[-(-a+b)][-(-b+c)][-(-c+a)],所以C选项错误;因为(a-b-c)(a+b-c) =[a-(b+c)][a+(b-c)],所以D选项错误.
探索新知
(1)添括号只是一个变形,不改变式子的值.
(2)添括号是否正确,可利用去括号检验.
(3)添括号时,如果括号前面是负号,括到括号里的各项都改变符号,而不是只改变括号里的第一项的符号.
(4)根据题意需要适当地把某几项括到一起,不要随意地乱添加括号.
总 结
典题精讲
1.下列各式添括号正确的是( )
A.-x+y=-(y-x) B.x-y=-(x+y)
C.10-m=5(2-m) D.3-2a=-(2a-3)
D
2.下列添括号正确的是( )
A.a-b+c=a+(b+c) B.m+p-q=m-(p+q)
C.a-b-c+d=a-(b+c-d) D.x2-x+y=-(x2+x-y)
C
探索新知
例2
运用乘法公式计算:
(1)(x + 2y-3)(x - 2y + 3)
解: = [x + (2y-3)][x -(2y-3)]
= x2 - (2y - 3) 2
= x2 -(4y 2 - 12y + 9)
= x2 - 4y 2 + 12y - 9;
探索新知
解:= (a + b ) 2 + 2(a + b )c + c2
= a2 + 2a b + b 2 + 2ac + 2 b c + c2
= a2 + b 2 + c2 + 2a b + 2ac + 2 b c .
有些整式相乘需要先作适当变形,然后再用公式.
(2) (a + b + c)2.
探索新知
本题运用了整体思想求解.对于平方式中底数是三项的多项式,通过添括号将其中任意两项视为一个整体,就符合完全平方公式特点;对于两个乘积式中的三项或四项的多项式,可将符号相同的项及符号相反的项分别添括号视为一个整体,可化成平方差公式的形式,通过平方差公式展开再利用完全平方公式展开,最后合并可得结果.
总 结
典题精讲
1.下列添括号错误的是( )
A.a2-b2-b+a=a2-b2+(a-b)
B.(a+b+c)(a-b-c)=[a+(b+c)][a-(b+c)]
C.a-b+c-d=(a-d)+(c-b)
D.a-b=-(b+a)
D
典题精讲
2.为了应用平方差公式计算(x+3y-1)(x-3y+1),下列变形正确的是( )
A.[x-(3y+1)]2
B.[x+(3y+1)]2
C.[x+(3y-1)] [x-(3y-1)]
D.[(x-3y)+1)] [(x-3y)-1)]
C
学以致用
小试牛刀
1.若(-2x2)(3x2-ax-6)-3x3+x2中不含x的三次项,则a=________.
2.计算:(1)(- ab3)2=________;
(2)4 2 016×(-0.25) 2 017=________;
(3)(π- ) 0=________.
-0.25
1
a2b6
小试牛刀
3.下列计算结果是x2-6x+5的是( )
A.(x-2)(x-3) B.(x-6)(x+1)
C.(x-1)(x-5) D.(x+6)(x-1)
C
4.下列运算正确的是( )
A.x6÷x2=x3 B.x0=1
C.(2x3)2=2x6 D.-2a2 a3=-2a5.
D
小试牛刀
5.下列计算正确的是( )
A.(-x-y)(x+y)=x2-y2
B.(x-y)2=x2-y2
C.(x+3y)(x-3y)=x2-3y2
D.(-x+y)2=x2-2xy+y2
D
小试牛刀
6.计算:
(1)2 0172-2 016×2 018;
原式=2 0172-(2 017-1)×(2 017+1)
=2 0172-(2 0172-12)
=2 0172-2 0172+1
=1.
解:
小试牛刀
(2)
原式=
解:
小试牛刀
(3)1002-992+982-972+…+42-32+22-12.
原式=(1002-992)+(982-972) +…+(22-12)
=(100+99)×(100-99)+(98+97) ×(98-97)+…+(2+1)×(2-1)
=100+99+98+97+…+2+1
=
=5 050.
解:
小试牛刀
7.对任意正整数n,整式(3n+1)(3n-1)- (3-n)(3+n)是不是10的倍
数?为什么?
对任意正整数n,整式(3n+1) (3n-1)-(3-n)
(3+n)是10的倍数,理由如下:(3n+1) (3n-1)
-(3-n)(3+n)=(3n)2-1-(32-n2)=9n2-1-
9+n2=10n2-10=10(n2-1).
∵对任意正整数n,10(n2-1)是10的倍数,
∴(3n+1) (3n-1)-(3-n) (3+n)是10的倍数.
解:
小试牛刀
8.先化简,再求值:2(2x-1)(2x+1)-5x(-x+3y)+4x(-4x- y),
其中x=-1,y=2.
解:
原式=2(4x2-1)+5x2-15xy-16x2-10xy
=8x2-2+5x2-15xy-16x2-10xy
=-3x2-25xy-2.
当x=-1,y=2时,
原式=-3×(-1)2-25×(-1)×2-2=45.
小试牛刀
王老师在一次团体操队列队形设计中,先让全体队员排成一方阵(行与列的人数一样多的队形,且总人数不少于25人),人数正好够用,然后再进行各种队形变化,其中一个队形需分为5人一组,手执彩带变换图形,在讨论分组方案时,有人说现在的队员人数按5人一组分将多出3人,你说这可能吗?
9.
小试牛刀
总人数可能为(5n)2人,(5n+1)2人,(5n+2)2人,(5n+3)2人,(5n+4)2人.(n为正整数) (5n)2=5n 5n;
(5n+1)2=25n2+10n+1=5(5n2+2n)+1;
(5n+2)2=25n2+20n+4=5(5n2+4n)+4;
(5n+3)2=25n2+30n+9=5(5n2+6n+1)+4;
(5n+4)2=25n2+40n+16=5(5n2+8n+3)+1.
由此可见,无论哪一种情况总人数按每组5人分,要么不多出人数,要么多出的人数只可能是1人或4人,不可能是3人.
解:
课堂小结
课堂小结
在乘法公式中添括号的“两种技巧”:
(1)当两个三项式相乘,且它们只含相同项和相反项时,常常需通过添括号把相同项、相反项分别结合,一个化为“和”的形式,一个化为“差”的形式,然后利用平方差公式计算.
(2)当一个三项式进行平方时,常常需通过添括号把其中两项看成一个整体,然后利用完全平方公式计算.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
