人教版(新)八上-15.1.1 从分数到分式【优质课件】
文档属性
| 名称 | 人教版(新)八上-15.1.1 从分数到分式【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 13:52:06 | ||
图片预览











文档简介
(共30张PPT)
15.1.1
从分数到分式
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回忆:什么叫整式 请你举例说明.
整式
单项式: 数与字母或字母与字母的积
多项式: 几个单项式的和
新课精讲
探索新知
1
知识点
分式的定义
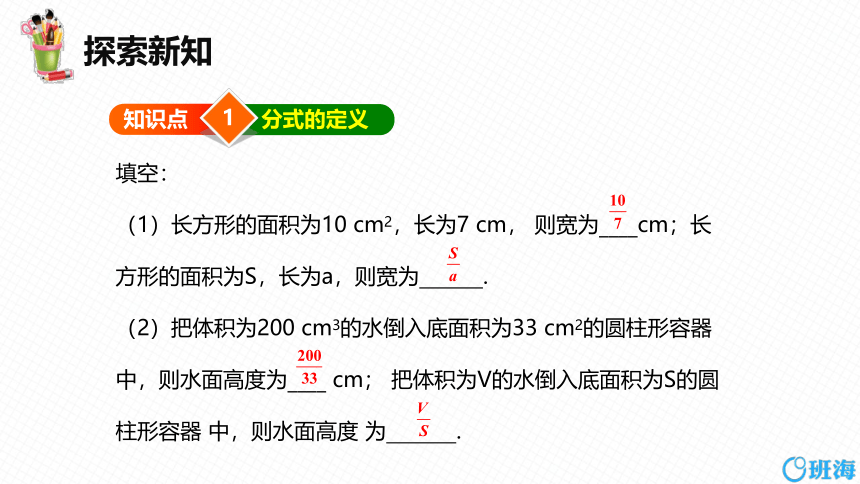
填空:
(1)长方形的面积为10 cm2,长为7 cm, 则宽为____cm;长方形的面积为S,长为a,则宽为 .
(2)把体积为200 cm3的水倒入底面积为33 cm2的圆柱形容器中,则水面高度为____ cm; 把体积为V的水倒入底面积为S的圆柱形容器 中,则水面高度 为 .
探索新知
思考
式子 ,以及式子 有什么共同点?它们与分数有什么相同点和不同点?
都具有分数的形式
相同点
不同点
(观察分母)
分母中有字母
探索新知
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子 叫做分式. 分式 中,A叫做分子,B叫做分母.
定义:
探索新知
下列各式:-3a2, 中,哪些是分式?哪些是整式?
按分式的定义知分母中含有字母的式子是分式,分母中不含有字母的式子是整式.
分式有 ;
整式有 .
例1
导引:
解:
探索新知
判断一个式子是否是分式的方法:首先要具有 的形式,其次A,B是整式,最后看分母是不是含有字母,分母含有字母是判定分式的关键条件.
总 结
典题精讲
1.列式表示下列各量:
(1)某村有n个人,耕地40 hm2,则人均耕地面积为 hm2.
(2)△ABC的面积为S,BC边的长为a, 则高AD为_____.
(3)一辆汽车b h行驶了 a km,则它的平均速度为_____km/h; 一列火车 行驶a km比这辆汽车少用1 h,则它的平均速度为____ km/h.
典题精讲
2.下列式子中,哪些是分式?哪些是整式?两类式子的区别是什么?
分式有:
整式有:
解:
探索新知
2
知识点
分式有意义的条件
思考
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意 义,分式中的分母应满足什么条件?
探索新知
在分式中,当分母的值不为0时,分式有意义;当分母的值为0时,分式无意义.
要点精析:
(1)分母不为0,并不是说分母中的字母不能为0,而是表示分母的整式的值不能为0.
(2)分式是否有意义,只与分式的分母是否为0有关,而与分式的分子的值是否为0无关.
归纳
探索新知
下列分式中的字母满足什么条件时分式有意义?
(1) (2) (3) (4)
例2
解:
(1)要使分式 有意义,则分母3x≠0,即x ≠0.
(2)要使分式 有意义,则分母x-1≠0,即x ≠1.
(3)要使分式 有意义,则分母5-3b≠0,即 ;
(4)要使分式 有意义,则分母x-y≠0,即x≠y.
探索新知
求分式有意义时字母的取值范围,一般是根据分母不等于0构造不等式,求使分式的分母不等于0的字母的取值范围.
总 结
典题精讲
1.使分式 无意义的x满足的条件是( )
A. x=2 B. x=-2
C. x≠2 D. x≠-2
2.下列各式中,无论x取何值,分式都有意义的是( )
A. B. C. D.
B
D
探索新知
3
知识点
分式的值为零的条件
分式值为零的条件及求法:
(1)条件:分子为0,分母不为0.
(2)求法:①利用分子等于0,构建方程.②解方程求出所含字母的值.③代入验证:将所求的值 代入分母,验证是否使分母为0,若分母不为0,所求的值使分式值为0;否则,应舍去.
探索新知
若分式 的值为零,则x的值为( )
A.0 B.1 C.-1 D.±1
例3
导引:
分式的值为0的条件是:分子为0,分母不为0,由此条件
解出x即可.
由x2-1=0,得x=±1.
当x=1时,x-1=0,故x=1不合题意;
当x=-1时,x-1=-2≠0,所以x=-1时分式的值为0.
C
探索新知
求使分式的值为0的字母的值的方法:首先求出使分子的值等于0的字母的值,再检验这个字母的值是否使分母的值等于0,只有当它使分母的值不为0时,才是我们所要求的字母的值.
总 结
学以致用
小试牛刀
1.在代数式 , , , 中, 分式的个数为( )
A.1 B.2
C.3 D.4
2.已知分式的值是零,那么x的值是( )
A.-1 B.0
C.1 D.±1
C
C
小试牛刀
D
小试牛刀
x≠2
1
-3
小试牛刀
8.列式表示下列各量:
(1)王老师骑自行车用了m小时到达距离家n千米的学校,则王老师的平均速度是________千米/小时;若乘公共汽车则可少用0.2小时,则公共汽车的平均速度是________千米/小时;
(2)某班在一次考试中,有m人得90分,有n人得80分,那么这两部分人合在一起的平均分_____________分.
小试牛刀
A
小试牛刀
11.已知当x=-4时,分式 无意义,当x=2时,分式的值为零,求a-b的值.
解:当x=-4时, .
∵分式无意义,∴-4+a=0,∴a=4.
当x=2时, =0,
∴2-b=0,∴b=2.∴a-b=2.
课堂小结
课堂小结
分式的定义
分式有意义
分式的值为0
分母不等于0
①分子=0 ②分母≠0 ③最后答案
整式A、B相除可写为 的形式,若分母中含有字母,那么
叫做分式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
15.1.1
从分数到分式
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回忆:什么叫整式 请你举例说明.
整式
单项式: 数与字母或字母与字母的积
多项式: 几个单项式的和
新课精讲
探索新知
1
知识点
分式的定义
填空:
(1)长方形的面积为10 cm2,长为7 cm, 则宽为____cm;长方形的面积为S,长为a,则宽为 .
(2)把体积为200 cm3的水倒入底面积为33 cm2的圆柱形容器中,则水面高度为____ cm; 把体积为V的水倒入底面积为S的圆柱形容器 中,则水面高度 为 .
探索新知
思考
式子 ,以及式子 有什么共同点?它们与分数有什么相同点和不同点?
都具有分数的形式
相同点
不同点
(观察分母)
分母中有字母
探索新知
一般地,如果A,B表示两个整式,并且B中含有字母,那么式子 叫做分式. 分式 中,A叫做分子,B叫做分母.
定义:
探索新知
下列各式:-3a2, 中,哪些是分式?哪些是整式?
按分式的定义知分母中含有字母的式子是分式,分母中不含有字母的式子是整式.
分式有 ;
整式有 .
例1
导引:
解:
探索新知
判断一个式子是否是分式的方法:首先要具有 的形式,其次A,B是整式,最后看分母是不是含有字母,分母含有字母是判定分式的关键条件.
总 结
典题精讲
1.列式表示下列各量:
(1)某村有n个人,耕地40 hm2,则人均耕地面积为 hm2.
(2)△ABC的面积为S,BC边的长为a, 则高AD为_____.
(3)一辆汽车b h行驶了 a km,则它的平均速度为_____km/h; 一列火车 行驶a km比这辆汽车少用1 h,则它的平均速度为____ km/h.
典题精讲
2.下列式子中,哪些是分式?哪些是整式?两类式子的区别是什么?
分式有:
整式有:
解:
探索新知
2
知识点
分式有意义的条件
思考
我们知道,要使分数有意义,分数中的分母不能为0.要使分式有意 义,分式中的分母应满足什么条件?
探索新知
在分式中,当分母的值不为0时,分式有意义;当分母的值为0时,分式无意义.
要点精析:
(1)分母不为0,并不是说分母中的字母不能为0,而是表示分母的整式的值不能为0.
(2)分式是否有意义,只与分式的分母是否为0有关,而与分式的分子的值是否为0无关.
归纳
探索新知
下列分式中的字母满足什么条件时分式有意义?
(1) (2) (3) (4)
例2
解:
(1)要使分式 有意义,则分母3x≠0,即x ≠0.
(2)要使分式 有意义,则分母x-1≠0,即x ≠1.
(3)要使分式 有意义,则分母5-3b≠0,即 ;
(4)要使分式 有意义,则分母x-y≠0,即x≠y.
探索新知
求分式有意义时字母的取值范围,一般是根据分母不等于0构造不等式,求使分式的分母不等于0的字母的取值范围.
总 结
典题精讲
1.使分式 无意义的x满足的条件是( )
A. x=2 B. x=-2
C. x≠2 D. x≠-2
2.下列各式中,无论x取何值,分式都有意义的是( )
A. B. C. D.
B
D
探索新知
3
知识点
分式的值为零的条件
分式值为零的条件及求法:
(1)条件:分子为0,分母不为0.
(2)求法:①利用分子等于0,构建方程.②解方程求出所含字母的值.③代入验证:将所求的值 代入分母,验证是否使分母为0,若分母不为0,所求的值使分式值为0;否则,应舍去.
探索新知
若分式 的值为零,则x的值为( )
A.0 B.1 C.-1 D.±1
例3
导引:
分式的值为0的条件是:分子为0,分母不为0,由此条件
解出x即可.
由x2-1=0,得x=±1.
当x=1时,x-1=0,故x=1不合题意;
当x=-1时,x-1=-2≠0,所以x=-1时分式的值为0.
C
探索新知
求使分式的值为0的字母的值的方法:首先求出使分子的值等于0的字母的值,再检验这个字母的值是否使分母的值等于0,只有当它使分母的值不为0时,才是我们所要求的字母的值.
总 结
学以致用
小试牛刀
1.在代数式 , , , 中, 分式的个数为( )
A.1 B.2
C.3 D.4
2.已知分式的值是零,那么x的值是( )
A.-1 B.0
C.1 D.±1
C
C
小试牛刀
D
小试牛刀
x≠2
1
-3
小试牛刀
8.列式表示下列各量:
(1)王老师骑自行车用了m小时到达距离家n千米的学校,则王老师的平均速度是________千米/小时;若乘公共汽车则可少用0.2小时,则公共汽车的平均速度是________千米/小时;
(2)某班在一次考试中,有m人得90分,有n人得80分,那么这两部分人合在一起的平均分_____________分.
小试牛刀
A
小试牛刀
11.已知当x=-4时,分式 无意义,当x=2时,分式的值为零,求a-b的值.
解:当x=-4时, .
∵分式无意义,∴-4+a=0,∴a=4.
当x=2时, =0,
∴2-b=0,∴b=2.∴a-b=2.
课堂小结
课堂小结
分式的定义
分式有意义
分式的值为0
分母不等于0
①分子=0 ②分母≠0 ③最后答案
整式A、B相除可写为 的形式,若分母中含有字母,那么
叫做分式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
