人教版(新)八上-15.2.2 分式的加减 第三课时【优质课件】
文档属性
| 名称 | 人教版(新)八上-15.2.2 分式的加减 第三课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览






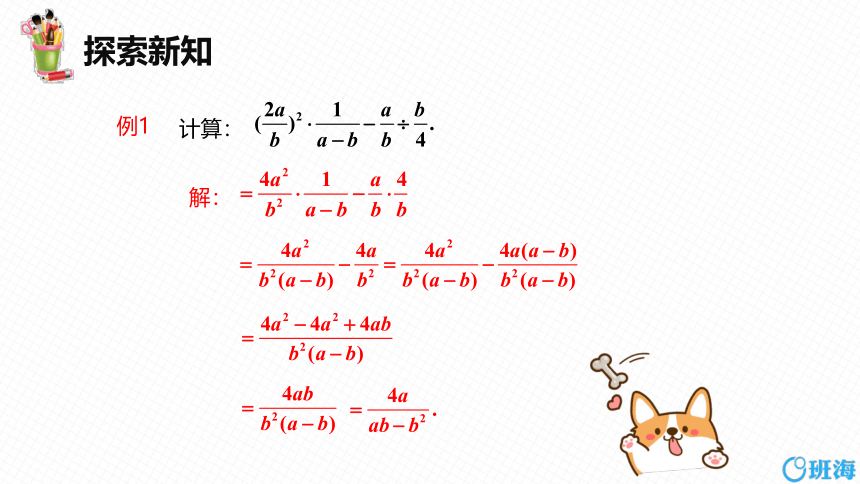





文档简介
(共30张PPT)
15.2.2 分式的加减
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
1. 只含某一级运算:从左到右依次运算.
2. 有不同级运算在一起的:从高级到低级运算先算乘方三级;再算乘除二级;最后算加减一级.
3. 带有括号的运算:从内到外依次进行运算先算小括号; 再算中括号; 最后算大括号里面的.
有理数和整式的混合运算法则:
新课精讲
探索新知
1
知识点
分式的混合运算
分式的加、减、乘、除、乘方的混合运算顺序原则:
优先进行乘方运算,其次进行乘、除运算,最后进行加、减运算;如果有括号,则优先进行括号内的运算.
对于同级运算,则按照从左到右的顺序,依次进行.
探索新知
计算:
例1
解:
探索新知
式与数有相同的混合运算顺序:先乘方,再乘除,然后加减.
总 结
探索新知
例2
计算:
导引:对于(1)先计算除法,再计算减法;对于
解:
探索新知
导引:对于(2) 先计算乘方,再计算乘法,最后计算减法;
解:
探索新知
导引:对于(3)把除法转化为乘法后,可运用分配律计算,也可以先将括号内的分式通分,再把分式除法转化为乘法进行计算.
解:
探索新知
在进行分式的混合运算时,应先算乘方,再算乘除,最后算加减,有括号的要先算括号里面的.
总 结
典题精讲
1.下列等式成立的是( )
A.
B.
C.
D.
C
典题精讲
3.计算 的结果是( )
A. 2 B. C. D. -2
2.计算 的结果是( )
A. B.
C. D.
C
A
探索新知
2
知识点
分式的混合运算的应用
例3
先化简,再求值: 其中,a满足
a-2=0.
导引:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,将a的值代入计算即可求出值.
探索新知
解:
当a-2=0,即a=2时,原式=3.
典题精讲
1.先化简,再求值: 其中
2.若 则W=( )
A. a+2(a≠-2) B. -a+2(a≠2)
C. a-2(a≠2) D. -a-2(a≠±2)
解:
D
典题精讲
3.已知实数a,b,c满足a+b=ab=c,有下列结论:
①若c≠0,则 ②若a=3,则b+c=9;
③若a=b=c,则abc=0;
④若a,b,c中只有两个数相等,则a+b+c=8.
其中正确的是__________(把所有正确结论的序号都选上).
① ③ ④
学以致用
小试牛刀
1.同分母分式相加减,分母_____,把分子________,即 =______.
不变
相加减
2.异分母分式相加减,先_____,变为________的分式,再加减,即 =______±______=______.
通分
同分母
3.某厂有煤x t,原计划每天用煤a t,由于采用新的节约措施,实际每天用煤为原计划的 ,则实际比原计划可多用____天.
小试牛刀
B
5.计算 的结果是( )
A. B. C. -1 D.1
B
小试牛刀
C
B
小试牛刀
小试牛刀
(1)该学生解答过程是从第____步开始出错的,其错误原因是_____________________;
(2)请写出此题正确的解答过程.
一
分式的基本性质用错
小试牛刀
小试牛刀
10.计算.
解:原式=
解:原式=
·(x+4)(x-4)
=(x- 4) -x(x+4)
=-12x+16
小试牛刀
(1)A=(x-3)· -1= -1= = ;
11. 已知A=(x-3)÷ -1
(1)化简A;
(2)若x满足不等式组 ,且x为整数时,求A的值.
(x+2)(x2-6x+9)
x2-4
(x+2)(x-2)
(x+2)(x-3)2
x-2
x-3
x-2-x+3
x-3
1
x-3
1
3
4
3
②
x
3
<
2x-11-
(2)
由①得:x<1,由②得:x>-1,
∴不等式组的解集为-1解:
课堂小结
课堂小结
1.分式混合运算的步骤:先乘方,再乘除,最后加减,有括号先算括号里面的.
2.分式混合运算常出现的错误:
(1)运算顺序易错;
(2)符号变换易错;
(3)错用分配律,只有乘法才有分配律;
(4)忽视分数线的括号作用;
(5)运算的结果不是最简分式或整式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
15.2.2 分式的加减
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
1. 只含某一级运算:从左到右依次运算.
2. 有不同级运算在一起的:从高级到低级运算先算乘方三级;再算乘除二级;最后算加减一级.
3. 带有括号的运算:从内到外依次进行运算先算小括号; 再算中括号; 最后算大括号里面的.
有理数和整式的混合运算法则:
新课精讲
探索新知
1
知识点
分式的混合运算
分式的加、减、乘、除、乘方的混合运算顺序原则:
优先进行乘方运算,其次进行乘、除运算,最后进行加、减运算;如果有括号,则优先进行括号内的运算.
对于同级运算,则按照从左到右的顺序,依次进行.
探索新知
计算:
例1
解:
探索新知
式与数有相同的混合运算顺序:先乘方,再乘除,然后加减.
总 结
探索新知
例2
计算:
导引:对于(1)先计算除法,再计算减法;对于
解:
探索新知
导引:对于(2) 先计算乘方,再计算乘法,最后计算减法;
解:
探索新知
导引:对于(3)把除法转化为乘法后,可运用分配律计算,也可以先将括号内的分式通分,再把分式除法转化为乘法进行计算.
解:
探索新知
在进行分式的混合运算时,应先算乘方,再算乘除,最后算加减,有括号的要先算括号里面的.
总 结
典题精讲
1.下列等式成立的是( )
A.
B.
C.
D.
C
典题精讲
3.计算 的结果是( )
A. 2 B. C. D. -2
2.计算 的结果是( )
A. B.
C. D.
C
A
探索新知
2
知识点
分式的混合运算的应用
例3
先化简,再求值: 其中,a满足
a-2=0.
导引:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,将a的值代入计算即可求出值.
探索新知
解:
当a-2=0,即a=2时,原式=3.
典题精讲
1.先化简,再求值: 其中
2.若 则W=( )
A. a+2(a≠-2) B. -a+2(a≠2)
C. a-2(a≠2) D. -a-2(a≠±2)
解:
D
典题精讲
3.已知实数a,b,c满足a+b=ab=c,有下列结论:
①若c≠0,则 ②若a=3,则b+c=9;
③若a=b=c,则abc=0;
④若a,b,c中只有两个数相等,则a+b+c=8.
其中正确的是__________(把所有正确结论的序号都选上).
① ③ ④
学以致用
小试牛刀
1.同分母分式相加减,分母_____,把分子________,即 =______.
不变
相加减
2.异分母分式相加减,先_____,变为________的分式,再加减,即 =______±______=______.
通分
同分母
3.某厂有煤x t,原计划每天用煤a t,由于采用新的节约措施,实际每天用煤为原计划的 ,则实际比原计划可多用____天.
小试牛刀
B
5.计算 的结果是( )
A. B. C. -1 D.1
B
小试牛刀
C
B
小试牛刀
小试牛刀
(1)该学生解答过程是从第____步开始出错的,其错误原因是_____________________;
(2)请写出此题正确的解答过程.
一
分式的基本性质用错
小试牛刀
小试牛刀
10.计算.
解:原式=
解:原式=
·(x+4)(x-4)
=(x- 4) -x(x+4)
=-12x+16
小试牛刀
(1)A=(x-3)· -1= -1= = ;
11. 已知A=(x-3)÷ -1
(1)化简A;
(2)若x满足不等式组 ,且x为整数时,求A的值.
(x+2)(x2-6x+9)
x2-4
(x+2)(x-2)
(x+2)(x-3)2
x-2
x-3
x-2-x+3
x-3
1
x-3
1
3
4
3
②
x
3
<
2x-1
(2)
由①得:x<1,由②得:x>-1,
∴不等式组的解集为-1
课堂小结
课堂小结
1.分式混合运算的步骤:先乘方,再乘除,最后加减,有括号先算括号里面的.
2.分式混合运算常出现的错误:
(1)运算顺序易错;
(2)符号变换易错;
(3)错用分配律,只有乘法才有分配律;
(4)忽视分数线的括号作用;
(5)运算的结果不是最简分式或整式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
