人教版(新)八上-11.1.1 三角形的边【优质课件】
文档属性
| 名称 | 人教版(新)八上-11.1.1 三角形的边【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
11.1.1 三角形的边
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面请同学们仔细观察一组图片,找出你熟悉的几何图形.
你能画出一个三角形吗?
新课精讲
探索新知
1
知识点
三角形及有关概念
下面哪个是三角形?
什么是三角形?
结合你画的三角形,说明三角形是由什么组成的.
探索新知
A
B
C
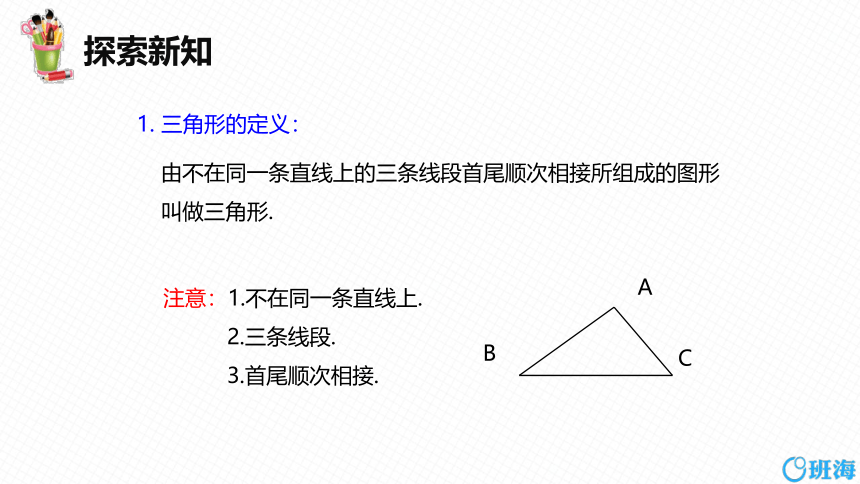
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
注意:1.不在同一条直线上.
2.三条线段.
3.首尾顺次相接.
1. 三角形的定义:
探索新知
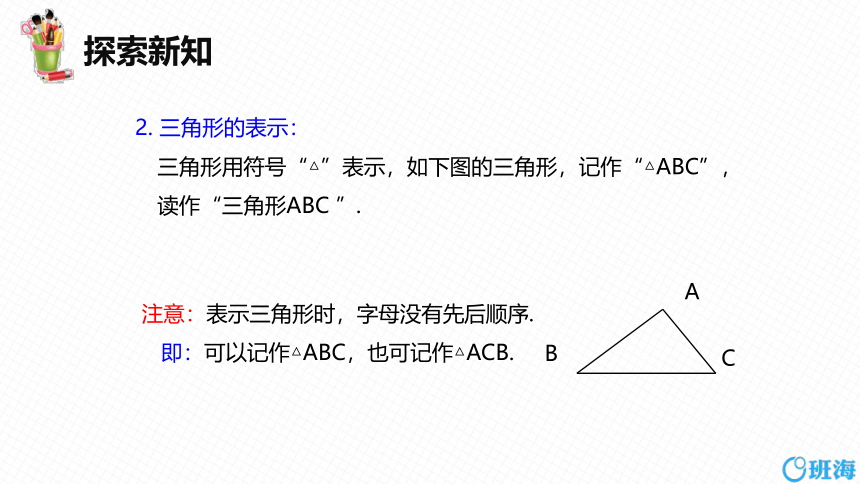
注意:表示三角形时,字母没有先后顺序.
即:可以记作△ABC,也可记作△ACB.
2. 三角形的表示:
三角形用符号“△”表示,如下图的三角形,记作“△ABC”,读作“三角形ABC ”.
A
B
C
探索新知
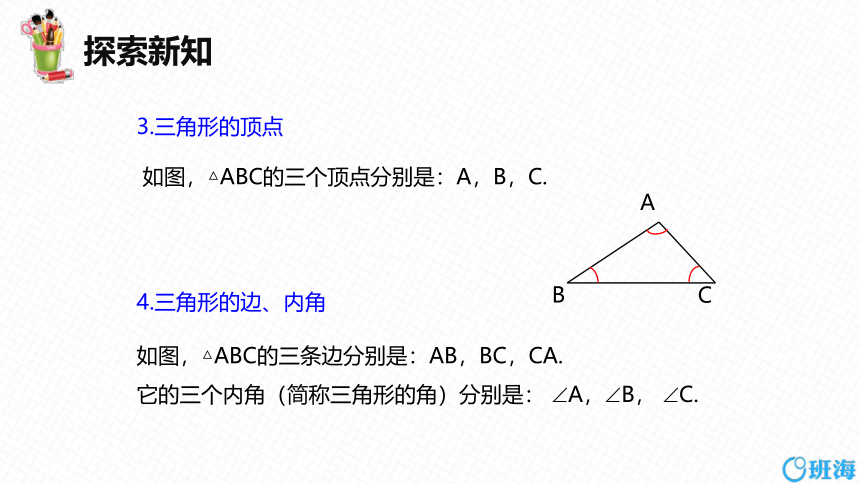
如图,△ABC的三个顶点分别是:A,B,C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB,BC,CA.
它的三个内角(简称三角形的角)分别是: A, B, C.
A
B
C
4.三角形的边、内角
探索新知
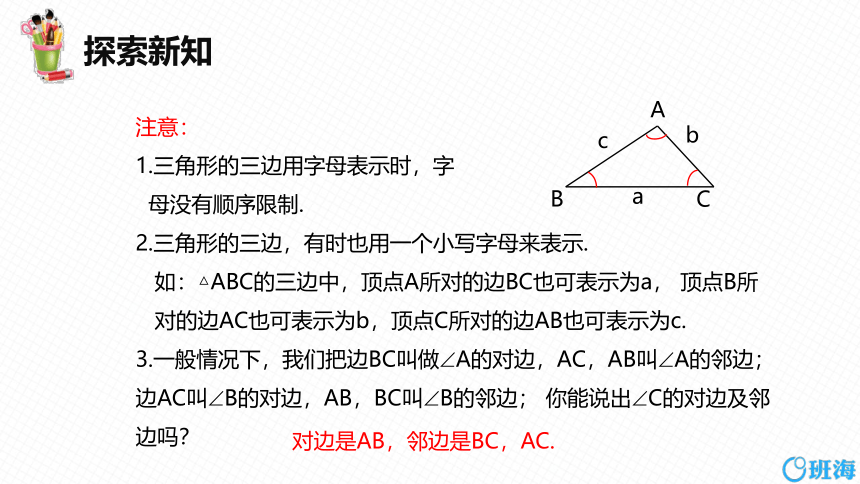
注意:
1.三角形的三边用字母表示时,字
母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a, 顶点B所
对的边AC也可表示为b,顶点C所对的边AB也可表示为c.
3.一般情况下,我们把边BC叫做 A的对边,AC,AB叫 A的邻边;边AC叫 B的对边,AB,BC叫 B的邻边; 你能说出 C的对边及邻边吗?
a
b
c
A
B
C
对边是AB,邻边是BC,AC.
典题精讲
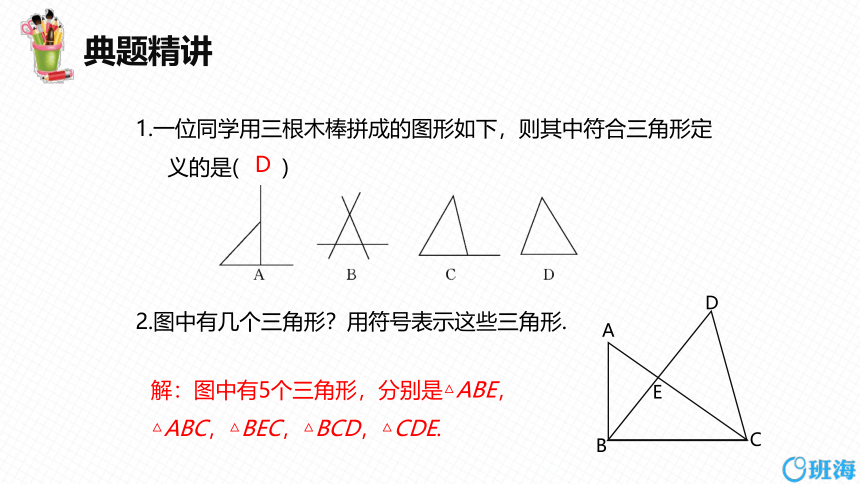
1.一位同学用三根木棒拼成的图形如下,则其中符合三角形定
义的是( )
D
2.图中有几个三角形?用符号表示这些三角形.
解:图中有5个三角形,分别是△ABE,△ABC,△BEC,△BCD,△CDE.
A
B
C
D
E
典题精讲
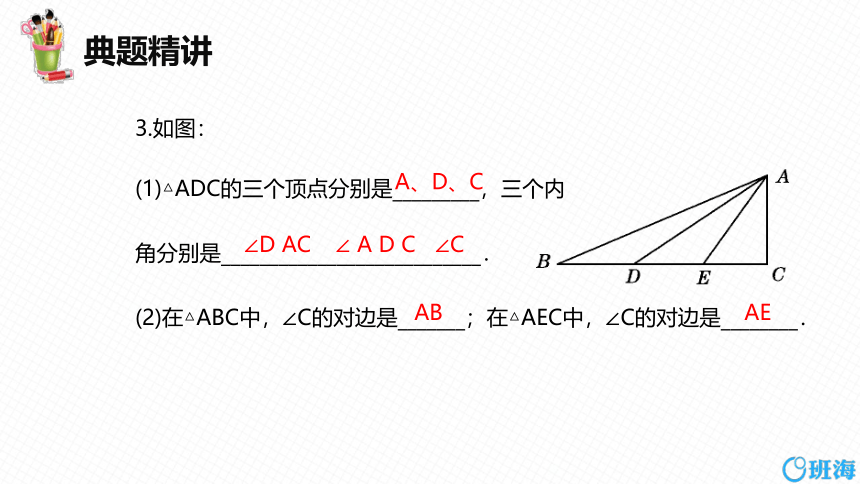
3.如图:
(1)△ADC的三个顶点分别是_________,三个内
角分别是___________________________.
(2)在△ABC中,∠C的对边是_______;在△AEC中,∠C的对边是________.
A、D、C
∠C
∠D AC
∠ A D C
AB
AE
探索新知
2
知识点
三角形的分类
我们知道,按照三个内角的大小,可以将三角形分为锐角三角形、直 角三角形和钝角三角形. 如何按照边的关系对三角形进行分类呢?说说你的想法,并与同学交流.
探索新知
我们知道:
三边都相等的三角形叫做等边三角形(图(1));
有两条边相等的三角形叫做等腰三角形(图(2) ).
图 (3)中的三角形是三边都不相等的三角形.
(3)
(2)
(1)
A
A
A
C
C
C
B
B
B
探索新知
我们还知道:在等腰三角形中,相等的两边都叫做腰,另一边叫做底边, 两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
B
C
顶角
底角
底角
腰
腰
底边
探索新知
等边三角形是特殊的等腰三角形,即底边和腰
相等的等腰三角形.
以“是否有边相等”,可以将三角形分为两类:
三边都不相等的三角形和等腰三角形.
探索新知
总 结
三角形
按
角
分
锐角三角形
直角三角形
钝角三角形
按
边
分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等
的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
典题精讲
1.下列说法:其中正确的有( )
①等边三角形是等腰三角形;
②等腰三角形也可能是直角三角形;
③三角形按边分类可分为等腰三角形、等边三角形和三边都不相
等的三角形;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.1个 B.2个 C.3个 D.4个
C
典题精讲
2.已知一个三角形是等腰三角形,则这个三角形( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形、直角三角形或钝角三角形
D
探索新知
3
知识点
三角形的三边关系
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
探索新知
如图三角形中,假设有一只小虫要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
探索新知
对于任意一个△ ABC,如果把其中任意两个顶点 (例如B,C)看成定点,由“两点之间,线段最短”可得
AB+AC>BC. ①
同理有
AC+BC>AB, ②
AB+BC>AC. ③
一般地,我们有三角形两边的和大于第三边.
由不等式②③移项可得BC>AB-AC,BC>AC-AB.
这就是说,三角形两边的差小于第三边.
探索新知
例1 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm.
x+2x+2x = 18.
解得x = 3. 6.
所以,三边长分别为3. 6 cm,7.2 cm,7.2 cm.
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
探索新知
如果4 cm长的边为底边,设腰长为x cm,则 4+2x = 18.
解得x = 7.
如果4 cm长的边为腰,设底边长为 x cm,则
2×4+x = 18.
解得x = 10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不
能围成腰长 是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
探索新知
注意:
1.一个三角形的三边关系可以归纳成如下一句话:三角形的任何两边之和大于第三边,任何两边之差小于第三边.
2.在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边.
总 结
典题精讲
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3, 4, 8; (2) 5, 6, 11; (3) 5, 6, 10.
解:(1)不能组成三角形.
因为3+4<8,不满足三角形的三边关系.
(2)不能组成三角形.
因为5+6=11,不满足三角形的三边关系.
(3)能组成三角形.
因为5+6>10,满足三角形的三边关系.
典题精讲
2.已知三角形两边的长分别是4和10,则此三角形第三边的长
可能是( )
A.5 B.6 C.12 D.16
3.下列长度的三条线段能组成三角形的是( )
A.5,6,10 B.5,6,11
C.3,4,8 D.4a,4a,8a(a>0)
C
A
学以致用
小试牛刀
1.已知线段AB,BC,CA组成的图形如图所示,此图形为三角形,则三角形具有的结构特征为:
(1)由不在同一条直线上的________条线段组成;
三
(2)三条线段首尾________相接,其中三条边是线段_______________,
三个顶点是点___________,三个内角是___________________ .
此三角形记作________,读作“____________”.
顺次
AB,BC,CA
A,B,C
∠A,∠B,∠C
△ABC
三角形ABC
小试牛刀
(1)以AC为边的三角形有______个,是________________________;
(2)∠BCE是△_______和△______的内角;
(3)在△ACE中,∠CAE的对边是_____.
2.如图,在△ABC中,D是BC边上一点,E是AD上一点.
3
△ACE,△ACD,△ACB
BCE
DCE
CE
小试牛刀
3.(1)三角形按角分类可分为______三角形、_____三角形和
_____三角形;
(2)三角形按边可分为三边都不相等的三角形和等腰三角
形两类,等腰三角形又可分为__________________的等
腰三角形和________三角形.
锐角
直角
钝角
底边和腰不相等
等边
4.如图,在△ABC中,因为“两点之间,线段最
短”,所以AB+AC_____BC,BC+AC_____AB.
因此,有BC+AC_____AB_____BC-AC.这就是
说,三角形两边的和_______第三边,两边的差
________第三边.
>
>
>
>
大于
小于
小试牛刀
5.下列说法正确的是( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两条边相等.
A.①②③ B.②③ C.①③ D.③
D
小试牛刀
6.如图所示的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
D
小试牛刀
7.长度分别为2,7,x的三条线段能组成一个三角形,x的值
可以是( )
A.4 B.5
C.6 D.9
C
8.若一个三角形的两边长分别为2和4,则该三角形的周长可
能是( )
A.6 B.7
C.11 D.12
C
小试牛刀
9.已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,
且a为方程|x-4|=2的解.求△ABC的周长,并判断△ABC的形状.
解:由(b-2)2+|c-3|=0,(b-2)2≥0,|c-3|≥0,
得b-2=0,c-3=0,则b=2,c=3.
解|x-4|=2,得x=6或2.
当a=6时,2+3<6,所以a=6不合题意,舍去;
当a=2时,满足三角形三边关系,△ABC的周长为2+2+3=7,△ABC是等腰三角形.
小试牛刀
10.已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.
求证AC+BD> (AB+BC+CD+DA).
证明:在△OAB中,有OA+OB>AB;
在△OAD中,有________________;
在△ODC中,有__________________;
OA+OD>AD
OD+OC>CD
在△________中,有__________________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+BC+CD+DA,
即________________________________.
∴AC+BD> (AB+BC+CD+DA).
OBC
OB+OC>BC
2(AC+BD)>AB+BC+CD+DA
课堂小结
课堂小结
通过本课时的学习需要我们掌握
三角形
表示方法
概念
分类
三边关系
1.三条线段
2.不在同一直线上
3.首尾顺次相接
△ABC
按“边”分
按“角”分
两边之和大于第三边,两边之差小于第三边
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
11.1.1 三角形的边
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
下面请同学们仔细观察一组图片,找出你熟悉的几何图形.
你能画出一个三角形吗?
新课精讲
探索新知
1
知识点
三角形及有关概念
下面哪个是三角形?
什么是三角形?
结合你画的三角形,说明三角形是由什么组成的.
探索新知
A
B
C
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
注意:1.不在同一条直线上.
2.三条线段.
3.首尾顺次相接.
1. 三角形的定义:
探索新知
注意:表示三角形时,字母没有先后顺序.
即:可以记作△ABC,也可记作△ACB.
2. 三角形的表示:
三角形用符号“△”表示,如下图的三角形,记作“△ABC”,读作“三角形ABC ”.
A
B
C
探索新知
如图,△ABC的三个顶点分别是:A,B,C.
3.三角形的顶点
如图,△ABC的三条边分别是:AB,BC,CA.
它的三个内角(简称三角形的角)分别是: A, B, C.
A
B
C
4.三角形的边、内角
探索新知
注意:
1.三角形的三边用字母表示时,字
母没有顺序限制.
2.三角形的三边,有时也用一个小写字母来表示.
如:△ABC的三边中,顶点A所对的边BC也可表示为a, 顶点B所
对的边AC也可表示为b,顶点C所对的边AB也可表示为c.
3.一般情况下,我们把边BC叫做 A的对边,AC,AB叫 A的邻边;边AC叫 B的对边,AB,BC叫 B的邻边; 你能说出 C的对边及邻边吗?
a
b
c
A
B
C
对边是AB,邻边是BC,AC.
典题精讲
1.一位同学用三根木棒拼成的图形如下,则其中符合三角形定
义的是( )
D
2.图中有几个三角形?用符号表示这些三角形.
解:图中有5个三角形,分别是△ABE,△ABC,△BEC,△BCD,△CDE.
A
B
C
D
E
典题精讲
3.如图:
(1)△ADC的三个顶点分别是_________,三个内
角分别是___________________________.
(2)在△ABC中,∠C的对边是_______;在△AEC中,∠C的对边是________.
A、D、C
∠C
∠D AC
∠ A D C
AB
AE
探索新知
2
知识点
三角形的分类
我们知道,按照三个内角的大小,可以将三角形分为锐角三角形、直 角三角形和钝角三角形. 如何按照边的关系对三角形进行分类呢?说说你的想法,并与同学交流.
探索新知
我们知道:
三边都相等的三角形叫做等边三角形(图(1));
有两条边相等的三角形叫做等腰三角形(图(2) ).
图 (3)中的三角形是三边都不相等的三角形.
(3)
(2)
(1)
A
A
A
C
C
C
B
B
B
探索新知
我们还知道:在等腰三角形中,相等的两边都叫做腰,另一边叫做底边, 两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
B
C
顶角
底角
底角
腰
腰
底边
探索新知
等边三角形是特殊的等腰三角形,即底边和腰
相等的等腰三角形.
以“是否有边相等”,可以将三角形分为两类:
三边都不相等的三角形和等腰三角形.
探索新知
总 结
三角形
按
角
分
锐角三角形
直角三角形
钝角三角形
按
边
分
三边都不相等的三角形
三角形的分类
等腰三角形
底边和腰不相等
的等腰三角形
等边三角形
三边都不相等的三角形
等腰三角形
等边三角形
典题精讲
1.下列说法:其中正确的有( )
①等边三角形是等腰三角形;
②等腰三角形也可能是直角三角形;
③三角形按边分类可分为等腰三角形、等边三角形和三边都不相
等的三角形;
④三角形按角分类应分为锐角三角形、直角三角形和钝角三角形.
A.1个 B.2个 C.3个 D.4个
C
典题精讲
2.已知一个三角形是等腰三角形,则这个三角形( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形、直角三角形或钝角三角形
D
探索新知
3
知识点
三角形的三边关系
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?能证明你的结论吗?
探索新知
如图三角形中,假设有一只小虫要从点B出发沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
探索新知
对于任意一个△ ABC,如果把其中任意两个顶点 (例如B,C)看成定点,由“两点之间,线段最短”可得
AB+AC>BC. ①
同理有
AC+BC>AB, ②
AB+BC>AC. ③
一般地,我们有三角形两边的和大于第三边.
由不等式②③移项可得BC>AB-AC,BC>AC-AB.
这就是说,三角形两边的差小于第三边.
探索新知
例1 用一条长为18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4 cm的等腰三角形吗?为什么?
解:(1)设底边长为x cm,则腰长为2x cm.
x+2x+2x = 18.
解得x = 3. 6.
所以,三边长分别为3. 6 cm,7.2 cm,7.2 cm.
(2)因为长为4 cm的边可能是腰,也可能是底边,所以需要分情况讨论.
探索新知
如果4 cm长的边为底边,设腰长为x cm,则 4+2x = 18.
解得x = 7.
如果4 cm长的边为腰,设底边长为 x cm,则
2×4+x = 18.
解得x = 10.
因为4+4<10,不符合三角形两边的和大于第三边,所以不
能围成腰长 是4 cm的等腰三角形.
由以上讨论可知,可以围成底边长是4 cm的等腰三角形.
探索新知
注意:
1.一个三角形的三边关系可以归纳成如下一句话:三角形的任何两边之和大于第三边,任何两边之差小于第三边.
2.在做题时,不仅要考虑到两边之和大于第三边,还必须考虑到两边之差小于第三边.
总 结
典题精讲
1.下列长度的三条线段能否组成三角形?为什么?
(1) 3, 4, 8; (2) 5, 6, 11; (3) 5, 6, 10.
解:(1)不能组成三角形.
因为3+4<8,不满足三角形的三边关系.
(2)不能组成三角形.
因为5+6=11,不满足三角形的三边关系.
(3)能组成三角形.
因为5+6>10,满足三角形的三边关系.
典题精讲
2.已知三角形两边的长分别是4和10,则此三角形第三边的长
可能是( )
A.5 B.6 C.12 D.16
3.下列长度的三条线段能组成三角形的是( )
A.5,6,10 B.5,6,11
C.3,4,8 D.4a,4a,8a(a>0)
C
A
学以致用
小试牛刀
1.已知线段AB,BC,CA组成的图形如图所示,此图形为三角形,则三角形具有的结构特征为:
(1)由不在同一条直线上的________条线段组成;
三
(2)三条线段首尾________相接,其中三条边是线段_______________,
三个顶点是点___________,三个内角是___________________ .
此三角形记作________,读作“____________”.
顺次
AB,BC,CA
A,B,C
∠A,∠B,∠C
△ABC
三角形ABC
小试牛刀
(1)以AC为边的三角形有______个,是________________________;
(2)∠BCE是△_______和△______的内角;
(3)在△ACE中,∠CAE的对边是_____.
2.如图,在△ABC中,D是BC边上一点,E是AD上一点.
3
△ACE,△ACD,△ACB
BCE
DCE
CE
小试牛刀
3.(1)三角形按角分类可分为______三角形、_____三角形和
_____三角形;
(2)三角形按边可分为三边都不相等的三角形和等腰三角
形两类,等腰三角形又可分为__________________的等
腰三角形和________三角形.
锐角
直角
钝角
底边和腰不相等
等边
4.如图,在△ABC中,因为“两点之间,线段最
短”,所以AB+AC_____BC,BC+AC_____AB.
因此,有BC+AC_____AB_____BC-AC.这就是
说,三角形两边的和_______第三边,两边的差
________第三边.
>
>
>
>
大于
小于
小试牛刀
5.下列说法正确的是( )
①等腰三角形是等边三角形;
②三角形按边分类可分为等腰三角形、等边三角形和不等边三角形;
③等腰三角形至少有两条边相等.
A.①②③ B.②③ C.①③ D.③
D
小试牛刀
6.如图所示的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
D
小试牛刀
7.长度分别为2,7,x的三条线段能组成一个三角形,x的值
可以是( )
A.4 B.5
C.6 D.9
C
8.若一个三角形的两边长分别为2和4,则该三角形的周长可
能是( )
A.6 B.7
C.11 D.12
C
小试牛刀
9.已知a,b,c为△ABC的三边长,b,c满足(b-2)2+|c-3|=0,
且a为方程|x-4|=2的解.求△ABC的周长,并判断△ABC的形状.
解:由(b-2)2+|c-3|=0,(b-2)2≥0,|c-3|≥0,
得b-2=0,c-3=0,则b=2,c=3.
解|x-4|=2,得x=6或2.
当a=6时,2+3<6,所以a=6不合题意,舍去;
当a=2时,满足三角形三边关系,△ABC的周长为2+2+3=7,△ABC是等腰三角形.
小试牛刀
10.已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.
求证AC+BD> (AB+BC+CD+DA).
证明:在△OAB中,有OA+OB>AB;
在△OAD中,有________________;
在△ODC中,有__________________;
OA+OD>AD
OD+OC>CD
在△________中,有__________________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+BC+CD+DA,
即________________________________.
∴AC+BD> (AB+BC+CD+DA).
OBC
OB+OC>BC
2(AC+BD)>AB+BC+CD+DA
课堂小结
课堂小结
通过本课时的学习需要我们掌握
三角形
表示方法
概念
分类
三边关系
1.三条线段
2.不在同一直线上
3.首尾顺次相接
△ABC
按“边”分
按“角”分
两边之和大于第三边,两边之差小于第三边
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
