人教版(新)八上-11.1.2 三角形的高、中线与角平分线【优质课件】
文档属性
| 名称 | 人教版(新)八上-11.1.2 三角形的高、中线与角平分线【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览







文档简介
(共37张PPT)
11.1.2 三角形的
高、中线与角平分线
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
垂线的定义:
线段中点的定义:
当两条直线相交所成的四个角巾,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
把一条线段分成两条相等的线段的点.
角平分线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
新课精讲
探索新知
1
知识点
三角形的高
你能过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
你还记得 “过一点画已知直线的垂线” 吗
探索新知
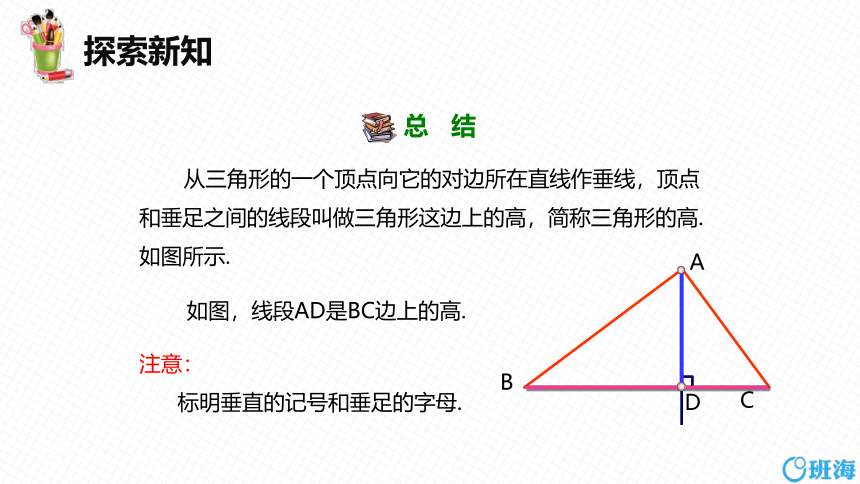
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高. 如图所示.
A
B
C
D
如图,线段AD是BC边上的高.
注意:
标明垂直的记号和垂足的字母.
总 结
探索新知
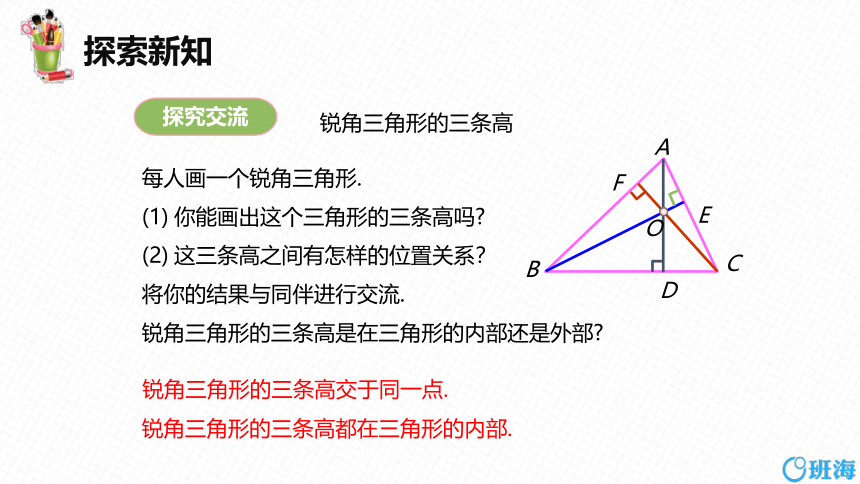
锐角三角形的三条高
每人画一个锐角三角形.
你能画出这个三角形的三条高吗
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高是在三角形的内部还是外部
O
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
探究交流
探索新知
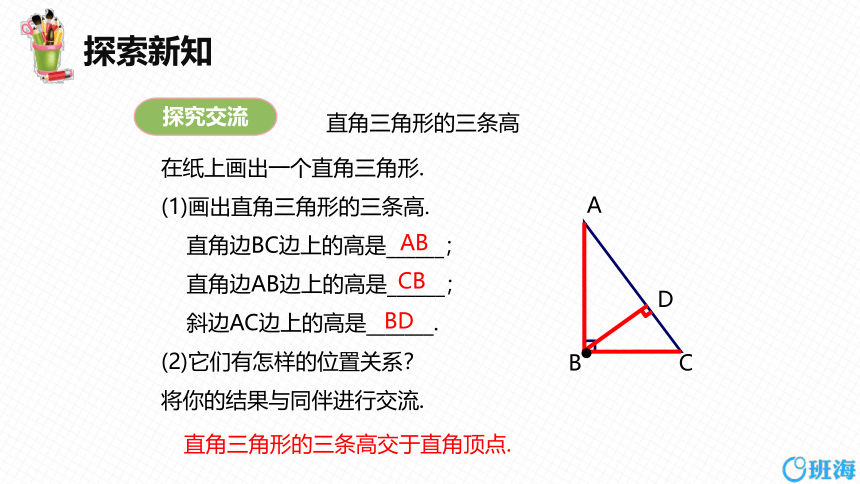
直角三角形的三条高
在纸上画出一个直角三角形.
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
直角边AB边上的高是______;
斜边AC边上的高是_______.
(2)它们有怎样的位置关系?
将你的结果与同伴进行交流.
A
B
C
AB
CB
D
BD
●
直角三角形的三条高交于直角顶点.
探究交流
探索新知
A
B
C
D
E
F
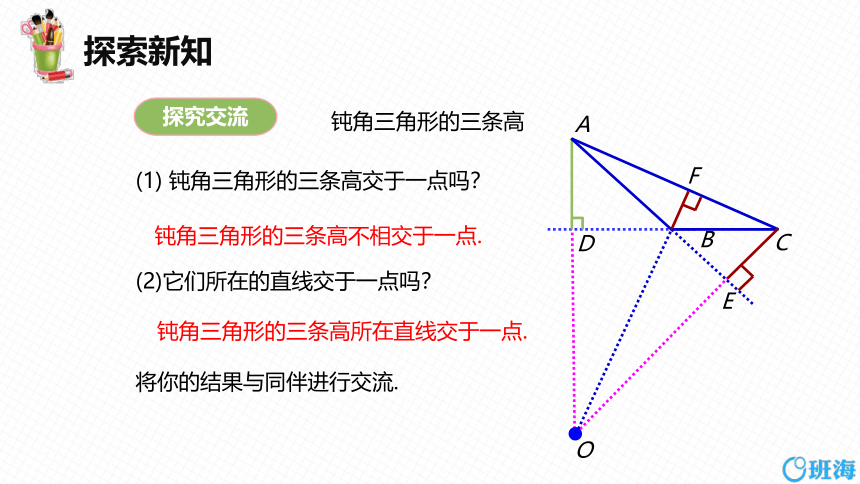
钝角三角形的三条高
(1) 钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
O
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
探究交流
探索新知
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高.
总 结
探索新知
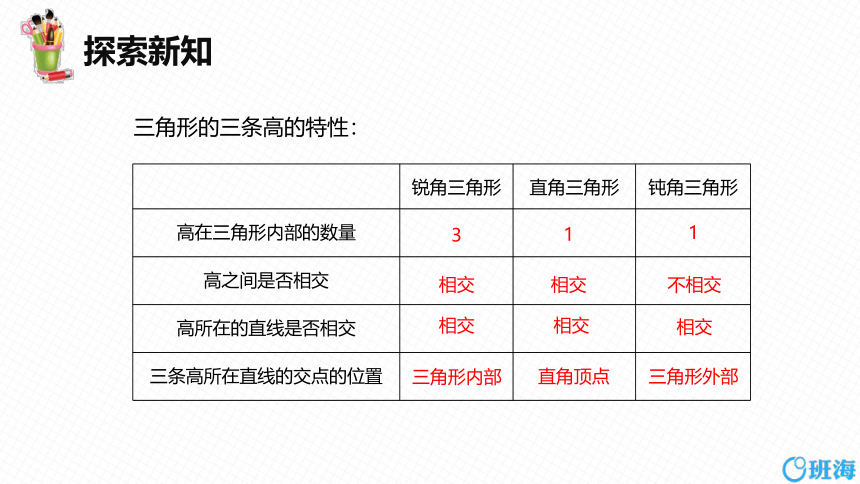
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
三角形的三条高的特性:
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
典题精讲
1.如图,(1) (2)和(3)中的三个∠B有什么不同?这三条△ABC的边
BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?
解:
(1)中的∠B是锐角,高AD在△ABC内部.
(2)中的∠B是直角,高AD与边AB重合.
(3)中的∠B是钝角,高AD的垂足在CB
的延长线上, 即高AD在△ABC的外部.
规律:当∠C是锐角时,如果∠B是锐角,高AD在△ABC的内部;
如果∠B是直角,高AD与边AB重合;如果∠B是钝角,高AD的
垂足在CB的延长线上,即高AD在△ABC的外部.
典题精讲
2.在直角三角形中,有两条高是它的________,另一条高在这个
三角形的________.锐角三角形的三条高的交点在______________,
直角三角形的三条高的交点在_______________________,钝角三
角形的三条高所在直线的交点在_________________.
直角边
内部
三角形的内部
三角形的外部
两直角边的交点处
探索新知
2
知识点
三角形的中线
如图 (1),连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
用同样方法,你能画出△ABC的另两条边上的中线吗?
A
B
C
D
(1)
探索新知
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线.
总 结
探索新知
如图 (2),三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
A
B
C
D
(2)
E
F
探索新知
例1 在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12 cm和15 cm两部分,求△ABC的各边长.
导引:因为中线BD将△ABC的周长分成两部分:(BC+CD)和(AD+AB),无法确定谁为12 cm,谁为15 cm,故应分类讨论;另外题中涉及线段较多,因此可建立方程的模型,利用设未知数来求解.
探索新知
解:设AB=x cm,则AD=CD= x cm.
(1)如图①,若AB+AD=12 cm,则x+ x=12.解得x=8,
即AB=AC=8 cm,则CD=4 cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8 cm,8 cm,11 cm.
(2)如图②,若AB+AD=15 cm,则x+ x=15.
解得x=10,即AB=AC=10 cm,则CD=5 cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10 cm,10 cm,7 cm.
综上所述,△ABC的三边长分别为8 cm,8 cm,11 cm或10 cm,
10 cm,7 cm.
典题精讲
1. 如图(1),AD,BE,CF是△ABC的三条中线,则
AB= 2 ________,BD=____,AE= ____.
AD或BF
CD
AC
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
B
典题精讲
3.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和
△BCD的周长的差是( )
A.2
B.3
C.6
D.不能确定
A
探索新知
3
知识点
三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线?
探索新知
A
B
C
D
任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
︶
︶
1
2
三角形的三条角平分线相交于一点,交点在三角形的内部.
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD = ∠BAC.
探索新知
A
C
B
F
E
D
O
因为BE是△ABC的角平分线,所以______=________= _______.因为
CF是△ABC的角平分线,所以∠ACB=2_______=2__________.
∠ABE
∠CBE
∠ABC
∠ACF
∠BCF
探索新知
1.三角形的角平分线与角的平分线的区别是:
三角形的角平分线是线段,而角的平分线是一条射线;
它们的联系是都是平分角。
2.三角形的角平分线判别的“两种方法”
(1)看该线段是否分三角形的内角为相等的两部分.
(2)看线段的两个端点,其中一个端点是三角形的顶点,另一个端点要落在对边上.
总 结
典题精讲
如图(2),AD,BE,CF是△ ABC的三条角平分线,则
∠1=______,∠3= _______,∠ACB= 2_______.
∠2
∠ABC
∠4
学以致用
小试牛刀
1.从三角形的一个顶点向它所对的边所在直线画 ______ ,顶点和
_____间的线段叫做三角形的高.锐角三角形的三条高在三角形
的______ ;直角三角形的高,有两条在___________,另一条在
___________;钝角三角形的高,有两条在___________,另一条
在______________.三角形三条高______________都交于一点.
垂线
垂足
内部
直角边上
三角形内部
三角形外部
三角形内部
所在直线
2.三角形的角平分线是三角形一个角的平分线与对边相交,这个
角的顶点与交点之间的_______.它区别于角的平分线在于它是
________,而角的平分线是________.
线段
线段
射线
小试牛刀
3.在三角形中,连接一个_____和它___________的________,所得
______叫做三角形的中线;三角形的一条中线把原三角形分成
________相等的两部分;三角形的三条中线________于一点,这
个点叫做三角形的________.
顶点
所对的边
中点
线段
面积
相交
重心
4.若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
A
小试牛刀
5.如图,在△ABC中,D,E两点分别在AB,BC上,若 AD∶DB
=CE∶EB=2∶3,则△DBE与△ADC的面积比为( )
A.3∶5
B.4∶5
C.9∶10
D.15∶16
C
小试牛刀
6.如图,D,E分别是△ABC的边AC,BC的中点,下列结论中不
正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
D
小试牛刀
7.如图,在△ABC中,AD⊥BC,BE⊥AC,
BC=13,AC=10,AD=8.求BE的长.
解:∵AD⊥BC,BE⊥AC,∴S△ABC= BC AD= AC BE.
∵AD=8,AC=10,BC=13,∴13×8=10BE.∴BE=10.4.
小试牛刀
8.如图,已知△ABC的周长为21cm,
AB=6cm,BC边上的中线AD=5cm,
△ABD的周长为15 cm.求AC的长.
解:∵AB=6 cm,AD=5 cm,△ABD的周长为15 cm,
∴BD=15-6-5=4(cm).
∵AD是BC边上的中线,∴BC=2BD=8 cm.
∵△ABC的周长为21 cm,∴AC=21-6-8=7(cm).
小试牛刀
9.如图,AD是△ABC的角平分线,DE∥AC交AB
于E,∠1=∠2,则DF与AB有什么位置关系?
并说明理由.
解:DF∥AB.理由如下:
∵DE∥AC,∴∠1=∠4.
∵AD是△ABC的角平分线,∴∠3=∠4,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.∴DF∥AB.
课堂小结
课堂小结
1.三角形的高、中线、角平分线等有关概念及
它们的画法.
2.三角形的高、中线、角平分线几何表达及简
单应用.
今天我们学了什么呢?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
11.1.2 三角形的
高、中线与角平分线
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
垂线的定义:
线段中点的定义:
当两条直线相交所成的四个角巾,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
把一条线段分成两条相等的线段的点.
角平分线的定义:
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
新课精讲
探索新知
1
知识点
三角形的高
你能过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
你还记得 “过一点画已知直线的垂线” 吗
探索新知
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高. 如图所示.
A
B
C
D
如图,线段AD是BC边上的高.
注意:
标明垂直的记号和垂足的字母.
总 结
探索新知
锐角三角形的三条高
每人画一个锐角三角形.
你能画出这个三角形的三条高吗
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
锐角三角形的三条高是在三角形的内部还是外部
O
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
探究交流
探索新知
直角三角形的三条高
在纸上画出一个直角三角形.
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
直角边AB边上的高是______;
斜边AC边上的高是_______.
(2)它们有怎样的位置关系?
将你的结果与同伴进行交流.
A
B
C
AB
CB
D
BD
●
直角三角形的三条高交于直角顶点.
探究交流
探索新知
A
B
C
D
E
F
钝角三角形的三条高
(1) 钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
O
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
探究交流
探索新知
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高.
总 结
探索新知
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
三角形的三条高的特性:
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
典题精讲
1.如图,(1) (2)和(3)中的三个∠B有什么不同?这三条△ABC的边
BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?
解:
(1)中的∠B是锐角,高AD在△ABC内部.
(2)中的∠B是直角,高AD与边AB重合.
(3)中的∠B是钝角,高AD的垂足在CB
的延长线上, 即高AD在△ABC的外部.
规律:当∠C是锐角时,如果∠B是锐角,高AD在△ABC的内部;
如果∠B是直角,高AD与边AB重合;如果∠B是钝角,高AD的
垂足在CB的延长线上,即高AD在△ABC的外部.
典题精讲
2.在直角三角形中,有两条高是它的________,另一条高在这个
三角形的________.锐角三角形的三条高的交点在______________,
直角三角形的三条高的交点在_______________________,钝角三
角形的三条高所在直线的交点在_________________.
直角边
内部
三角形的内部
三角形的外部
两直角边的交点处
探索新知
2
知识点
三角形的中线
如图 (1),连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
用同样方法,你能画出△ABC的另两条边上的中线吗?
A
B
C
D
(1)
探索新知
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线.
总 结
探索新知
如图 (2),三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
A
B
C
D
(2)
E
F
探索新知
例1 在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12 cm和15 cm两部分,求△ABC的各边长.
导引:因为中线BD将△ABC的周长分成两部分:(BC+CD)和(AD+AB),无法确定谁为12 cm,谁为15 cm,故应分类讨论;另外题中涉及线段较多,因此可建立方程的模型,利用设未知数来求解.
探索新知
解:设AB=x cm,则AD=CD= x cm.
(1)如图①,若AB+AD=12 cm,则x+ x=12.解得x=8,
即AB=AC=8 cm,则CD=4 cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8 cm,8 cm,11 cm.
(2)如图②,若AB+AD=15 cm,则x+ x=15.
解得x=10,即AB=AC=10 cm,则CD=5 cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10 cm,10 cm,7 cm.
综上所述,△ABC的三边长分别为8 cm,8 cm,11 cm或10 cm,
10 cm,7 cm.
典题精讲
1. 如图(1),AD,BE,CF是△ABC的三条中线,则
AB= 2 ________,BD=____,AE= ____.
AD或BF
CD
AC
2.三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
B
典题精讲
3.如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和
△BCD的周长的差是( )
A.2
B.3
C.6
D.不能确定
A
探索新知
3
知识点
三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线?
探索新知
A
B
C
D
任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么
●
●
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
︶
︶
1
2
三角形的三条角平分线相交于一点,交点在三角形的内部.
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD = ∠BAC.
探索新知
A
C
B
F
E
D
O
因为BE是△ABC的角平分线,所以______=________= _______.因为
CF是△ABC的角平分线,所以∠ACB=2_______=2__________.
∠ABE
∠CBE
∠ABC
∠ACF
∠BCF
探索新知
1.三角形的角平分线与角的平分线的区别是:
三角形的角平分线是线段,而角的平分线是一条射线;
它们的联系是都是平分角。
2.三角形的角平分线判别的“两种方法”
(1)看该线段是否分三角形的内角为相等的两部分.
(2)看线段的两个端点,其中一个端点是三角形的顶点,另一个端点要落在对边上.
总 结
典题精讲
如图(2),AD,BE,CF是△ ABC的三条角平分线,则
∠1=______,∠3= _______,∠ACB= 2_______.
∠2
∠ABC
∠4
学以致用
小试牛刀
1.从三角形的一个顶点向它所对的边所在直线画 ______ ,顶点和
_____间的线段叫做三角形的高.锐角三角形的三条高在三角形
的______ ;直角三角形的高,有两条在___________,另一条在
___________;钝角三角形的高,有两条在___________,另一条
在______________.三角形三条高______________都交于一点.
垂线
垂足
内部
直角边上
三角形内部
三角形外部
三角形内部
所在直线
2.三角形的角平分线是三角形一个角的平分线与对边相交,这个
角的顶点与交点之间的_______.它区别于角的平分线在于它是
________,而角的平分线是________.
线段
线段
射线
小试牛刀
3.在三角形中,连接一个_____和它___________的________,所得
______叫做三角形的中线;三角形的一条中线把原三角形分成
________相等的两部分;三角形的三条中线________于一点,这
个点叫做三角形的________.
顶点
所对的边
中点
线段
面积
相交
重心
4.若AD是△ABC的中线,则下列结论中错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
A
小试牛刀
5.如图,在△ABC中,D,E两点分别在AB,BC上,若 AD∶DB
=CE∶EB=2∶3,则△DBE与△ADC的面积比为( )
A.3∶5
B.4∶5
C.9∶10
D.15∶16
C
小试牛刀
6.如图,D,E分别是△ABC的边AC,BC的中点,下列结论中不
正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
D
小试牛刀
7.如图,在△ABC中,AD⊥BC,BE⊥AC,
BC=13,AC=10,AD=8.求BE的长.
解:∵AD⊥BC,BE⊥AC,∴S△ABC= BC AD= AC BE.
∵AD=8,AC=10,BC=13,∴13×8=10BE.∴BE=10.4.
小试牛刀
8.如图,已知△ABC的周长为21cm,
AB=6cm,BC边上的中线AD=5cm,
△ABD的周长为15 cm.求AC的长.
解:∵AB=6 cm,AD=5 cm,△ABD的周长为15 cm,
∴BD=15-6-5=4(cm).
∵AD是BC边上的中线,∴BC=2BD=8 cm.
∵△ABC的周长为21 cm,∴AC=21-6-8=7(cm).
小试牛刀
9.如图,AD是△ABC的角平分线,DE∥AC交AB
于E,∠1=∠2,则DF与AB有什么位置关系?
并说明理由.
解:DF∥AB.理由如下:
∵DE∥AC,∴∠1=∠4.
∵AD是△ABC的角平分线,∴∠3=∠4,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3.∴DF∥AB.
课堂小结
课堂小结
1.三角形的高、中线、角平分线等有关概念及
它们的画法.
2.三角形的高、中线、角平分线几何表达及简
单应用.
今天我们学了什么呢?
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
