人教版(新)八上-11.3.1 多边形【优质课件】
文档属性
| 名称 | 人教版(新)八上-11.3.1 多边形【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览










文档简介
(共38张PPT)
11.3.1 多边形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
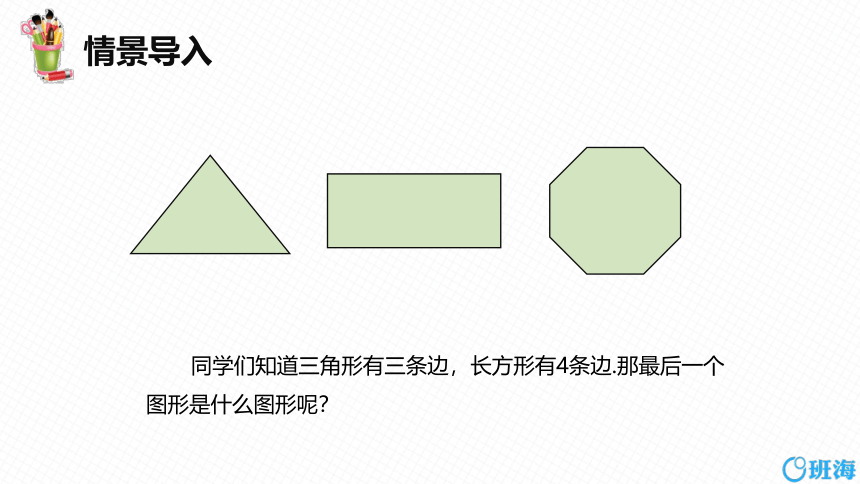
同学们知道三角形有三条边,长方形有4条边.那最后一个图形是什么图形呢?
新课精讲
探索新知
1
知识点
多边形
观察图中的图片,其中的房屋结构、蜂巢结构等给我们以
由一些线段 围成的图形的形象,你能从图中想象出几个由一些
线段围成的图形吗?
探索新知
多边形定义
平面内,不在同一条直线上的几条线段首尾顺次相接,所得到的封闭图形叫多边形.
多边形以边数命名:
五边形ABCDE或五边形EDCBA
A
B
C
D
E
A
B
C
D
E
F
探索新知
多边形按组成它的线段的条数分成三角形、 四边形、五边形……三角形是最简单的多边形.如果一个多边形由n条线段组成,那么这个多边形就叫做n边形.如图,螺母底面的边缘可以设计为六边形,也可以设计为八边形.
探索新知
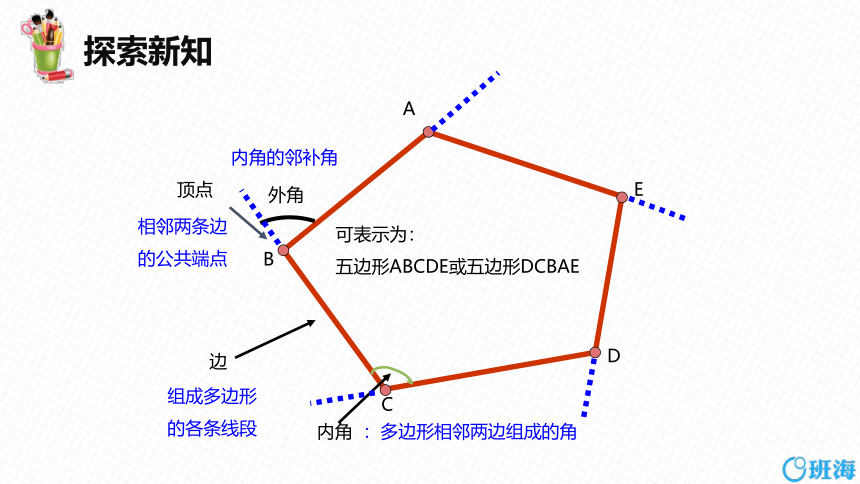
顶点
内角
边
可表示为:
五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
组成多边形的各条线段
相邻两条边的公共端点
探索新知
下列说法中,正确的有( )
(1)三角形是边数最少的多边形;
(2)由n条线段连接起来组成的图形叫多边形;
(3)n边形有n条边、n个顶点、2n个内角和外角;
(4)多边形分为凹多边形和凸多边形.
A.1个 B.2个 C.3个 D.4个
(2)的说法不严密,应点明三点:其一,“不在同一直线上”的线段;其二,是“平面图形”;其三,“线段首尾顺次连接”;(3)n边形有n个内角和2n个外角,即外角的个数是内角个数的2倍.(1)(4)说法正确.
例1
导引:
B
探索新知
理解多边形的定义需注意:
(1)线段必须“不在同一直线上”且条数要不少于3条;
(2)必须是“平面图形”;
(3)首尾顺次相接.
总 结
典题精讲
1.对于多边形的外角,最准确的表述是( )
A.内角的邻角
B.与内角有公共顶点的角
C.内角的邻补角
D.内角的对顶角
C
典题精讲
2.图中的各个图形,是否是多边形?如果是,说出是几边形.
解:图①②④是多边形,图③不是多边形.其中图①是四边形,图②是五边形,图④是五边形.
探索新知
2
知识点
多边形的对角线
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
A
C
B
D
E
三角形有几条对角线?
探索新知
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
探索新知
你能写出每个图形中对角线的总条数吗?如果不能,请画出所有对角线.
0
2
5
9
太难画了!
探索新知
你能告诉我二十边形的对角线的总条数吗?五十边形呢?一百边形呢?n边形呢?
探索新知
边数 3 4 5 6 7 … n
从一个顶点出发 的对角线的条数 …
总的对角线条数 …
上述对角线分成 的三角形个数 …
0
0
0
1
2
2
2
5
3
3
9
4
4
14
5
n-3
n-2
n(n-3)
2
总 结
典题精讲
1.画出下列多边形的全部对角线:
四边形的一条对角线将四边形分成几个三角形?从五边形的一个顶点出发,可 以画出几条对角线?它们将五边形分成几个三角形?
解:两个三角形;两条对角线;将五边形分成三个三角形.
典题精讲
2.在凸多边形中,四边形有2条对角线,五边形有5条对角线,
观察探索凸十边形的对角线有( )
A.29条
B.32条
C.35条
D.38条
C
探索新知
3
知识点
正多边形
正五边形
正六边形
正八边形
各边相等,各内角也相等的多边形叫做正多边形.
等边三角形
(正三角形)
正方形
(正四边形)
探索新知
紧扣正多边形的概念识别:
(1)等腰三角形的底边与腰不一定相等,所以不一定是正多边形;
(2)等边三角形三条边都相等,三个角都相等,是正多边形;
(3)长方形的四个角相等,但长与宽不一定相等,所以不一定是
正多边形.
(4)正方形的四条边相等,四个角相等,是正多边形.
下列说法:(1)等腰三角形是正多边形;(2)等边三角形是正多边形;(3)长方形是正多边形;(4)正方形是正多边形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
例2
导引:
B
探索新知
对于正多边形的识别,各条边都相等,各个
角都相等,这两个条件缺一不可.
总 结
典题精讲
1.下列属于正多边形的有( )
①等边三角形; ②长方形; ③正方形;
④梯形; ⑤圆
A.1个 B.2个 C.3个 D.4个
B
典题精讲
2.下列说法中不正确的是( )
A.正多边形的各边都相等
B.各边都相等的多边形是正多边形
C.正三角形就是等边三角形
D.六条边、六个内角都相等的六边形都是正六边形
3.“菱形是正多边形”这句话是否正确?为什么?
B
解:不正确.因为菱形不一定是正多边形,菱 形的四条边
相等,但四个角不一定相等.
学以致用
小试牛刀
1.在________内,由一些线段________顺次相接组成的封闭图形
叫做多边形.
多边形具有两个特征:
(1)在____________内;
(2)由一些线段______,且这些线段______顺次相接.
平面
首尾
同一平面
组成
首尾
2.一个正多边形必须同时具备各个角________且各条边________;若一个正多边形的周长是100,边长为10,则此正多边形是正________边形.
都相等
都相等
十
小试牛刀
3.下列图形中,不是多边形的是( )
C
4.如图所示的四边形的表示方法正确的是( )
A.四边形ABCD
B.四边形ACBD
C.四边形ABDC
D.四边形ADBC
C
小试牛刀
5.多边形的对角线是指( )
A.连接多边形任意两个顶点的线段
B.连接多边形相邻的两个顶点的线段
C.连接多边形不相邻的两个顶点的线段
D.连接多边形不相邻的两个顶点的线段的长
C
小试牛刀
6.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,
那么打开以后的形状是( )
A.六边形
B.八边形
C.十二边形
D.十六边形
C
小试牛刀
7.如图,把边长为12的正三角形纸板剪去三个小正三角形,
得到正六边形,则剪去的小正三角形的边长为( )
A.1
B.2
C.3
D.4
D
小试牛刀
8.下列属于正多边形的特征的有( )
①各边相等; ②各个内角相等;
③各个外角相等; ④各条对角线都相等;
⑤从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个
C.4个 D.5个
B
小试牛刀
9.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,
OD,可以得到几个三角形?得到的三角形个数与边数有何
关系?
解:可以得到4个三角形,得到的三角
形个数与边数相等.
小试牛刀
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?得到的三角形个数与边数有何关系?
可以得到4个三角形,得到的三角形个数为边数减1.
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?得到的三角形个数与边数有何关系?
可以得到4个三角形,得到的三角形个数为边数减2.
课堂小结
课堂小结
平面内,不在同一条直线上的几条线段首尾顺次相接,所得到的封闭图形叫多边形.各条边都相等的多边形叫做正多边形.
与三角形类似地,多边形相邻两边组成的角叫做多边形的内角,如图中的∠A、∠B、∠C、∠D、∠E.多边形的边与它的邻边的延长线组成的角叫做多边形的外角.如图中的∠1是五边形ABCDE的一个外角.
连接多边形的不相邻的两个顶点的线段,叫做多边形的对角线.
n边形有n(n-3)/2条对角线.
课堂小结
在图(1)中,画出四边形ABCD的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的四边形叫做凸四边形,这样的多边形称为凸多边形;而图(2)就不满足上述凸多边形的特征,因为我们画BD所在直线,整个多边形不都在这条直线的同一侧,我们称它为凹多边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
11.3.1 多边形
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
同学们知道三角形有三条边,长方形有4条边.那最后一个图形是什么图形呢?
新课精讲
探索新知
1
知识点
多边形
观察图中的图片,其中的房屋结构、蜂巢结构等给我们以
由一些线段 围成的图形的形象,你能从图中想象出几个由一些
线段围成的图形吗?
探索新知
多边形定义
平面内,不在同一条直线上的几条线段首尾顺次相接,所得到的封闭图形叫多边形.
多边形以边数命名:
五边形ABCDE或五边形EDCBA
A
B
C
D
E
A
B
C
D
E
F
探索新知
多边形按组成它的线段的条数分成三角形、 四边形、五边形……三角形是最简单的多边形.如果一个多边形由n条线段组成,那么这个多边形就叫做n边形.如图,螺母底面的边缘可以设计为六边形,也可以设计为八边形.
探索新知
顶点
内角
边
可表示为:
五边形ABCDE或五边形DCBAE
A
B
C
D
E
外角
:多边形相邻两边组成的角
内角的邻补角
组成多边形的各条线段
相邻两条边的公共端点
探索新知
下列说法中,正确的有( )
(1)三角形是边数最少的多边形;
(2)由n条线段连接起来组成的图形叫多边形;
(3)n边形有n条边、n个顶点、2n个内角和外角;
(4)多边形分为凹多边形和凸多边形.
A.1个 B.2个 C.3个 D.4个
(2)的说法不严密,应点明三点:其一,“不在同一直线上”的线段;其二,是“平面图形”;其三,“线段首尾顺次连接”;(3)n边形有n个内角和2n个外角,即外角的个数是内角个数的2倍.(1)(4)说法正确.
例1
导引:
B
探索新知
理解多边形的定义需注意:
(1)线段必须“不在同一直线上”且条数要不少于3条;
(2)必须是“平面图形”;
(3)首尾顺次相接.
总 结
典题精讲
1.对于多边形的外角,最准确的表述是( )
A.内角的邻角
B.与内角有公共顶点的角
C.内角的邻补角
D.内角的对顶角
C
典题精讲
2.图中的各个图形,是否是多边形?如果是,说出是几边形.
解:图①②④是多边形,图③不是多边形.其中图①是四边形,图②是五边形,图④是五边形.
探索新知
2
知识点
多边形的对角线
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
A
C
B
D
E
三角形有几条对角线?
探索新知
画出多边形中从一个顶点出发的对角线,写出它的条数.
0
1
2
3
5
从n边形的一个顶点出发能画出多少条对角线?
探索新知
你能写出每个图形中对角线的总条数吗?如果不能,请画出所有对角线.
0
2
5
9
太难画了!
探索新知
你能告诉我二十边形的对角线的总条数吗?五十边形呢?一百边形呢?n边形呢?
探索新知
边数 3 4 5 6 7 … n
从一个顶点出发 的对角线的条数 …
总的对角线条数 …
上述对角线分成 的三角形个数 …
0
0
0
1
2
2
2
5
3
3
9
4
4
14
5
n-3
n-2
n(n-3)
2
总 结
典题精讲
1.画出下列多边形的全部对角线:
四边形的一条对角线将四边形分成几个三角形?从五边形的一个顶点出发,可 以画出几条对角线?它们将五边形分成几个三角形?
解:两个三角形;两条对角线;将五边形分成三个三角形.
典题精讲
2.在凸多边形中,四边形有2条对角线,五边形有5条对角线,
观察探索凸十边形的对角线有( )
A.29条
B.32条
C.35条
D.38条
C
探索新知
3
知识点
正多边形
正五边形
正六边形
正八边形
各边相等,各内角也相等的多边形叫做正多边形.
等边三角形
(正三角形)
正方形
(正四边形)
探索新知
紧扣正多边形的概念识别:
(1)等腰三角形的底边与腰不一定相等,所以不一定是正多边形;
(2)等边三角形三条边都相等,三个角都相等,是正多边形;
(3)长方形的四个角相等,但长与宽不一定相等,所以不一定是
正多边形.
(4)正方形的四条边相等,四个角相等,是正多边形.
下列说法:(1)等腰三角形是正多边形;(2)等边三角形是正多边形;(3)长方形是正多边形;(4)正方形是正多边形.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
例2
导引:
B
探索新知
对于正多边形的识别,各条边都相等,各个
角都相等,这两个条件缺一不可.
总 结
典题精讲
1.下列属于正多边形的有( )
①等边三角形; ②长方形; ③正方形;
④梯形; ⑤圆
A.1个 B.2个 C.3个 D.4个
B
典题精讲
2.下列说法中不正确的是( )
A.正多边形的各边都相等
B.各边都相等的多边形是正多边形
C.正三角形就是等边三角形
D.六条边、六个内角都相等的六边形都是正六边形
3.“菱形是正多边形”这句话是否正确?为什么?
B
解:不正确.因为菱形不一定是正多边形,菱 形的四条边
相等,但四个角不一定相等.
学以致用
小试牛刀
1.在________内,由一些线段________顺次相接组成的封闭图形
叫做多边形.
多边形具有两个特征:
(1)在____________内;
(2)由一些线段______,且这些线段______顺次相接.
平面
首尾
同一平面
组成
首尾
2.一个正多边形必须同时具备各个角________且各条边________;若一个正多边形的周长是100,边长为10,则此正多边形是正________边形.
都相等
都相等
十
小试牛刀
3.下列图形中,不是多边形的是( )
C
4.如图所示的四边形的表示方法正确的是( )
A.四边形ABCD
B.四边形ACBD
C.四边形ABDC
D.四边形ADBC
C
小试牛刀
5.多边形的对角线是指( )
A.连接多边形任意两个顶点的线段
B.连接多边形相邻的两个顶点的线段
C.连接多边形不相邻的两个顶点的线段
D.连接多边形不相邻的两个顶点的线段的长
C
小试牛刀
6.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,
那么打开以后的形状是( )
A.六边形
B.八边形
C.十二边形
D.十六边形
C
小试牛刀
7.如图,把边长为12的正三角形纸板剪去三个小正三角形,
得到正六边形,则剪去的小正三角形的边长为( )
A.1
B.2
C.3
D.4
D
小试牛刀
8.下列属于正多边形的特征的有( )
①各边相等; ②各个内角相等;
③各个外角相等; ④各条对角线都相等;
⑤从一个顶点引出的对角线将正n边形分成面积相等的(n-2)个三角形.
A.2个 B.3个
C.4个 D.5个
B
小试牛刀
9.(1)如图①,O为四边形ABCD内一点,连接OA,OB,OC,
OD,可以得到几个三角形?得到的三角形个数与边数有何
关系?
解:可以得到4个三角形,得到的三角
形个数与边数相等.
小试牛刀
(2)如图②,点O在五边形ABCDE的AB边上,连接OC,OD,OE,可以得到几个三角形?得到的三角形个数与边数有何关系?
可以得到4个三角形,得到的三角形个数为边数减1.
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?得到的三角形个数与边数有何关系?
可以得到4个三角形,得到的三角形个数为边数减2.
课堂小结
课堂小结
平面内,不在同一条直线上的几条线段首尾顺次相接,所得到的封闭图形叫多边形.各条边都相等的多边形叫做正多边形.
与三角形类似地,多边形相邻两边组成的角叫做多边形的内角,如图中的∠A、∠B、∠C、∠D、∠E.多边形的边与它的邻边的延长线组成的角叫做多边形的外角.如图中的∠1是五边形ABCDE的一个外角.
连接多边形的不相邻的两个顶点的线段,叫做多边形的对角线.
n边形有n(n-3)/2条对角线.
课堂小结
在图(1)中,画出四边形ABCD的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的四边形叫做凸四边形,这样的多边形称为凸多边形;而图(2)就不满足上述凸多边形的特征,因为我们画BD所在直线,整个多边形不都在这条直线的同一侧,我们称它为凹多边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
