人教版(新)八上-11.3.2 多边形的内角和【优质课件】
文档属性
| 名称 | 人教版(新)八上-11.3.2 多边形的内角和【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
11.3.2 多边形
的内角和
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
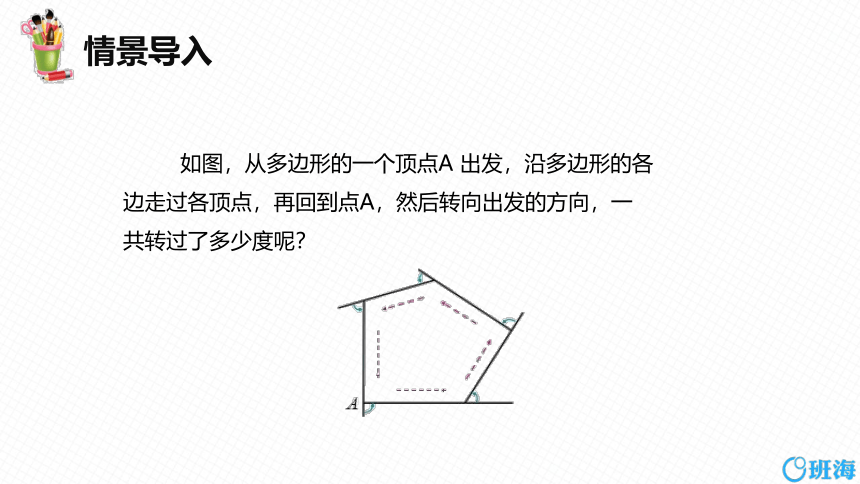
如图,从多边形的一个顶点A 出发,沿多边形的各
边走过各顶点,再回到点A,然后转向出发的方向,一
共转过了多少度呢?
新课精讲
探索新知
1
知识点
多边形的内角和
思考
我们知道,三角形的内角和等于180°,正方形、长方形的内角和都 等于360°.那么,任意一个四边形的内角和是否也等于360°呢?你能利用 三角形内角和定理证明四边形的内角和等于360°吗?
探索新知
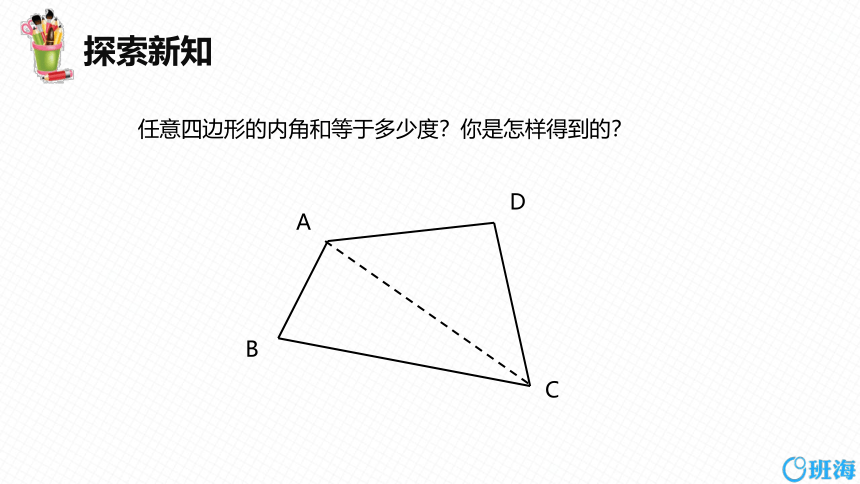
任意四边形的内角和等于多少度?你是怎样得到的?
A
B
C
D
探索新知
A
B
C
D
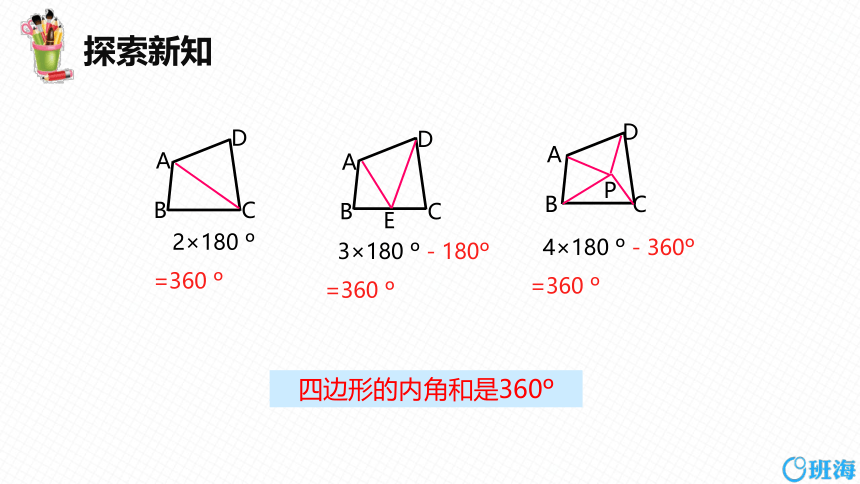
2×180
=360
4×180 -360
=360
四边形的内角和是360
3×180 -180
=360
A
B
C
D
A
B
C
D
E
P
探索新知
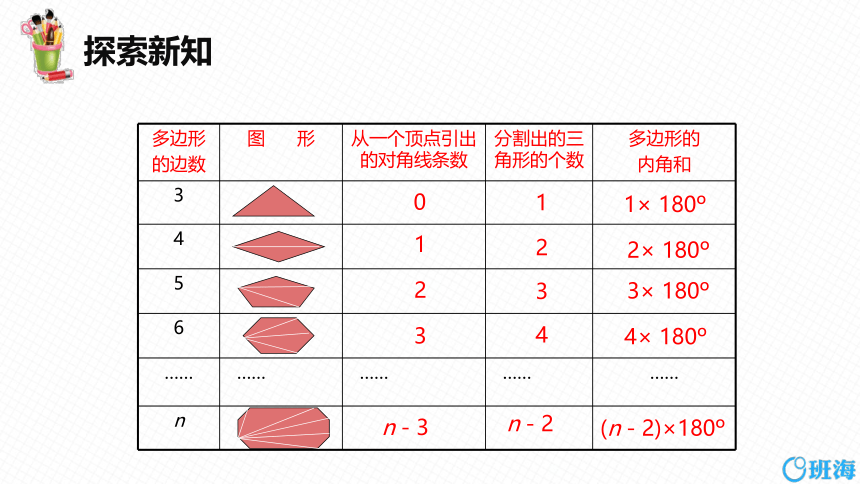
多边形 的边数 图 形 从一个顶点引出的对角线条数 分割出的三角形的个数 多边形的
内角和
3
4
5
6
…… …… …… …… ……
n
(n-2)×180
4× 180
2× 180
3× 180
1× 180
0
1
1
2
2
3
3
4
n-3
n-2
探索新知
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边形内角和公式吗?
探索新知
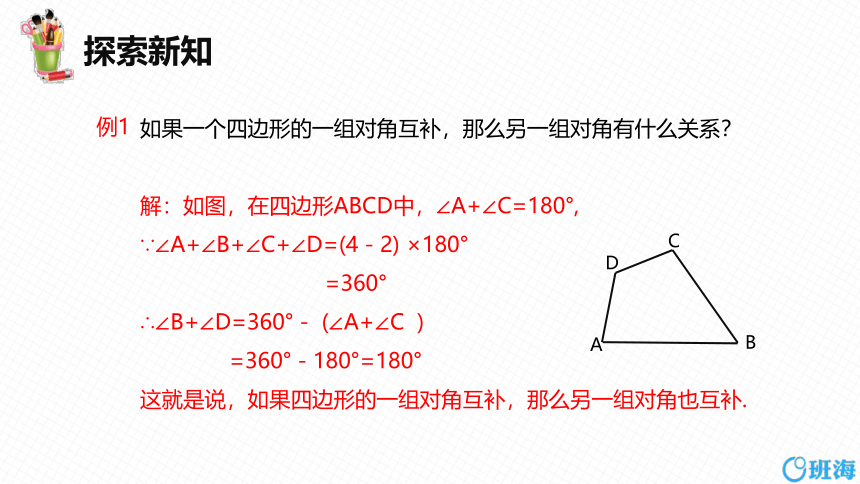
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,在四边形ABCD中,∠A+∠C=180°,
∵∠A+∠B+∠C+∠D=(4-2) ×180°
=360°
∴∠B+∠D=360°- (∠A+∠C )
=360°-180°=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
例1
A
B
C
D
探索新知
若一个多边形的内角和是1260°,则这个多边形的边数是___.
设这个多边形的边数为n,由题意知,
(n-2)×180°=1260°,解得n=9.
例2
导引:
9
探索新知
(1)已知多边形的内角和求边数n的方法:根据多边形内角和公式
列方程:(n-2)×180°=内角和,解方程求出n,即得多边形
的边数;
(2)已知正多边形每个内角的度数k求边数n的方法:根据多边形
内角和公式列方程:(n-2)×180°=kn,解方程求出n,即
得多边形的边数.
总 结
典题精讲
1.一个多边形的各内角都等于120°,它是几边形?
2.已知正多边形的每个内角都是156°,求这个多边形的边数.
解:设这个多边形的边数为n,则(n-2)×180°=n×120°,
解得n=6.所以它是六边形.
解:设这个多边形的边数为n,由题意得(n-2)×180°=
156°×n,解得n=15,即这个多边形的边数为15.
典题精讲
4.一个多边形的每个内角均为120°,则这个多边形是( )
A.四边形 B.五边形
C.六边形 D.七边形
C
3.一个多边形的内角和是360°,这个多边形是( )
A.三角形 B.四边形
C.六边形 D.不能确定
B
探索新知
问题1 我们知道,三角形的内角和是180°,三角形的外角和是360°.得出三角形的外角和是360°有多种方法.如图,你
能说说怎样由外角与
相邻内角互补的关系
得出这个结论吗?
2
知识点
三角形的外角和
A
B
C
D
E
F
1
2
3
探索新知
由 ∠1+∠BAE=180°,∠2 + ∠CBF=180°,
∠3 + ∠ACD=180°,
得 ∠1+∠2+∠3+∠BAE+∠CBF+∠ACD =540°.
由 ∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD
=540°-180°
=360°.
探索新知
问题2 如图,你能仿照上面的方法求四边形的外角和吗?
A
B
C
1
2
3
D
4
探索新知
由 ∠BAD +∠1 =180°,
∠ABC +∠2 =180°,
∠BCD +∠3 =180°,
∠ADC +∠4 =180°,
得∠BAD + ∠1 + ∠ABC +∠2 +∠BCD +∠3 +∠ADC+∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,
得∠1 +∠2 +∠3 +∠4 =180°×4 -180°×2 =360°.
探索新知
问题3 五边形的外角和等于多少度?六边形呢?仿照上面的
方法试一试.
类比求三角形、四边形的外角和的方法求出五边形的外角和是360°,六边形的外角和是360°(解答过程略).
探索新知
如图,在六边形的每个顶点处各取一个外角,这些外角的 和叫做六边形的外角和.六边形的外角和等于多少?
例3
A
B
C
D
E
F
1
2
3
4
5
6
分析:(1)任何一个外角同与它相邻
的内角有什么关系?
(2)六边形的6个外角加上与它们相邻
的内角,所得总和是多少?
(3)上述总和与六边形的内角和、外角
和有 什么关系?
联系这些问题,考虑外角和的求法.
探索新知
解:六边形的任何一个外角加上与它相邻的内角都等于180°.因此六边形 的6个外角加上与它们相邻的内角,所得总和等于6×180°.这个总和就是六边形的外角和加上内角和.所以外角和等于总和减去内角和,即外角和等于:
6×180°- (6 - 2) × 180°=2×180 ° =360 °.
探索新知
思考:
如果将例2中六边形换为n边形(n是不小于3的
任意整数),可以得到同样结果吗?
探索新知
由上面的思考可以得到:多边形的外角和等于360°.
归 纳
探索新知
你也可以像以下这样理解为什么多边形的外角和等于360°.
如图11.3-12,从多边形的一个顶点A出发, 沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.
在行程中所转的各个角的和, 就
是多边形的外角和.由于走了一周,
所转的各个角的和等于一个周角,
所以多边形的外角和等 于 360°.
图 11.3-12
探索新知
已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数.
导引:由四边形外角和定理和各外角之间的比例关系可求出各外角.
解:设四边形的最小外角为x°,则其他三个外角分别为2x°,
3x°,4x°.根据四边形外角和等于360°,得x°+2x°+3x°+4x°=360°.
所以x°=36°,2x°=72°,3x°=108°,4x°=144°.
所以四边形各外角的度数分别为36°,72°,108°,144°.
例4
探索新知
(1)用多边形外角和定理求内(外)角或求正多边形的边数,一般可
利用方程思想通过列方程解决,都是列出外角和的字母表达式:
各个外角的和(如本例)或边数×正多边形每个外角的度数,再
说明它们等于360°,即可求出;
(2)由于多边形的外角和等于360°,因此有些正多边形的内角问
题也可以转化为外角问题来解决.
总 结
学以致用
小试牛刀
1.一般地,从n边形的一个顶点出发,可以作________条对角线,它们
将n边形分为________ 个三角形,因此n边形的内角和是个三角形的
内角的和,即n边形内角和等于_________________.
(n-3)
(n-2)
(n-2)×180°
2.多边形的外角和等于________;它与边数的多少________.由此可知,
任何多边形不可能有_____个或_______个以上的外角为钝角,也就是
说任何多边形不可能有________个或________个以上的内角为锐角.
360°
无关
4
4
4
4
小试牛刀
3.六边形的内角和是( )
A.540° B.720° C.900° D.1 080°
B
4.若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12 C.16 D.18
B
小试牛刀
5.已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )
A.8 B.9 C.10 D.11
C
6.一个多边形的内角和比外角和的2倍多180°,则该多边形的对角线的
条数是( )
A.12 B.13 C.14 D.15
C
小试牛刀
7.一个多边形截去一个角,形成一个新多边形,新多边形的
内角和为2520°.原多边形的边数是多少?
解:2520°÷180°+2=16,
所以新多边形为十六边形.
故原多边形的边数为15,16或17.
小试牛刀
8.一个同学在进行多边形的内角和计算时,求得的内角和为1 125°,
当发现错了以后,重新检查,发现少算了一个内角.这个内角是
多少度?他求的是几边形的内角和?
解:设此多边形的内角和为x°,则有:
1125因为x°为多边形的内角和,
所以它应为180°的整数倍.
所以x=180×7=1260.
所以7+2=9,1260°-1125°=135°.
因此这个内角是135°,他求的是九边形的内角和.
小试牛刀
9.在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,求∠C的度数;
解:∵∠A+∠B+∠C+∠D=360°,
∠B=∠C,
∴∠B=∠C=(360°-∠A-∠D)÷2=70°.
小试牛刀
(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数;
∵BE∥AD,
∴∠BEC=∠D=80°,∠ABE+∠A=180°.
∴∠ABE=180°-∠A=180°-140°=40°.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
小试牛刀
(3)如图③,若∠ABC和∠BCD的平分线交于点E,求∠BEC的度数.
∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D
=360°-140°-80°=140°.
∵∠ABC和∠BCD的平分线交于点E,
∴∠EBC= ∠ABC,∠BCE= ∠BCD.
∴∠E=180°-∠EBC-∠BCE=180°- (∠ABC+∠BCD)
=180°- ×140°=110°.
课堂小结
课堂小结
n边形的内角和:
n边形内角和=(n一2)×180°
n边形的外角和:
多边形的外角和等于360°
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
11.3.2 多边形
的内角和
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图,从多边形的一个顶点A 出发,沿多边形的各
边走过各顶点,再回到点A,然后转向出发的方向,一
共转过了多少度呢?
新课精讲
探索新知
1
知识点
多边形的内角和
思考
我们知道,三角形的内角和等于180°,正方形、长方形的内角和都 等于360°.那么,任意一个四边形的内角和是否也等于360°呢?你能利用 三角形内角和定理证明四边形的内角和等于360°吗?
探索新知
任意四边形的内角和等于多少度?你是怎样得到的?
A
B
C
D
探索新知
A
B
C
D
2×180
=360
4×180 -360
=360
四边形的内角和是360
3×180 -180
=360
A
B
C
D
A
B
C
D
E
P
探索新知
多边形 的边数 图 形 从一个顶点引出的对角线条数 分割出的三角形的个数 多边形的
内角和
3
4
5
6
…… …… …… …… ……
n
(n-2)×180
4× 180
2× 180
3× 180
1× 180
0
1
1
2
2
3
3
4
n-3
n-2
探索新知
一般地,从n边形的一个顶点出发,可以作(n - 3)条对角线,它们将n边形分为(n - 2)个三角形,n边形的内角和等于180°×(n - 2).
把一个多边形分成几个三角形,还有其他分法吗?由新的分法,能得出多边形内角和公式吗?
探索新知
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,在四边形ABCD中,∠A+∠C=180°,
∵∠A+∠B+∠C+∠D=(4-2) ×180°
=360°
∴∠B+∠D=360°- (∠A+∠C )
=360°-180°=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补.
例1
A
B
C
D
探索新知
若一个多边形的内角和是1260°,则这个多边形的边数是___.
设这个多边形的边数为n,由题意知,
(n-2)×180°=1260°,解得n=9.
例2
导引:
9
探索新知
(1)已知多边形的内角和求边数n的方法:根据多边形内角和公式
列方程:(n-2)×180°=内角和,解方程求出n,即得多边形
的边数;
(2)已知正多边形每个内角的度数k求边数n的方法:根据多边形
内角和公式列方程:(n-2)×180°=kn,解方程求出n,即
得多边形的边数.
总 结
典题精讲
1.一个多边形的各内角都等于120°,它是几边形?
2.已知正多边形的每个内角都是156°,求这个多边形的边数.
解:设这个多边形的边数为n,则(n-2)×180°=n×120°,
解得n=6.所以它是六边形.
解:设这个多边形的边数为n,由题意得(n-2)×180°=
156°×n,解得n=15,即这个多边形的边数为15.
典题精讲
4.一个多边形的每个内角均为120°,则这个多边形是( )
A.四边形 B.五边形
C.六边形 D.七边形
C
3.一个多边形的内角和是360°,这个多边形是( )
A.三角形 B.四边形
C.六边形 D.不能确定
B
探索新知
问题1 我们知道,三角形的内角和是180°,三角形的外角和是360°.得出三角形的外角和是360°有多种方法.如图,你
能说说怎样由外角与
相邻内角互补的关系
得出这个结论吗?
2
知识点
三角形的外角和
A
B
C
D
E
F
1
2
3
探索新知
由 ∠1+∠BAE=180°,∠2 + ∠CBF=180°,
∠3 + ∠ACD=180°,
得 ∠1+∠2+∠3+∠BAE+∠CBF+∠ACD =540°.
由 ∠1+∠2+∠3=180°,得
∠BAE+∠CBF+∠ACD
=540°-180°
=360°.
探索新知
问题2 如图,你能仿照上面的方法求四边形的外角和吗?
A
B
C
1
2
3
D
4
探索新知
由 ∠BAD +∠1 =180°,
∠ABC +∠2 =180°,
∠BCD +∠3 =180°,
∠ADC +∠4 =180°,
得∠BAD + ∠1 + ∠ABC +∠2 +∠BCD +∠3 +∠ADC+∠4 =180°×4.
由∠BAD +∠ABC +∠BCD +∠ADC =180°×2,
得∠1 +∠2 +∠3 +∠4 =180°×4 -180°×2 =360°.
探索新知
问题3 五边形的外角和等于多少度?六边形呢?仿照上面的
方法试一试.
类比求三角形、四边形的外角和的方法求出五边形的外角和是360°,六边形的外角和是360°(解答过程略).
探索新知
如图,在六边形的每个顶点处各取一个外角,这些外角的 和叫做六边形的外角和.六边形的外角和等于多少?
例3
A
B
C
D
E
F
1
2
3
4
5
6
分析:(1)任何一个外角同与它相邻
的内角有什么关系?
(2)六边形的6个外角加上与它们相邻
的内角,所得总和是多少?
(3)上述总和与六边形的内角和、外角
和有 什么关系?
联系这些问题,考虑外角和的求法.
探索新知
解:六边形的任何一个外角加上与它相邻的内角都等于180°.因此六边形 的6个外角加上与它们相邻的内角,所得总和等于6×180°.这个总和就是六边形的外角和加上内角和.所以外角和等于总和减去内角和,即外角和等于:
6×180°- (6 - 2) × 180°=2×180 ° =360 °.
探索新知
思考:
如果将例2中六边形换为n边形(n是不小于3的
任意整数),可以得到同样结果吗?
探索新知
由上面的思考可以得到:多边形的外角和等于360°.
归 纳
探索新知
你也可以像以下这样理解为什么多边形的外角和等于360°.
如图11.3-12,从多边形的一个顶点A出发, 沿多边形的各边走过各顶点,再回到点A,然后转向出发时的方向.
在行程中所转的各个角的和, 就
是多边形的外角和.由于走了一周,
所转的各个角的和等于一个周角,
所以多边形的外角和等 于 360°.
图 11.3-12
探索新知
已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数.
导引:由四边形外角和定理和各外角之间的比例关系可求出各外角.
解:设四边形的最小外角为x°,则其他三个外角分别为2x°,
3x°,4x°.根据四边形外角和等于360°,得x°+2x°+3x°+4x°=360°.
所以x°=36°,2x°=72°,3x°=108°,4x°=144°.
所以四边形各外角的度数分别为36°,72°,108°,144°.
例4
探索新知
(1)用多边形外角和定理求内(外)角或求正多边形的边数,一般可
利用方程思想通过列方程解决,都是列出外角和的字母表达式:
各个外角的和(如本例)或边数×正多边形每个外角的度数,再
说明它们等于360°,即可求出;
(2)由于多边形的外角和等于360°,因此有些正多边形的内角问
题也可以转化为外角问题来解决.
总 结
学以致用
小试牛刀
1.一般地,从n边形的一个顶点出发,可以作________条对角线,它们
将n边形分为________ 个三角形,因此n边形的内角和是个三角形的
内角的和,即n边形内角和等于_________________.
(n-3)
(n-2)
(n-2)×180°
2.多边形的外角和等于________;它与边数的多少________.由此可知,
任何多边形不可能有_____个或_______个以上的外角为钝角,也就是
说任何多边形不可能有________个或________个以上的内角为锐角.
360°
无关
4
4
4
4
小试牛刀
3.六边形的内角和是( )
A.540° B.720° C.900° D.1 080°
B
4.若正多边形的一个内角是150°,则该正多边形的边数是( )
A.6 B.12 C.16 D.18
B
小试牛刀
5.已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )
A.8 B.9 C.10 D.11
C
6.一个多边形的内角和比外角和的2倍多180°,则该多边形的对角线的
条数是( )
A.12 B.13 C.14 D.15
C
小试牛刀
7.一个多边形截去一个角,形成一个新多边形,新多边形的
内角和为2520°.原多边形的边数是多少?
解:2520°÷180°+2=16,
所以新多边形为十六边形.
故原多边形的边数为15,16或17.
小试牛刀
8.一个同学在进行多边形的内角和计算时,求得的内角和为1 125°,
当发现错了以后,重新检查,发现少算了一个内角.这个内角是
多少度?他求的是几边形的内角和?
解:设此多边形的内角和为x°,则有:
1125
所以它应为180°的整数倍.
所以x=180×7=1260.
所以7+2=9,1260°-1125°=135°.
因此这个内角是135°,他求的是九边形的内角和.
小试牛刀
9.在四边形ABCD中,∠A=140°,∠D=80°.
(1)如图①,若∠B=∠C,求∠C的度数;
解:∵∠A+∠B+∠C+∠D=360°,
∠B=∠C,
∴∠B=∠C=(360°-∠A-∠D)÷2=70°.
小试牛刀
(2)如图②,若∠ABC的平分线BE交DC于点E,且BE∥AD,求∠C的度数;
∵BE∥AD,
∴∠BEC=∠D=80°,∠ABE+∠A=180°.
∴∠ABE=180°-∠A=180°-140°=40°.
又∵BE平分∠ABC,
∴∠EBC=∠ABE=40°.
∴∠C=180°-∠EBC-∠BEC=180°-40°-80°=60°.
小试牛刀
(3)如图③,若∠ABC和∠BCD的平分线交于点E,求∠BEC的度数.
∵∠A+∠ABC+∠BCD+∠D=360°,
∴∠ABC+∠BCD=360°-∠A-∠D
=360°-140°-80°=140°.
∵∠ABC和∠BCD的平分线交于点E,
∴∠EBC= ∠ABC,∠BCE= ∠BCD.
∴∠E=180°-∠EBC-∠BCE=180°- (∠ABC+∠BCD)
=180°- ×140°=110°.
课堂小结
课堂小结
n边形的内角和:
n边形内角和=(n一2)×180°
n边形的外角和:
多边形的外角和等于360°
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
